2022年度　長崎県公立高校入試問題過去問【数学】解説

問題ＰＤＦ

大問１（小問集合）

（１）
５－３×（－２）²
＝５－３×４
＝５－12
＝－７

（２）
（√３＋１）²－６/√３
＝４＋２√３－２√３
＝４

（３）
２ｘ（ｘ－１）－３＝ｘ²
２ｘ²－２ｘ－３＝ｘ²
ｘ²－２ｘ－３
＝（ｘ＋１）（ｘ－３）＝０
ｘ＝－１、３

（４）
ａｃｍの紙テープから５ｂｃｍを切ると３ｃｍになった。
ａ－５ｂ＝３

（５）
反比例の比例定数ａは積ｘｙで一定。
ａ＝２×６＝12
ｙ＝12/ｘ

（６）
①：√（－２）²＝√４＝２　〇
②：２乗して９になる数が９の平方根。±３を２乗すると９。〇
③：√16＝４　×
④：（√５）²＝５。２乗すると根号が取れる。〇
③

（７）
当たりくじをひく確率は50本中４本。
1000×４/50＝80本

（８）
半径は等しいから二等辺三角形。
180－36×２＝108°

（９）
回転体は底面が半径２ｃｍの円、高さ３ｃｍの円錐。
２×２×π×３÷３＝４πｃｍ³

（10）

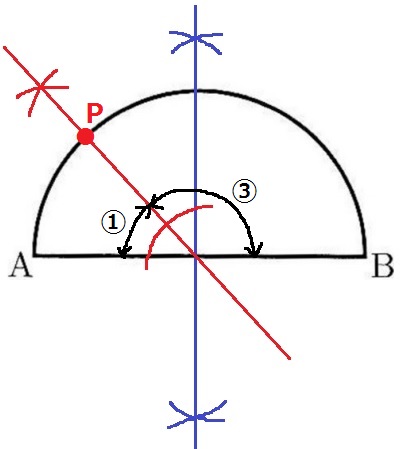
中心角が１：３であれば、弧の長さも１：３になる。
ＡＢの垂直二等分線⇒左側の90°の二等分線。これと半円の弧との交点がＰである。

大問２（データの活用・確率）

問１（１）
ありがたいことに平均点の情報が与えられている。
35人の中央値（メジアン）は18番目の値で８点。
最頻値（モード）は最もあらわれている値で10点。
平均値7.6点＜中央値８点＜最頻値10点
①

（２）
８点未満の生徒の合計点と８点超の生徒の合計点を均すと、平均点の８点になる。
８点未満…３点（８点の５点下）が１人、４点（８点の４点下）が１人…と計算していくと、
－５×１＋（－４）×１＋（－３）×２＋（－２）×３＋（－１）×５＝－26点
８点超…10点（８点の２点上）の生徒だけを計算すると、２×８＝16点
－26＋16＝－10点
９点（８点の１点上）が10人いれば平均点が８点になる→９点は10人
８点の生徒は、35－（１＋１＋２＋３＋５＋10＋８）＝５人

問２（１）
答案では、起こりうるすべての場合をあげ、「同様に確からしい」の用語を用いる。
硬貨Ａと硬貨Ｂを１回投げて起こりうるすべての場合は、
〔表、表〕〔表、裏〕〔裏、表〕〔裏、裏〕の４通りで、
いずれが出ることも同様に確からしい。
２枚とも表は１通りだから、確率は１/４

（２）
すべての場合は、２³＝８通り
硬貨Ａ・Ｂ・Ｃの３枚から１枚の裏を選ぶ。₃Ｃ₁＝３通り
確率は３/８

（３）
全体は、２⁴＝16通り
〔１枚以上が表＝全体－すべて裏〕
４枚すべてが裏になる場合は１通りで確率は１/16
１枚以上が表は、１－１/16＝15/16

大問３（関数）

（１）
ｙ＝ｘ²にｘ＝－２を代入して、
ｙ＝（－２）²＝４

（２）
同様にｘ＝１を代入すると、Ｂ（１、１）
Ａ（－２、４）⇒Ｂ（１、１）
右に３、下に３だから、傾きは－３/３＝－１
Ｂから左に１、上に１移動して切片は２。
ｙ＝－ｘ＋２

（３）

△ＯＡＢは幅３高さ２だから、３×２÷２＝３

（４）①

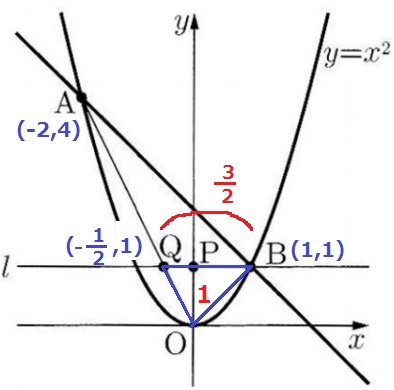
ＡＯ；ｙ＝－２ｘ
これにＱのｙ座標１を代入すると、ｘ＝－１/２
Ｑ（－１/２、１）
△ＯＢＱは底辺ＱＢ＝３/２、高さＰＯ＝１の三角形だから、
３/２×１÷２＝３/４

②
（３）より△ＯＡＢの面積は３なので、２等分した面積が３/２になればいい。

△ＡＱＢの底辺ＱＢと高さの比に注目すると、底辺QB：高さ＝３/２：３＝①：②
直線ｌを上に平行移動させると、どこかで三角形の面積が３/２になる。
そして、平行から底辺：高さの比の①：②は維持される。

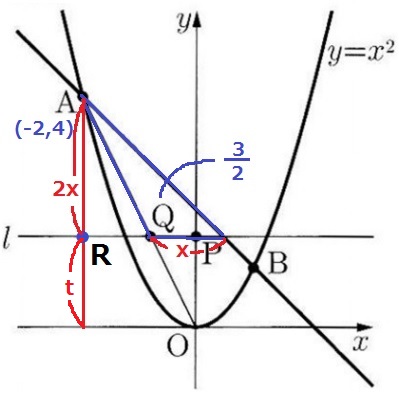
Ａからおろした垂線と直線ｌの交点をＲとする。
面積が３/２になった三角形の底辺をｘとすると、高さはＡＲ＝２ｘ
ｘ×２ｘ÷２＝３/２
ｘ²＝３/２
ｘ＞０より、ｘ＝√６/２
ＡＲの長さは、２ｘ＝√６/２×２＝√６
ｔの値はＲのｙ座標だから、ｔ＝４－√６

大問４（空間図形）

（１）

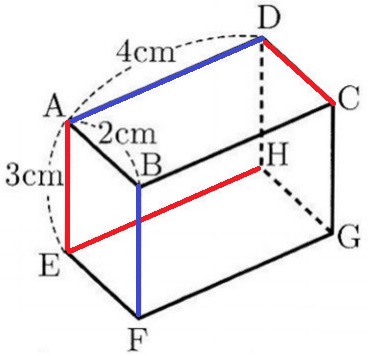
ねじれの位置→平行ではない、かつ延長しても交わらない。
ＡかＤを含む③辺ＣＤと④辺ＡＥは×。
ＡＤ//ＥＨで①辺ＥＨも×。
②辺ＢＦ

（２）
上下の面＋４つの側面
＝２×４×２＋（４＋２）×２×３
＝52ｃｍ²
*側面は展開図になおすと長い長方形。

（３）①

うしろの三角柱に残りの頂点Ａ・Ｂ・Ｄを記入する。
ＤＦ＝６ｃｍ

②

最短距離なので展開図を作成。
△ＰＢＣ∽△ＦＢＥより、ＰＣ＝２×４/10＝４/５ｃｍ

大問５（平面図形）

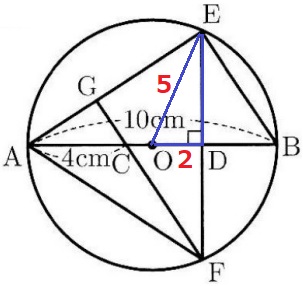
（１）

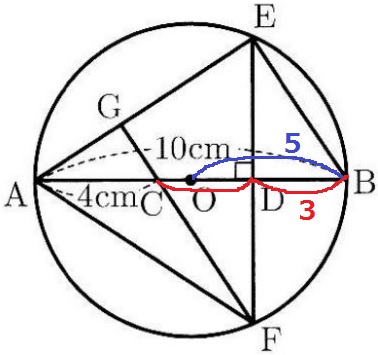
半径ＯＢ＝５ｃｍ
ＣＤ＝（10－４）÷２＝３ｃｍ
ＯＤ＝５－３＝２ｃｍ

（２）

△ＯＤＥで三平方→ＤＥ＝√21ｃｍ

（３）
誘導に従う。

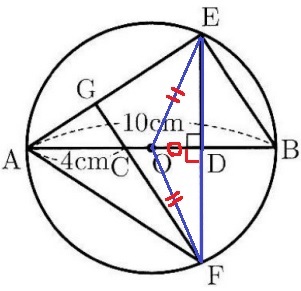
ＯＥ＝ＯＦ、∠ＯＥＤ＝∠ＯＤＦ＝90°、共通辺ＯＤ。
直角三角形の_（ア）斜辺と他の１辺が等しいから、△ＯＥＤ≡△ＯＦＤ

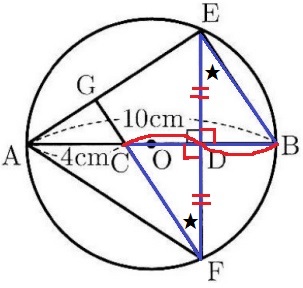
先ほどの合同より対応する辺は等しいので、ＤＥ＝ＤＦ
∠ＢＤＥ＝∠ＣＤＦ＝90°、ＢＤ＝ＣＤとあわせて、
_（イ）２辺とあいだの角が等しいから、△ＢＤＥ≡△ＣＤＦ

対応する角は等しいので、∠ＢＥＤ＝∠ＣＦＤ
_（ウ）錯角が等しいからＥＢ//ＧＦ
ア…斜辺と他の１辺、イ…２辺とあいだの角、ウ…錯角

（４）

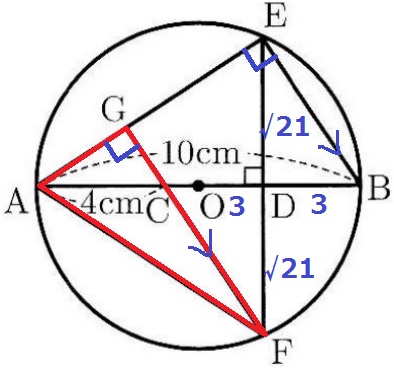
半円の弧に対する円周角は90°だから、∠ＡＥＢ＝90°
ＥＢ//ＧＦの同位角から∠ＡＧＦ＝90°に注目したくなるが、
ＡＧとＧＦの長さを出すのが面倒くさい。
前問の証明からＤＦ＝ＤＥ＝√21ｃｍ
△ＡＣＦの面積が、４×√21÷２＝２√２ｃｍ²とでるので、
あとは上の△ＡＧＣの面積がわかればいい。

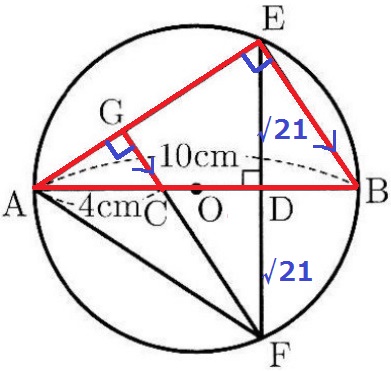
△ＡＥＢの面積は、10×√21÷２＝５√21ｃｍ²
２角が等しく、△ＡＧＣ∽△ＡＥＢ
ＡＣ：ＡＢ＝４：10＝２：５
面積比は相似比の２乗、△ＡＧＣ：△ＡＥＢ＝２²：５²＝④：㉕
△ＡＧＣの面積は、５√21×④/㉕＝４√21/５ｃｍ²
したがって、△ＡＦＧの面積は、４√21/５＋２√21＝14√21/５ｃｍ²

大問６（整数）

（１）
202＋２×４＝210（ア）

もう２回操作を行う。
21＋０×４＝21
２＋１×４＝６（イ）

20回すべて行う必要はないが、６が出てくるまでやり続ける。
2022から操作後の数字を並べてみると、
【210→21→６→24→18→33→15→21→６】
６が初登場するのは３回目。その次が９回目。
周期的にあらわれるので、その次は15回目。
よって、６は３回出現する。（ウ）

最初の１回を除き、【21→６→24→18→33→15…】が繰り返される。
（1000－１）÷６＝166…３
余りの３は【21→６→24】だから24。（エ）
ア…210、イ…６、ウ…３、エ…24

（２）①
十の位がａ、一の位がｂ。
一の位ｂを取り除いた数はａ。これにｂを４倍した数４ｂを加える。
ａ＋４ｂ（オ）

10ａ＋ｂ＝ａ＋４ｂ
これをｂについて解くと、
ｂ＝３ａ（カ）
オ…ａ＋４ｂ、カ…３ａ

②
ａとｂは位の数なので、０＜ａ,ｂ＜９
先ほどのｂ＝３ａから、（ａ、ｂ）＝（１、３）（２、６）（３、９）
よって、13、26、39。
（*いずれも13の倍数である）

（３）
問題文の内容を整理する。

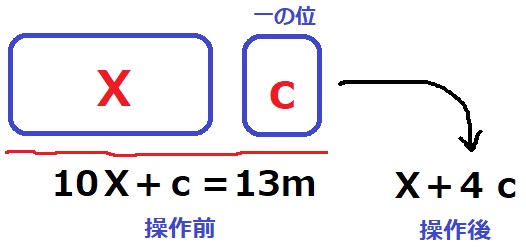
操作前の一の位がｃ、それ以外がＸ。
この数は10Ｘ＋ｃで表され、13の倍数だから10Ｘ＋ｃ＝13ｍ
操作後の数はＸ＋４ｃとなり、これが13の倍数であることを示す。
最終的にＸ＋４ｃを自然数ｍを用いて、13でくくる形にもっていく。

10Ｘ＋ｃ＝13ｍをｃについて解くと、
ｃ＝13ｍ－10Ｘ
これを操作後のｃに代入する。
Ｘ＋４ｃ
＝Ｘ＋４（13ｍ－10Ｘ）
＝52ｍ－39Ｘ
＝13（４ｍ－３Ｘ）
４ｍ－３Ｘは自然数だから、13（４ｍ－３Ｘ）は13の倍数である。
したがって、13の倍数に【操作】を１回行った後の数は13の倍数となる。