2023年度　香川県公立高校入試問題過去問【数学】解説

平均25.3点（前年比；－1.5点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
３＋８÷（－４）
＝３－２
＝１

（２）
６×５/３－５²
＝10－25
＝－15

（３）
（ｘ＋２ｙ）/２＋（４ｘ－ｙ）/６
＝｛３（ｘ＋２ｙ）＋（４ｘ－ｙ）｝/６
＝（３ｘ＋６ｙ＋４ｘ－ｙ）/６
＝（７ｘ＋５ｙ）/６

（４）
√８－√３（√６－√27）　←カッコ内を√３でくくる
＝２√２－√３×√３（√２－√９）
＝２√２－３（√２－３）
＝２√２－３√２＋９
＝９－√２

（５）
（ｘ＋１）（ｘ－３）＋４
＝ｘ²－２ｘ－３＋４
＝ｘ²－２ｘ＋１
＝（ｘ－１）²

（６）
－ｘ²＋ａｘ＋21＝０にｘ＝３を代入。
－３²＋３ａ＋21＝０
３ａ＝－12
ａ＝－４

（７）
12を素因数分解すると、12＝２²×３
２の素因数を２つ、３の素因数を１つ以上含めば12の倍数である。
ウ

大問２（図形）

（１）

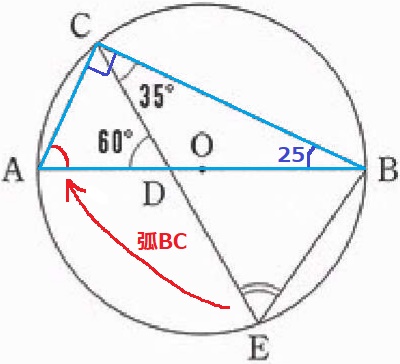
弧ＢＣの円周角より、∠ＢＥＣを∠ＢＡＣに移しておく。
直径ＡＢに対する円周角→∠ＡＣＢ＝90°
△ＢＣＤで外角定理→∠ＣＢＤ＝60－35＝25°
△ＡＢＣの内角から、∠ＢＡＣ＝180－（90＋25）＝65°

（２）ア

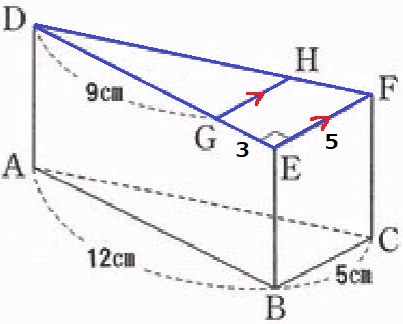
△ＤＧＨ∽△ＤＥＦより、ＧＨ＝５×９/12＝15/４ｃｍ

イ
三角柱の体積を求めるには高さが必要なので、表面積から求める。
側面積＝表面積－底面積×２
＝240－12×５÷２×２＝180ｃｍ²

△ＡＢＣで三平方→辺の比が５：12：13の直角三角形、ＡＣ＝13ｃｍ
側面積を展開すると、横の長さが５＋12＋13＝30ｃｍの長方形になる。
長方形の縦（三角柱の高さ）は、180÷30＝６ｃｍ
体積は、30×６＝180ｃｍ³

（３）

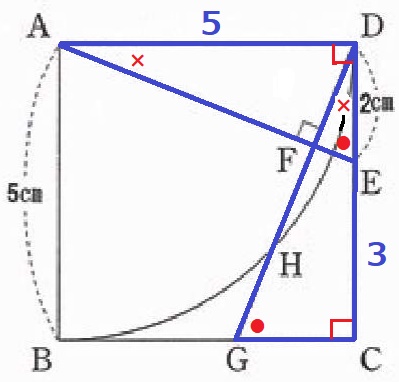
↑この相似には敏感になっておきたい。
△ＡＥＤの内角である∠ＤＡＥ＝×、∠ＡＥＤ＝●とする（×＋●＝90°）。
△ＤＥＦで外角定理、∠ＥＤＦ＝90－●＝×
ＡＤ＝ＤＣ、∠ＡＤＥ＝∠ＤＣＧ、∠ＤＡＥ＝∠ＣＤＧ（×）より、
１辺と両端角が等しく、△ＡＥＤ≡△ＤＧＣ

△ＡＥＤで三平方→ＡＥ＝√29ｃｍ
対応する辺は等しいから、ＤＧ＝√29ｃｍ
いきなりＨＧを求めるのは無理そうなので、ＤＧ－ＤＨから出せないか。

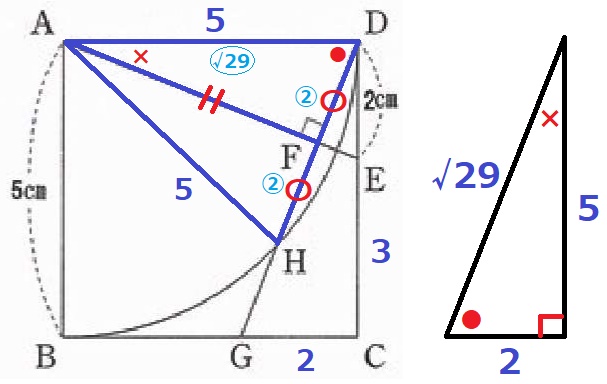
ＡＨに補助線。
△ＡＤＨは等辺５ｃｍの二等辺三角形。
ＡＦ⊥ＤＨ、共通辺ＡＦ→斜辺と他の1辺が等しい直角三角形で△ＡＤＦ≡△ＡＨＦ
ＤＦ＝ＦＨ

△ＡＤＦの内角も●―×―90°だから、辺の比は２：５：√29である。
ＤＨ＝５×④/〇√29＝20√29/29ｃｍ
ＨＧ＝√29－20√29/29＝９√29/29ｃｍ

大問３（小問集合）

（１）
反比例；ｙ＝ａ/ｘ
比例定数ａはｘとｙの積で一定。（ｙ＝ａｘ）
ｙ＝２×５÷３＝10/３

（２）
余事象。
【少なくとも１本は当たり＝全体－２本ともハズレ】
Ａは５本中３本、Ｂは４本中１本がハズレ。
ハズレを２本ひく確率は、３/５×１/４＝３/20
少なくとも１本当たりは、１－３/20＝17/20

（３）
ア：30日間の中央値は15番目と16番目の平均。
　Ａの中央値は200台を超える→少なくとも上位15日は200台超。〇
イ：第１四分位数は下位15日の真ん中、下から８番目。
　Ａ駅とＢ駅の下から８番目が150台。それより下は最小値以外わからない。×
ウ：四分位範囲＝第３四分位数－第１四分位数、箱が長いＣが大きい。〇
エ：最大値はＢが最も大きい。×
ア・ウ

（４）ア
ｙ＝ｘ²において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３/２のとき、最大値ｙ＝９/４
０≦ｙ≦９/４

イ
答案では式を計算を含めて過程を記述する。

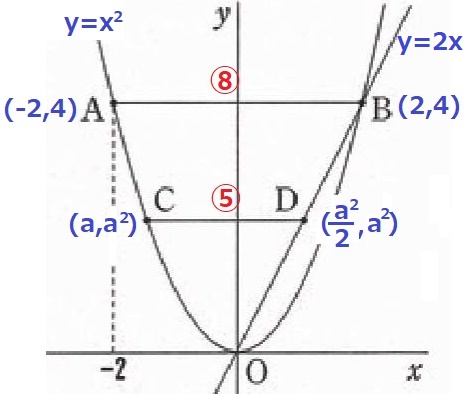
Ｃ（ａ、ａ²）のｘ座標は負なので、ａ＜０
ＯＢ；ｙ＝２ｘにｙ＝ａ²を代入→Ｄ（ａ²/２、ａ²）
ＡＢ＝２－（－２）＝４
ＣＤ＝４×⑤/⑧＝５/２

ＣＤの長さで等式を立てる。
ＣＤ＝ａ²/２－ａ＝５/２
ａ²/２－ａ－５/２＝０　←２倍
ａ²－２ａ－５＝０
解の公式を適用、ｂ＝２ｂ’が使える。
ａ＜０より、ａ＝１－√６

大問４（推論＆方程式）

（１）ア
花子は操作②を終えて、【１、２、７、８】
太郎は操作③を終えて、【５、７、７】
しかし、操作⑤を終えると２人とも同じ値になるらしい。。

太郎の【５、７、７】から【５、７】を取ると５＋７＋２＝14→【７、14】
Ｘ＝７＋14＝21
【７、７】を取ると７＋７＋２＝16→【５、16】
Ｘ＝５＋16＝21で等しくなる。

最初の５枚から２枚とり、２枚を合算して４枚にする。
４枚から２枚とり、２枚の合算に＋１して３枚にする。
３枚から２枚とり、２枚の合算に＋２して２枚にする。
Ｘは残った２枚を合算した値。
ということは、どのような取り方をしても、Ｘは【最初の５枚の和】＋３である。
１＋２＋３＋５＋７＋３＝21
Ｘ＝21

イ

マス目を書いて情報を整理する。
最後の２数の和が62。最初の５つの和は62－３＝59となる。
操作②で取った２枚のうちの１枚が３。

操作③で取った２枚のうちの１枚は１だった→最初の５枚の中に１がある。
操作③終了後の数を★とすると、３枚すべてが★になった。
もし、操作②で合算したカードと１を操作③で合算すると、残りの２枚が★で重複する。
最初のカードは『異なる５つの自然数』なので不適。

ということは、操作③では合算されていないカード同士が合算される。
操作④はどれも★なので、どこで合算してもいい。これでカードの流れが確定した。
★★★＋２＝62
★＝20

こんな感じになる。

残りを埋めると、最初の５枚は１、３、17、18、20。
和を検算すると59である。

（２）ア
ペットボトルは２日間で計280本売れ、１日目は２日目より130本少なかった。
１日目で売れた本数をｘ本とすると、２日目はｘ＋130本。
ｘ＋（ｘ＋130）＝280
ｘ＝75
75本

イ
届けられたアイス…ｘ個
売れたアイスは30％→0.3ｘ個
届けられたドーナツ…ｙ個
すべて売れた→売れたドーナツもｙ個。
『売れたアイスは売れたドーナツよりも34個多かった』
0.3ｘ＝ｙ＋34
ｙ＝0.3ｘ－34

ウ
答案では式と計算を含めて過程も記述する。シンドイ(;´･ω･)
１日目で売れ残り、２日目に売ったアイス…ｘ－0.3ｘ＝0.7ｘ個
２日目に届けられたドーナツ…１日目の３倍だから３ｙ個。
アイスの方が多く（0.7ｘ＞３ｙ）、アイスとドーナツを１個ずつセット販売した。
ドーナツはセット販売のみなので、セットの個数は３ｙセット。
さらに、アイスは個別販売で４個売れた。

２日目終了時の売れ残りはアイス５個とドーナツ３個。
ドーナツはセット販売のみだから３セット売れ残ったことになる。
個別販売で売れ残ったアイスで等式を立てると、

0.7ｘ－３ｙ＝６
これに前問のｙ＝0.3ｘ－34を代入すると、
0.7ｘ－３（0.3ｘ－34）＝６
0.7ｘ－0.9ｘ＋102＝６
0.2ｘ＝96
ｘ＝480
ｙ＝0.3×480－34＝110
ｘ…480　ｙ…110

大問５（図形の証明）

（１）
△ＣＦＧ∽△ＦＩＣの証明

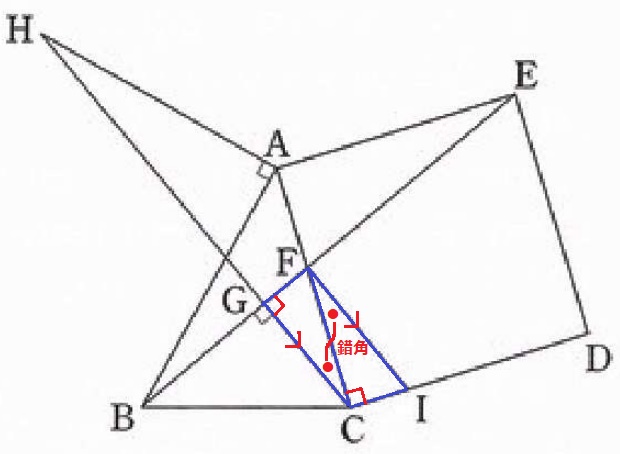
仮定と正方形の内角から、∠ＣＧＦ＝∠ＦＣＩ
ＣＧ//ＩＦの錯角で、∠ＦＣＧ＝∠ＩＦＣ
２角相等で∽。

（２）
ＢＪ＝ＨＫの証明。

ＢＪとＨＫを１辺とする三角形に着目する。
△ＡＢＪと△ＡＨＫが合同であれば、対応する辺からＢＪ＝ＨＫが導ける。
∠ＢＡＪ＝∠ＨＡＫ＝90°
これ以外の情報がないので、別のところで足掛かりをつくるしかない。

↑この形が見えるかどうか。
（問題集に出てくる形式で、Ａを中心に△ＡＢＥを回転させると△ＡＨＣになる）
これらが合同であることを指摘すれば、対応する辺や角を使って証明ができそう。
正方形の辺から、ＡＥ＝ＡＣ
他の等辺が見当たらないので両端角に狙いを絞る。

正方形の内角から、∠ＦＡＥ＝90°
∠ＢＡＥ＝∠ＢＡＦ（×）＋∠ＦＡＥ（90°）＝∠ＢＡＦ（×）＋∠ＨＡＫ（90°）＝∠ＨＡＣ

もう１つの等角は△ＡＦＥと△ＧＦＣに注目する。
∠ＦＡＥ＝∠ＦＧＣ＝90°
対頂角で、∠ＡＦＥ＝∠ＧＦＣ
残りの角は等しいから、∠ＦＥＡ＝∠ＦＣＧ（●）
→∠ＡＥＢ＝∠ＡＣＨ
１辺と両端角が等しいから、△ＡＢＥ≡△ＡＨＣ

対応する辺で、ＡＢ＝ＡＨ
対応する角で、∠ＡＢＪ＝∠ＡＨＫ
１辺と両端角が等しく、△ＡＢＪ≡△ＡＨＫ
対応する辺で、ＢＪ＝ＨＫ