問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
８＋（－４）÷２
＝８－２
＝６
（２）
３ｘ＋ｙ－２（ｘ－３ｙ）
＝３ｘ＋ｙ－２ｘ＋６ｙ
＝ｘ＋７ｙ
（３）
√３＋９/√３
＝√３＋３√３
＝４√３
（４）
反比例はｘｙの積が比例定数ａで一定。
ｙ＝－６×10÷（－３）＝20
（５）
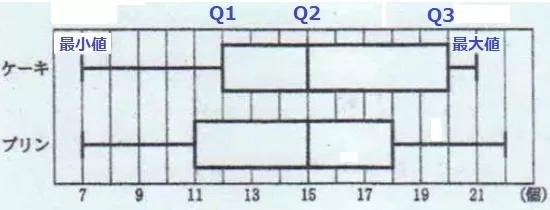
ア：最小値が同じ。最大値はプリンの方が大きい。×
イ：中央値（Q2）は同じ。〇
ウ：四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
箱の長さが大きいのはケーキ。×
エ：31個の中央値は16番目の値。Q3は上位15個の真ん中、上から８番目の値。
ケーキの８番目は20個→19個以上は少なくても８日ある。
プリンの８番目は18個→19個以上は多くても７日しかいない。〇
イ・エ
（６）
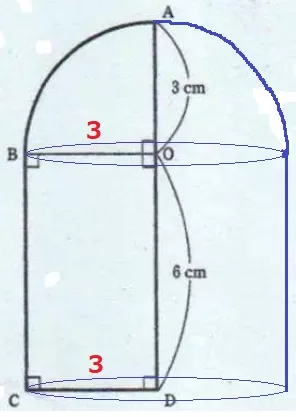
回転体は半径３ｃｍ高さ６ｃｍの円柱と、半径３ｃｍの半球。
【球の体積Ｖ＝４/３πｒ3】
３×３×π×６＋４/３π×３3÷２
＝72πｃｍ3
大問２（方程式）
（１）
ｘ台のテーブル１台に６人ずつ座る。座っている人数は６ｘ人。
８人が座れないので、参加者の人数は６ｘ＋８
（２）ア
１台に７人ずつ座ると、ちょうど座れて２台余る。
→座ったテーブルはｘ－２台。
参加者の人数で等式。
６ｘ＋８＝７（ｘ－２）
ｘ＝22、22台
イ
参加者の人数は、７×（22－２）＝140人
６人テーブルをａ台とすると、７人テーブルは22－ａ台。
６ａ＋７（22－ａ）＝140人
ａ＝14、14台
＠別解＠
すべてが６人テーブルだと、８人座れなかった。
何台かを７人テーブルに切り替える。８人が各テーブルに分かれて、７人テーブルは８台。
６人テーブルは、22－８＝14台
大問３（確率）
（１）
０か３を出すとＡに止まる。
確率は２/５。
（２）
０か３を２回連続で出す。
確率は２/５×２/５＝４/25
（３）
●０周でＡ
和が０→（０、０）の１通り。
●１周でＡ
和が３→（０、３）（１、２）（２、１）（３、０）の４通り。
●２周でＡ
和が６→（２、４）（３、３）（４、２）の３通り。
計８通りだから、確率は８/25
大問４（数量変化）
（１）
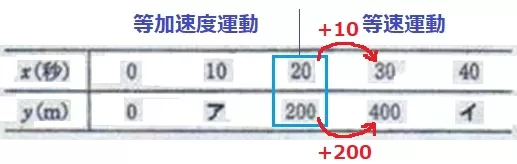
０≦ｘ≦20はｙ＝ａｘ2で表される。
（ｘ、ｙ）＝（20、200）を代入。
200＝400ａ
ａ＝１/２
（２）ア
ｙ＝１/２ｘ2にｘ＝10を代入。
ｙ＝１/２×100＝50
イ
20秒以降は等速運動に変わる。
10秒で200ｍ走る。
ｘ＝40のとき、ｙ＝400＋200＝600
（３）
傾きは、200/10＝20
切片は（20、200）から左に20、下に20×20＝400移動して、
200－400＝－200
ｙ＝20ｘ－200
（４）
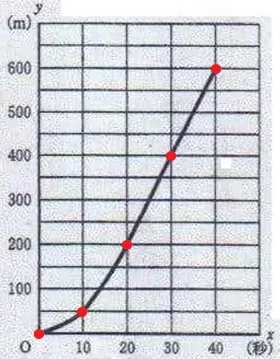
表の格子点を結ぶ。
０≦ｘ≦20はｙ＝ａｘ2（放物線）
20≦ｘ≦40は直線（一次関数）
０≦ｘ≦40のグラフなので40で止めること！
（５）
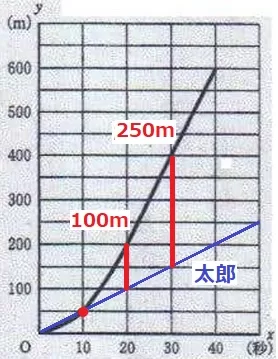
10秒後に電車の先頭部分が太郎に追いつく。
電車の長さは160ｍ。
電車が太郎を完全に追い越すには、先端部分と太郎が160ｍ離れる必要がある。
20秒から電車のグラフは直線になる。
このとき100ｍ離れているので、もう60ｍ離れればいい。
30秒後に250ｍ離れる→10秒間で150ｍ離れる。
60ｍ離れるのは、10×60/150＝４秒後
20＋４＝24秒後
大問５（平面図形）
（１）
△ＡＢＧ≡△ＦＢＥの証明。
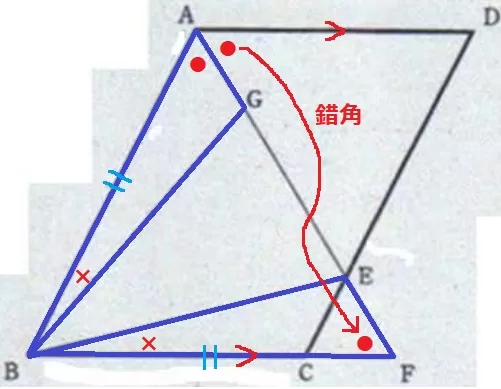
仮定から、∠ＡＢＧ＝∠ＦＢＥ（×）
仮定とＡＤ//ＢＦの錯角で、∠ＢＡＧ＝∠ＢＦＥ（●）
△ＡＢＦは２つの底角が等しい二等辺三角形→ＡＢ＝ＦＢ
１辺と両端角が等しいから合同。
（２）ア
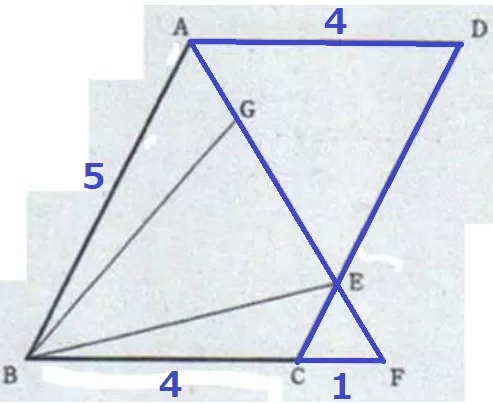
△ＡＢＦは二等辺だから、ＢＦ＝５ｃｍ
ＣＦ＝５－４＝１ｃｍ
平行四辺形の対辺は等しいので、ＡＤ＝４ｃｍ
△ＣＥＦ∽△ＤＥＡより、ＡＥ：ＥＦ＝４：１
ＡＥの長さはＥＦの４倍。
イ
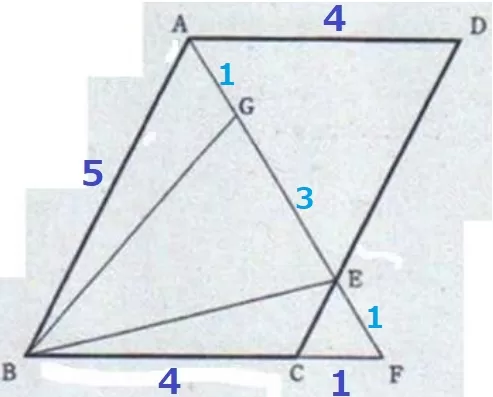
△ＢＥＧの面積比を求めるために、ＡＧ：ＧＥ：ＥＦを出しておく。
ＥＦ＝１とすると、前問よりＡＥ＝４
合同でＡＧ＝１だから、ＧＥ＝４－３＝１
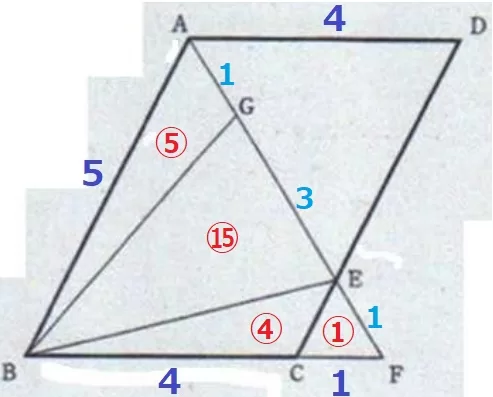
最も面積が小さい△ＣＥＦの面積を①とする。
ＢＣ：ＣＦ＝４：１から、△ＦＢＥ＝⑤
合同で、△ＡＢＧ＝⑤
ＡＧ：ＧＥ＝１：３から、△ＢＥＧ＝⑮
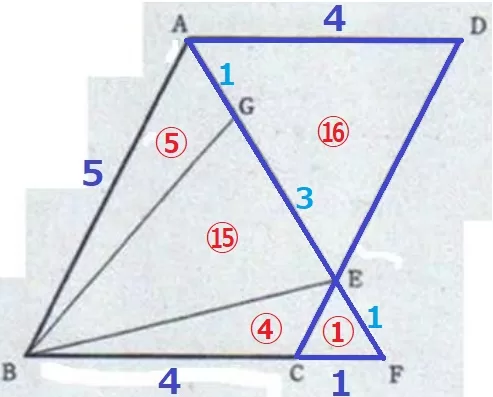
△ＣＥＦ∽△ＤＥＡより、面積比は相似比の２乗→①：⑯
平行四辺形ＡＢＣＤ：△ＢＥＧ＝㊵：⑮＝８：３
平行四辺形ＡＢＣＤの面積は△ＢＥＧの８/３倍。
大問６（総合問題）
（１）
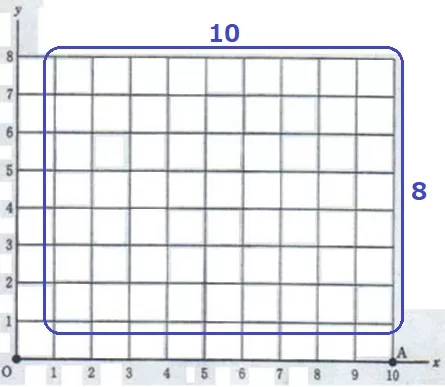
『ｘ座標が１以上10以下の整数、ｙ座標が１以上８以下の整数』
→ｘ軸、ｙ軸上の点は含まない！
青線のエリア内の格子点が答えになる。
10×８＝80通り
（２）
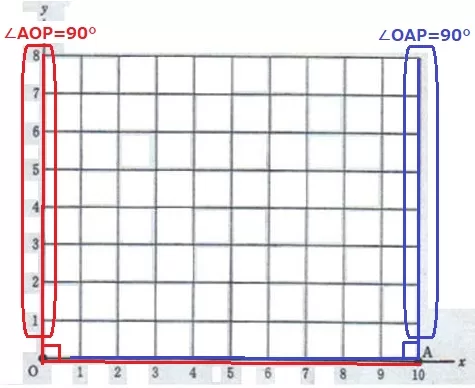
∠ＯＡＰ＝90°→ＰはＡの真上にある。
ｘ＝10の点は８個だから８通り（ア）
∠ＡＯＰ＝90°→ＰはＯの真上にある。
軸上の点は含まないのでＰはない。
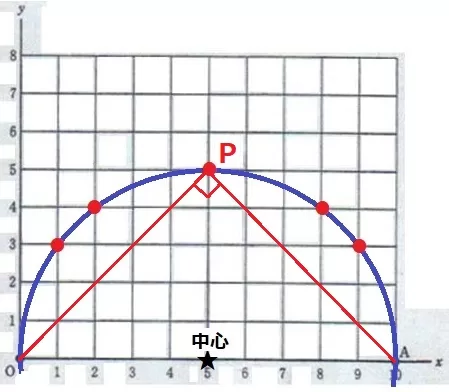
誘導によると、ｘ＝５のときに∠ＯＰＡ＝90°があるという。
ＯＡを斜辺とする直角二等辺三角形を想像すると（５、５）が該当する（イ）
他の点をどう調べるか。
∠ＯＰＡ＝90°を維持する→円周角の定理
直径に対する円周角は90°、直径をＯＡとする円を描く。
円周上の格子点を調べると点（１、３）を含む５個（ウ・エ）
ア…８、イ…５、ウ…３、エ…５
（３）
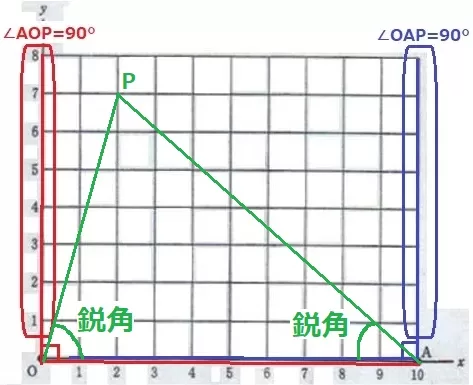
Ｐが１≦ｘ≦９であれば、２つの角は鋭角になる。
この範囲で∠ＯＰＡが鋭角になる格子点を数える。
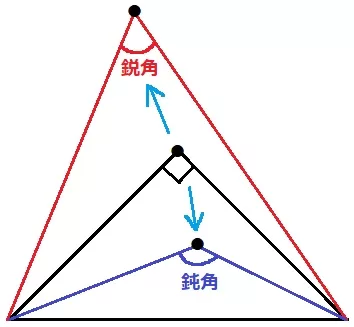
直角三角形の斜辺を固定して直角の頂点を動かす。
上に移動すると鋭角、下に移動すると鈍角になる。
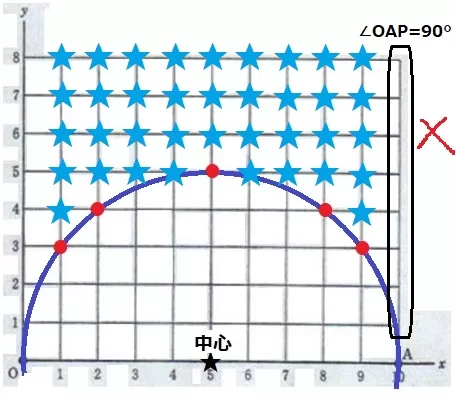
先ほどの半円の弧は∠ＯＰＡ＝90°となるラインなので、
このラインより上側にＰがくると∠ＯＰＡは鋭角になる。
ｙ＝６～８に９個ずつ、ｙ＝５に８個、ｙ＝４に２個なので、
９×３＋８＋２＝37通り
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
おはようございます。お助けマンです。早速の入試問題のご解説、とても嬉しく思います。ありがとうございます。先生の解答・解説は、とても説得力があり、本当に素晴らしいと思います。ここで、大問4の（5）と、大問6の（5）の別解を示したいと思います。
[大問4の（5）］先生のグラフで、太郎さんのグラフの式は、ｙ=5xですね。電車は、160m進むので、電車と太郎さんの差は、160mなので、20x−200−5x=160より、
15x=360、よってx=24、答え 24秒後。
[大問6の（3）］（1）より、三角形の総数は80個である。直角三角形は、先生のご解答のように、（２）の①より8個、（２)の③のエより5個。合わせると直角三角形は、8＋5=13個。半径5の半円内は、鈍角三角形は30個である。鋭角三角形=三角形の総数−直角三角形−鈍角三角形=80−13−30=80−43=37よって答えは、37通りである。
以上ですが、先生のご解答・ご解説以外の別解のご確認をいただけますと嬉しく思います。先生のご教示がいただけますと、嬉しく思います。
今回は、とてもお忙しい中、無理を言いまして、すみませんでした。とても勉強になり、感謝しています。これからも宜しくお願いします。お助けマンより。ならふき
コメントありがとうございます。
読んでくださるだけでこちらも感謝です。私はそんなに大それた者ではありませんので恐縮です。
独りだと思考が寄ってしまうので、お助けマンさんの別解はありがたいです。
●大問４（５）
高校受験の解説ではお助けマンさんの解法がベストです。
私の解説は中学受験の影響を受けており、とくにグラフ問題では別のやり方をよくします。
直線の数式をきちんと求めるのが数学の基本姿勢なので、本当は良くないかもしれませんが書いちゃってます(^^;
●大問６（３）
最後の数え上げは余事象でもいけますね！
ｘ＝５を軸に左右対称なので、半分だけ数えればわりと短時間で求められました。前問の誘導も生きています。
いえいえ(´ω`)無理してませんよ！遅かれ早かれ解説は書く予定でした。
コメントを寄せて頂いてとても励みになります。こちらこそよろしくお願いします。
こんばんは。先ほどは、私解法につきまして、コメントを頂戴でき、感謝しています。特に、大問4の（5）の解法につきまして、お褒めのお言葉、とても嬉しく思います。サボ先生の解法もとても素晴らしく、私も中学入試を受ける児童に教えた経験からも、とても良く分かります。私の場合、良く比例式を立てて、解く事が多いです。今回の問題ですと、10秒間で150m離れるので、60m離れるのは、10:150=□:60よって□=10✕60÷150=4 20＋4=24よって、答えは、24秒後。
勿論サボ先生もこの比例式より、答えを導かれたと思います。このように、数学的に誤りがなければ、解法は自由に考えて解けるかと思います。私は、ここに算数・数学の魅力を感じています。これからも宜しくお願いします。お助けマンより。
コメントありがとうございます。
おっしゃる通りです。グラフ問題は変化の仕方に注目して比例でよく解きます。
市でそのような取り組みがあるのですね( ﾟДﾟ)
そちらで講師を務めていらしたとは凄い！
体調を崩されないよう、お気をつけて下さい。陰ながら応援しております。
こんにちは。早速のサボ先生からのメール、とても嬉しく思います。そして、私の別解に対しましても、過分なるご教示を賜わり、とても有り難く存じます。素晴らしい先生の解答・解説を拝読させていただき、これからも頑張っていきたいと思います。
また、私は、4月から、各務原市教委委員会の主催の「地域未来塾・無償塾=ららら学習室」の講師で、頑張っていきたいと思います。昨年度は、喘息を発症し、一年間、ららら学習室をお休みしました。これからは、中学生の学習指導にも励みたいと思います。これからも宜しくお願いします。お助けマンより。