2020年度　新潟県公立高校入試問題過去問【数学】解説

平均45.3点（前年比；＋8.8点）

説明問題が多いです。以下、解答に説明が求められる設問に★をつけています。
問題はコチラ→ＰＤＦファイル

大問１（小問集合１）－75.4％

（１）　97.2％
７×２－９
＝14－９＝５

（２）　92.6％
３（５ａ＋ｂ）＋（７ａ－４ｂ）
＝15ａ＋３ｂ＋７ａ－４ｂ
＝22ａ－ｂ

（３）　92.0％
６ａ²ｂ×ａｂ÷２ｂ²
＝３ａ³

（４）　87.0％
ｘ－４ｙ＝９
２ｘ－ｙ＝４
連立を解く。
ｘ＝１、ｙ＝－２

（５）　89.4％
√24÷√３－√２
＝√８－√２
＝２√２－√２
＝√２

（６）　76.2％
ｘ²＋３ｘ－１＝０
因数分解ができないので解の公式を適用。
ｘ＝（－３±√13）/２

（７）　68.9％
ｘ＝１のとき、ｙ＝３
ｘ＝６のとき、ｙ＝１/２
１/２≦ｙ≦３

（８）　23.9％！

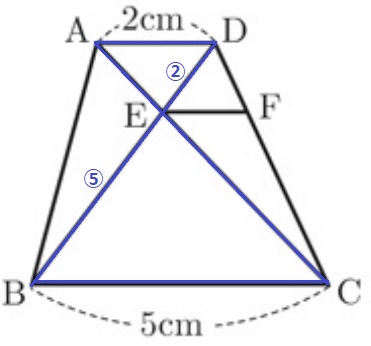
△ＡＤＥ∽△ＣＢＥより、ＤＥ：ＥＢ＝②：⑤
△ＤＥＦ∽△ＤＢＣで、ＥＦ：ＢＣ＝ＤＥ：ＤＢ＝②：⑦
ＥＦ＝５×２/７＝10/７ｃｍ

（９）　47.9％

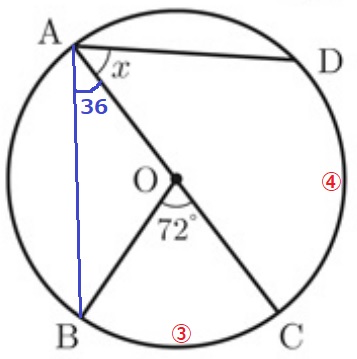
∠ＢＡＣは∠ＢＯＣの円周角→72÷２＝36°
円周角は弧の長さの比例する。
ｘ＝36×４/３＝48°

（10）　79.0％
無作為に取り出した40個のうち、青は７個。
480×７/40＝84個

大問２（小問集合２）－54.2％

（１）★　45.7％
２つのパターンを鉛筆の本数ｙで等式。
ｙ＝４ｘ－８
ｙ＝３ｘ＋12
過不足の処理に気を付けよう！
４ｘ－８＝３ｘ＋12
ｘ＝20
ｙ＝４×20－８＝72
ｘ＝20、ｙ＝７

（２）★　56.5％
５×５＝25なので、26以上の方が少ない。
積が26以上は（５、６）（６、５）（６、６）の３通りだけ。
積が25以下は、６×６－３＝33通り。
確率は33/36＝11/12

（３）①　56.1％
ｙ＝ｘ²に代入→Ａ（－３、９）
Ａ（－３、９）を通る、傾きが－１の直線の式を求める。
Ａから右に３、下に３移動すると切片。９－３＝６
ｙ＝－ｘ＋６

②★　52.6％

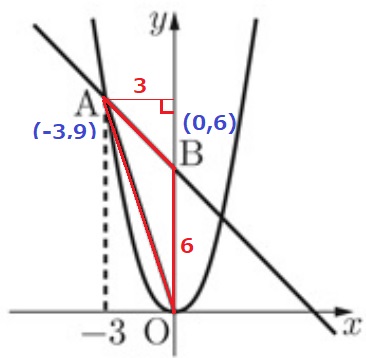
典型問題ゆえミスしたくはない。
辺ＯＢを底辺として、６×３÷２＝９
説明問題でなくても良かったと思うが(;´･ω･)

（４）　60.0％
『２つの点Ａ，Ｂを通る円の中心Ｐ』→ＰはＡＢの垂直二等分線上にある。
これと直線ℓとの交点がＰとなる。

大問３（平面図形）－45.0％

★△ＡＥＦ≡△ＣＥＧの証明１題。

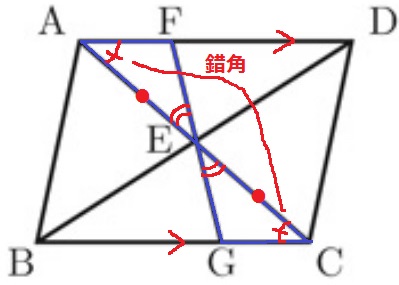
対頂角。ＡＤ//ＢＣから錯角。
平行四辺形の対角線は各々の中点で交わる→ＡＥ＝ＣＥ
以上、１辺と両端角相等で合同。

大問４（数量変化）－26.4％

（１）　41.1％

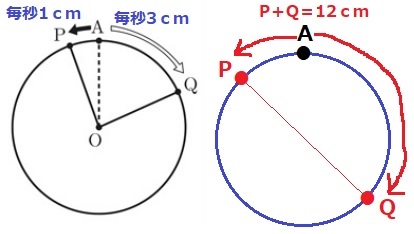
Ｐは反時計回りに秒速１ｃｍ、Ｑは時計回りに秒速３ｃｍ。
ＰＱが円Ｏの直径、すなわち反対側にくるとき、ＰとＱの移動距離の和は半周12ｃｍ。
１秒間にＰとＱは４ｃｍずつ離れていくから、12÷４＝３秒後

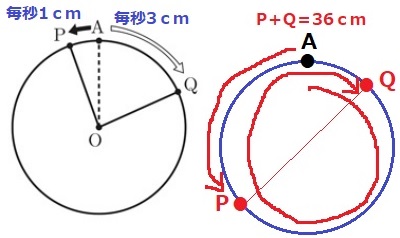
その後、ＰとＱは近づいていき、両者が重なる。
そこから１秒あたり４ｃｍずつ離れていき、再びＰとＱが反対側にくるのは、
ＰとＱの移動距離の和が１周半である36ｃｍのとき。
36÷４＝９秒後
ｘ＝３、９

（２）①　53.3％
ＰとＱが重なるのは、前問の３秒後と９秒後のあいだである６秒後。
計算式でかくと、ＰとＱの移動距離の和が１周24ｃｍだから、24÷４＝６秒後
ｘ＝６

②　11.1％！
ｘ＝３のとき、ＰＱは半周でｙ＝12
ｘ＝６のとき、ＰとＱは重なっているのでｙ＝０
（３、12）と（６、０）を通る直線の式を求める。
12＝３ａ＋ｂ
－)０＝６ａ＋ｂ
12＝－３ａ
ａ＝－４
ｂ＝24
ｙ＝－４ｘ＋24

（３）★　13.3％！
ここも説明いるのか(;`ω´)

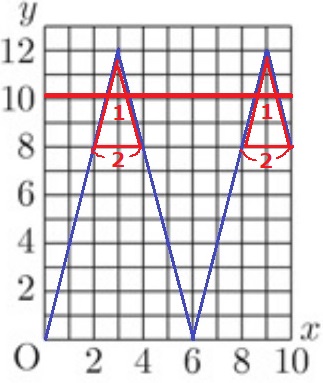
グラフを描写。
ｙ≧10を考えよう。
赤い三角形の∽から、ｙ≧10のときは１＋１＝２秒間。
ｙ≦10は、10－２＝８秒間

大問５（規則）－26.9％

（１）①　41.1％
初問で規則を見つけておきたい。

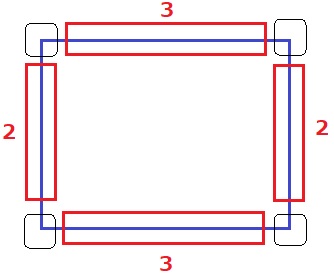
外側に白い辺ができる。四隅（角）は２辺が白なので除く。
ａ＝｛（４－２）＋（５－２）｝×２＝10

②　53.3％
同様。
ａ＝｛（12－２）＋（18－２）｝×２＝52

（２）★　11.1％！

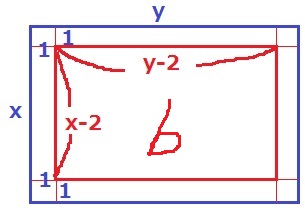
外側から中に１つ進むとｂ。
ｂの縦はｘ－２、横はｙ－２。
ｂ＝（ｘ－２）（ｙ－２）
＝ｘｙ－２ｘ－２ｙ＋４

（３）★　13.3％！
前図より、ａ＝｛（ｘ－２）＋（ｙ－２）｝×２＝２ｘ＋２ｙ－８
ｂ－ａ＝20
ｂ－ａ
＝ｘｙ－２ｘ－２ｙ＋４－（２ｘ＋２ｙ－８）
＝ｘｙ－４ｘ－４ｙ＋12＝20
ｘｙ－４ｘ－４ｙ－８＝０
ｙ＝ｘ＋５を代入。
ｘ（ｘ＋５）－４ｘ－４（ｘ＋５）－８
＝ｘ²－３ｘ－28＝（ｘ＋４）（ｘ－７）＝０
題意よりｘ≧３なので、ｘ＝７
ｙ＝７＋５＝12
ｘ＝７、ｙ＝12

＠別解＠

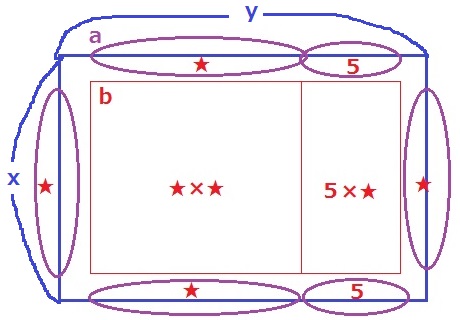
ｘの両端を除き、ｘ－２＝★とします。ｂの縦は★。
ｙはｘより５を大きい⇒ｙ－２はｘ－２より５大きい。ｂの横は★＋５。
ａ＝４×★＋10
ｂ＝★×★＋５×★
ｂ－ａ＝★²＋５★－（４★＋10）＝20
★²＋★－30
＝（★＋６）（★－５）＝０
★＞０より、★＝５
ｘ＝★＋２＝５＋２＝７
ｙ＝７＋５＝12

大問６（空間図形）－18.1％

（１）①　40.4％

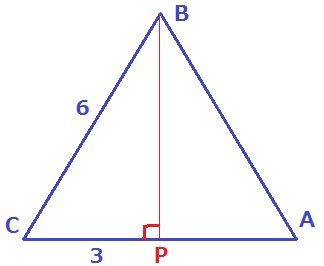
△ＡＢＣは１辺６ｃｍの正三角形。
△ＢＣＰで三平方→辺の比は１：２：√３だから、ＢＰ＝３√３ｃｍ

②　45.0％
６×３√３÷２＝９√３ｃｍ²

（２）★　13.4％！

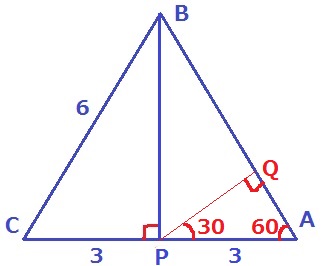
△ＡＰＱの内角は30°－60°－90°で辺の比は１：２：√３。
ＡＱ＝３÷２＝３/２ｃｍ

（３）①★　1.9％!!

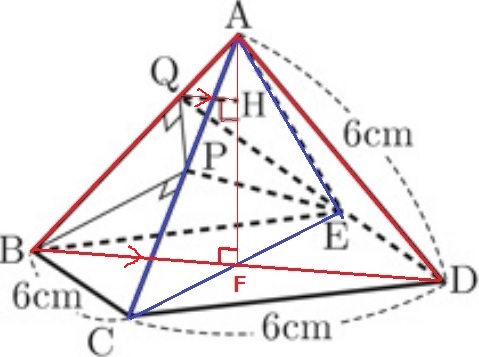
ポイントは△ＡＢＤと△ＡＣＥ！
ＢＤとＣＥは底辺の正方形の対角線なので、２つの三角形はＡＦで直交している。
ＢＤとＣＥの交点をＦとする。△ＡＢＦ⊥△ＡＣＥ
∠ＢＦＡ＝90°
△ＡＰＥは△ＡＣＥ上にある。辺ＡＢ上の点Ｑからひいた垂線もＡＦと交わる。∠ＱＨＡ＝90°
同位角が等しく、ＱＨ//ＢＦ。
△ＡＱＨと△ＡＢＦは相似である。

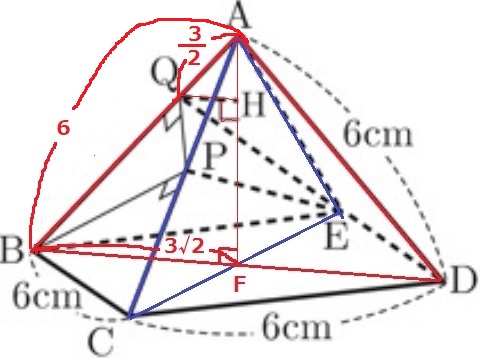
前問より、ＡＱ＝３/２ｃｍ
ＡＱ：ＡＢ＝ＱＨ：ＢＦ＝３/２：６＝１：４
ＱＨ＝３√２×１/４＝３√２/４ｃｍ

②★　0.7％!!!
高さＱＨが出たので、底面である△ＡＰＥの面積さえわかればいい。

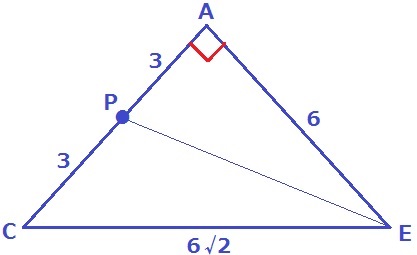
ここも△ＡＣＥで考える。
直角二等辺三角形ＣＤＥ→辺の比が１：１：√２より、ＣＥ＝６√２ｃｍ
△ＡＣＥの３辺の比は、６：６：６√２＝１：１：√２！
すなわち、△ＡＣＥも直角二等辺三角形であり、∠ＰＡＥ＝90°
（正四角錘を対角線で切った断面は直角二等辺三角形）
よって、四面体ＡＰＥＱの体積は、
３×６÷２×３√２/４÷３＝９√２/４ｃｍ³