2023年度　都立高校入試問題過去問【数学】解説

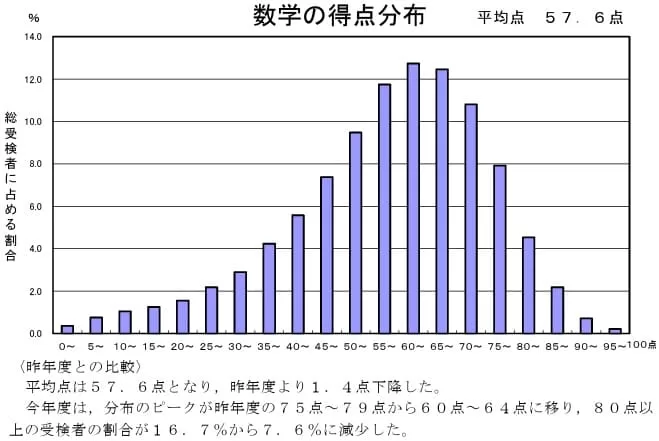
平均57.6点（前年比；－1.4点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）―76.5％

（１）　95.1％
－８＋６²÷９
＝－８＋36÷９
＝－８＋４
＝－４

（２）　77.3％
（７ａ＋ｂ）/５－（４ａ－ｂ）/３
＝｛３（７ａ＋ｂ）－５（４ａ－ｂ）｝/15
＝（21ａ＋３ｂ－20ａ＋５ｂ）/15
＝（ａ＋８ｂ）/15

（３）　73.6％
（√６－１）（２√６＋９）
＝12＋９√６－２√６－９
＝３＋７√６

（４）　90.4％
４（ｘ＋８）＝７ｘ＋５
４ｘ＋32＝７ｘ＋５
３ｘ＝27
ｘ＝９

（５）　87.6％
２ｘ＋３ｙ＝１　…①
８ｘ＋９ｙ＝７　…②
②－①×３で、２ｘ＝４
ｘ＝２
①に代入して、２×２＋３ｙ＝１
ｙ＝－１
ｘ＝２、ｙ＝－１

（６）　72.2％
２ｘ²－３ｘ－６＝０
解の公式を適用して、ｘ＝（３±√57）/４

（７）　71.2％
６個から２個を選ぶ→₆Ｃ₂＝15通り
青は４個。青₁～青₄から２個を選ぶ→₄Ｃ_２＝６通り
確率は、６/15＝２/５
あ…２、い…５

（８）　66.1％

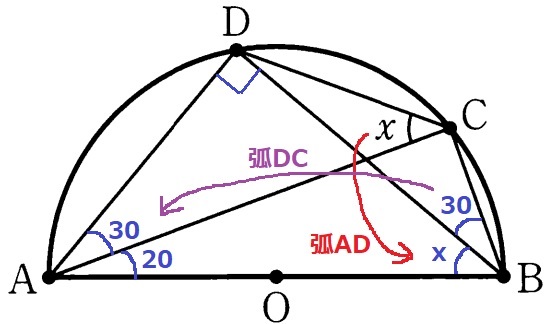
弧ＤＣの円周角、∠ＤＡＣ＝30°
弧ＡＤの円周角、∠ＤＢＡ＝ｘ
直径に対する円周角、∠ＡＤＢ＝90°
△ＡＢＤの内角より、ｘ＝180－（90＋30＋20）＝40°
う…４、え…０
*50°の誤答が多かった。二等辺三角形と誤認したか。

（９）　54.7％

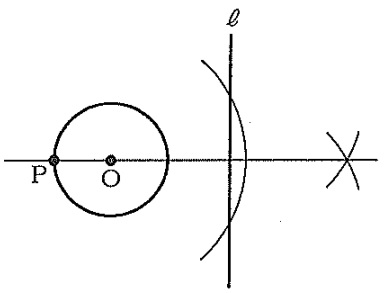
Ｏを通る直線ℓの垂線を引き、ℓの反対側がＰになる。
*誤答では、解答用紙記載の直線ℓを線分とみなして垂直二等分線を作図する者が多かった。
なんじゃそりゃ！

大問２（式の証明）―26.8％

（１）　31.7％！

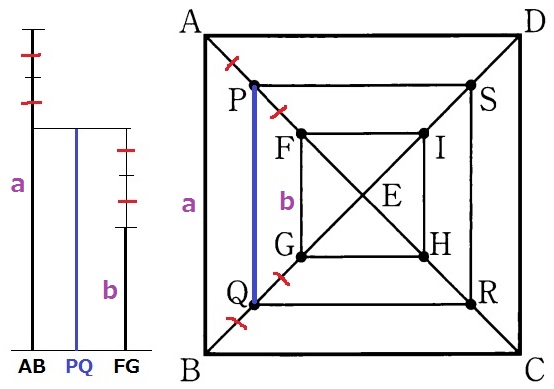
ＡＢとＦＧの長さを均すとＰＱになる。
ＰＱ＝（ａ＋ｂ）/２ｃｍ
正方形ＰＱＲＳの周の長さℓ＝（ａ＋ｂ）/２×４＝２ａ＋２ｂｃｍ
ア

（２）　21.9％！（無答55.3％）

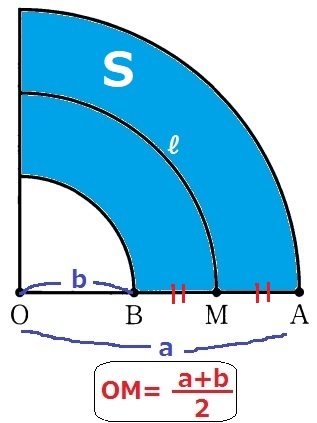
ＯＡとＯＢの平均がＯＭ→ＯＭ＝（ａ＋ｂ）/２
ℓの長さを求める。半径（ａ＋ｂ）/２ｃｍの４分の１円の弧だから、
ℓ＝（ａ＋ｂ）/２×２×π×１/４＝１/４π（ａ＋ｂ）

導出したい式は、【Ｓ＝（ａ－ｂ）ℓ】
右辺のℓに先ほどの値を代入する。
（ａ－ｂ）ℓ＝（ａ－ｂ）×１/４π（ａ＋ｂ）
＝１/４π（ａ＋ｂ）（ａ－ｂ）…①

左辺のＳ（面積）を図から求める。
半径ａｃｍの４分の１円から、半径ｂｃｍの４分の１円を引く。
Ｓ＝１/４πａ²－１/４πｂ²
＝１/４π（ａ²－ｂ²）
＝１/４π（ａ＋ｂ）（ａ－ｂ）…②
①＝②から、Ｓ＝（ａ－ｂ）ℓ
*扇形の面積は文字で立式できても、弧の長さを求める際に半径の立式ができなかった恐れあり。

大問３（関数）―42.1％

（１）　73.7％
Ｐはｙ＝１/２ｘ＋１上の点。これにｙ＝－１を代入する。
－１＝１/２ｘ＋１
ｘ＝－４
エ

（２）　38.6％

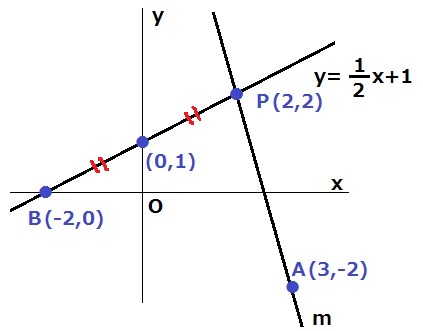
ｙ＝１/２ｘ＋１にｘ＝０を代入→Ｂ（－２、０）
ＢＰの中点は、ｙ＝１/２ｘ＋１の切片（０、１）である。
Ｂから右に２、上に１移動して切片。さらに右に２、上に１移動してＰ（２、２）
Ｐ（２、２）→Ａ（３、－２）
右に１、下に４移動するから、ｍの傾きは－４。
Ｐから左に２、上に８移動して、ｍの切片は２＋８＝10
ｍ；ｙ＝－４ｘ＋10
①…イ、②…エ

（３）　13.8％！（誤答42.9％、無答43.3％）

ＰとＱはｙ軸について線対称。
ＰＱの中点をＭとするとＭはｙ軸上にある。
ＱＭ＝ＭＰより、△ＢＭＱと△ＢＰＭの面積は等しい。
△ＢＰＱの面積が△ＡＰＢの２倍→３つの★の面積が等しい。

Ａを通る直線ℓに平行な線をひき、ｘ軸との交点をＡ’とする。
傾きは１/２だから、Ａから上に２、右に４移動してＡ’（７、０）
△ＢＰＭと△ＰＢＡ’は等積でＭＰ//ＢＡ’から高さ共通。
→底辺共通でＭＰ＝ＢＡ’＝７－（－２）＝９
Ｐのｘ座標は９。

大問４（平面図形）―40.9％

（１）　59.8％

仮定からＡＢ＝ＤＣ
四角形ＡＱＣＤに注目すると、２組の対辺が平行だから平行四辺形。
対辺は等しく、ＡＱ＝ＤＣ（図の水色が同じ長さ）

∠ＡＱＢ＝180－110＝70°
△ＡＢＱは二等辺三角形。その底角と錯角で70°を移動させる。
最後に△ＡＰＤで外角定理→∠ＡＤＰ＝70－ａ°
ウ

（２）①　61.4％
△ＡＳＤ∽△ＣＳＱの証明。

わかりやすい。
対頂角＋ＡＤ//ＢＣの錯角→２角相等で∽。

②　1.7％!!（誤答71.3％、無答27.0％）

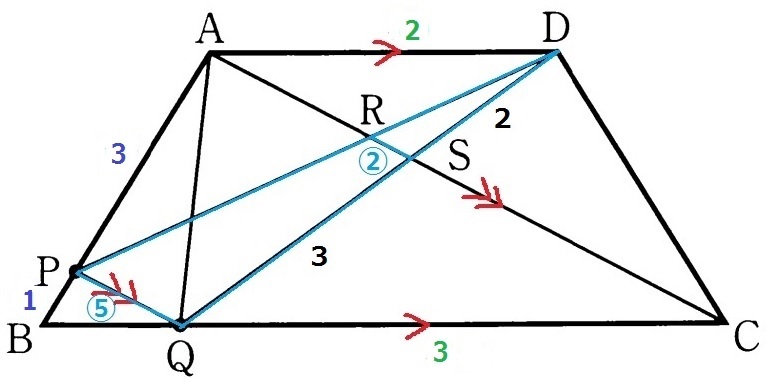
ここも〔問２〕でまとまっているので、前問の相似を疑う。
△ＡＳＤ∽△ＣＳＱから、ＤＳ：ＳＱ＝２：３
ＲＳ//ＰＱより△ＤＲＳ∽△ＤＰＱで、ＲＳ：ＰＱ＝ＤＳ：ＤＱ＝②：⑤

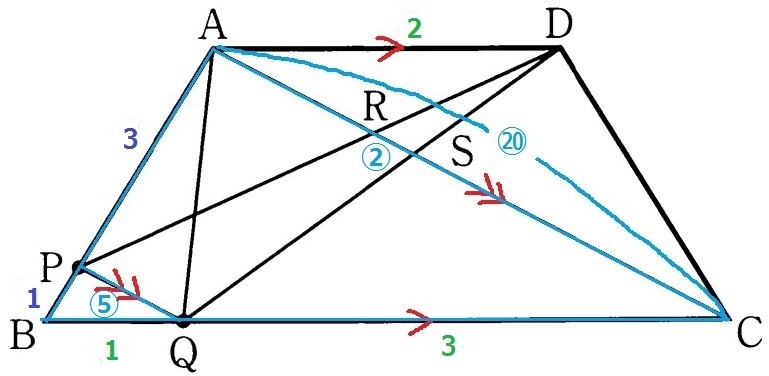
今度は逆方向から相似を捉える。
ＰＱ//ＡＣから△ＢＱＰ∽△ＢＣＡ。
ＢＱ：ＱＣ＝ＢＰ：ＰＡ＝１：３より、ＢＱ＝１
ＡＣ＝ＰＱ×４＝⑤×４＝⑳

比を整理すると、ＲＳ：ＡＣ＝②：⑳＝１：10
△ＤＲＳの面積を①とすると、△ＤＡＣ＝⑩
上底ＡＤ：下底ＢＣ＝２：４から、台形ＡＢＣＤは⑩×６/２＝㉚
したがって、△ＤＲＳは台形ＡＢＣＤの１/30倍。
お…１、か…３、き…０

＠別解＠

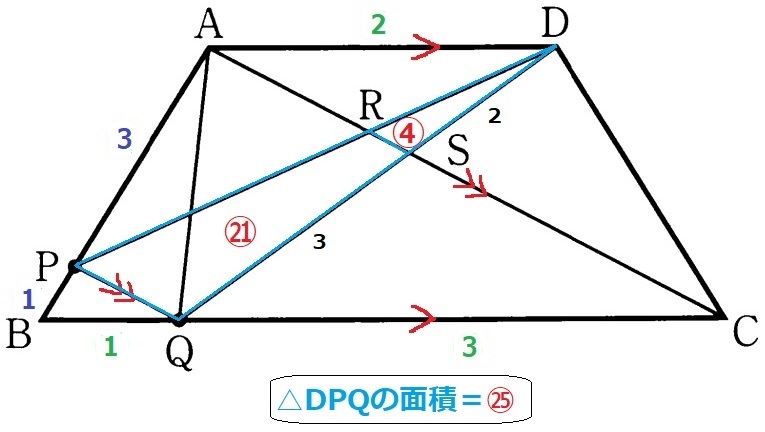
ＤＳ：ＳＱ＝２：３、ＢＱ＝１は先と同様。
面積比は辺の比の２乗→△ＤＲＳ：△ＤＰＱ＝２²：５²＝④：㉕

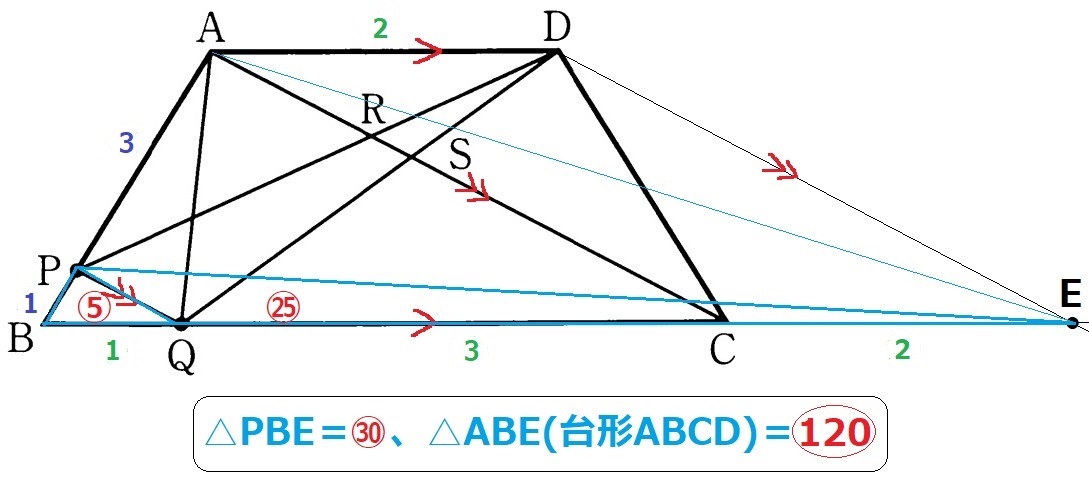
Ｄを通るＡＣに平行な線をひき、ＢＣの延長線との交点をＥとする。
等積変形で△ＡＣＤ＝△ＡＣＥ
台形ＡＢＣＤの面積は△ＡＢＥに相当する。
また、等積変形で△ＤＰＱ＝△ＥＰＱ＝㉕
平行四辺形ＡＣＥＤの対辺は等しく、ＣＥ＝２
ＢＱ：ＱＥ＝１：５から、△ＰＢＥ＝㉚
ＰＢ：ＡＢ＝１：４から、△ＡＢＥ（台形ＡＢＣＤ）＝〇120
したがって、△ＤＲＳは台形ＡＢＣＤの④/〇120＝１/30倍。

大問５（空間図形）―7.8％

（１）　12.5％！（誤答70.8％、無答16.8％）
ＰはＡＢ上にある。

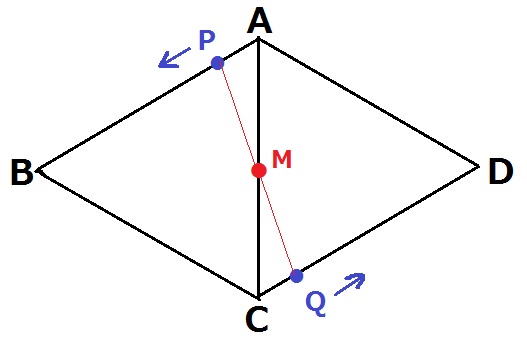
最短距離なので、展開図を作成する。
ＰはＡ→Ｂ→Ｃ、ＱはＣ→Ｄ→Ａを毎秒１ｃｍで移動する。

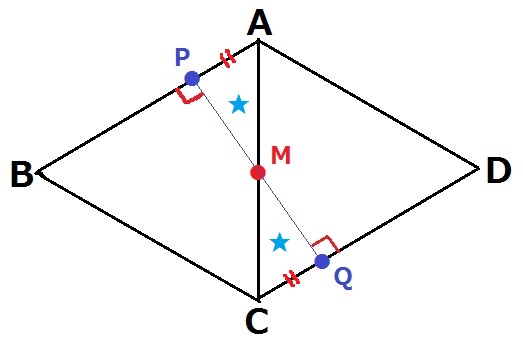
ＭＰ＋ＭＱが最短となるのは、ＰＱが直線になるとき。
ＰとＱは対称的に動くので、２つの三角形★は合同である。

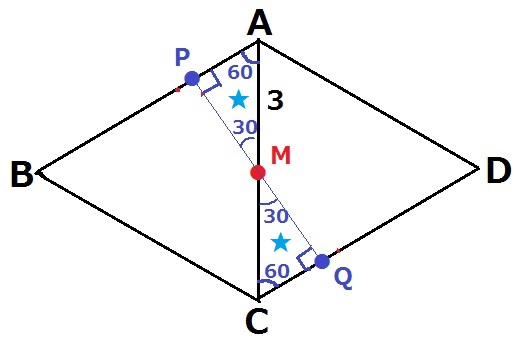
正三角形ＡＢＣの１つの内角より、∠ＭＡＰ＝60°。
ＭはＡＣの中点でＡＭ＝３ｃｍ
△ＡＰＭの内角から辺の比は１：２：√３→ＡＰ＝３/２ｃｍ
Ｐの速さは毎秒１ｃｍなので３/２秒後。
く…３、け…２

＠別解＠

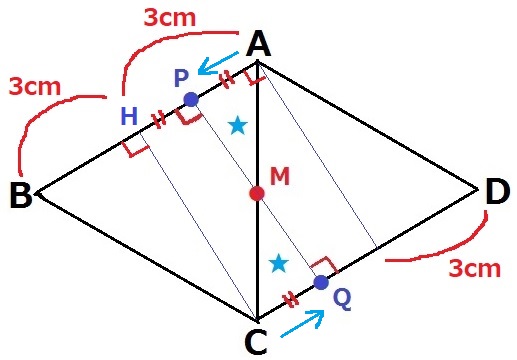
Ｃを通るＡＢの垂線の足をＨとする。
ＨはＡＢの中点だから、ＡＨ＝３ｃｍ
この距離をＰとＱが同じ速さで移動するので、ＡＰ＝３÷２＝３/２ｃｍ
（ＡＨ上で仮にＰはＡから、ＱはＨから出発したとすると、出会うのはＡＨの中点）

（２）　3.2％!!（誤答66.8％、無答30.0％）
“体積比”ではなく”体積”なので、１辺６ｃｍの正四面体の体積を算出する(´Д`||)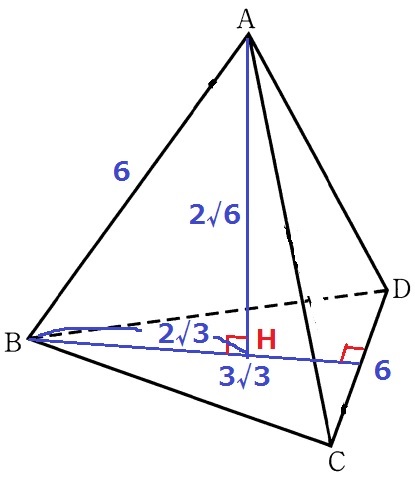
↑こうなる。
Ａからおろした垂線の足であるＨは正三角形ＢＣＤの重心であり、中線を２：１に内分する。
△ＡＢＨで三平方→高さＡＨ＝２√６ｃｍ
正四面体の体積は、６×３√３÷２×２√６÷３＝18√２ｃｍ³

＠余談＠
実は、一発で正四面体の体積を出す公式がある。

１辺がａの四面体の体積…Ｖ＝√２/12ａ³

１辺６ｃｍだと、Ｖ＝√２/12×６³＝18√２ｃｍ³
これを知っているか否かで時間短縮が半端ない。。
理由は１辺をａとして地道に三平方で導出します。
詳しい説明は以下のリンク先からどうぞ。
＞数学切り抜き帳

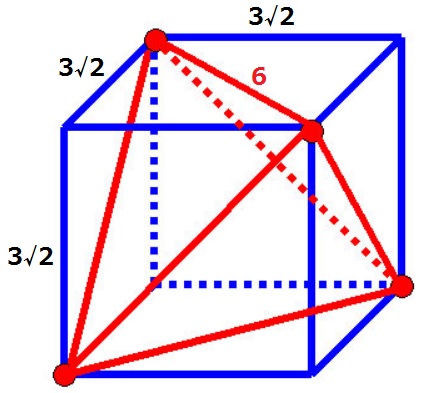
また、正四面体はこのように立方体に収納することができる。
正四面体の１辺は正方形の対角線。１：１：√２から立方体の１辺は３√２ｃｍ。
立方体から４つの三角錐をひけば、真ん中の正四面体になる。
三角錐の底面積は正方形の１/２倍。錘の体積は柱の１/３倍。
立方体の体積を⑥とすると、１つの三角錐の体積は⑥×１/２×１/３＝①
正四面体の体積は、⑥－①×４＝②
よって、（３√２）³×②/⑥＝18√２ｃｍ²
＠余談終わり＠

全体の体積が18√２ｃｍ³として体積比を求める。
立体Ｐ―ＡＭＱで捉える。
底面積の比は、全体：求める立体＝△ＡＣＤ：△ＡＭＱ
隣辺比で、（３×４）/（６×６）＝１/３倍
高さの比は、全体：求める立体＝ＢＣ：ＰＣ→４/６＝２/３倍
したがって、求積すべき立体の体積は、18√２×１/３×２/３＝４√２ｃｍ³
こ…４、さ…２

＠2023年度・都立解説＠
数学(分割後期)　社会…平均55.6点　理科…平均59.4点　英語…平均62.8点
公立高校入試解説ページに戻る