2020年度　久留米大学附設高校過去問【数学】大問１解説

問題ＰＤＦ
（１）
次の連立方程式を解け。
（ｘ＋３ｙ）：（４ｘ－２ｙ）＝３：５
３ｘ－５ｙ＝12

（２）
ａ＝√３＋√15、ｂ＝√３－√15のとき、の値を求めよ。

（３）

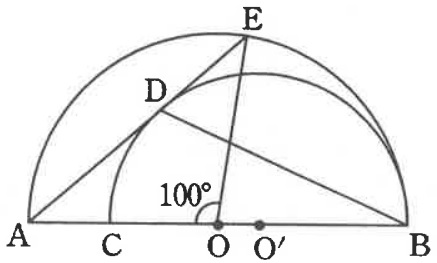
図のように、線分ＡＢ、ＣＢを直径とする大小２つの半円があり、
小さい方の半円に点Ａから接線を引き、２つの半円との接点と交点をそれぞれＤ、Ｅとする。
２つの半円のそれぞれの中心をＯ、Ｏ’とする。
∠ＡＯＥ＝100°であるとき、∠ＢＤＥの大きさを求めよ。

（４）
ｐ＋ｑ＝20、ｐ＞ｑ＞０を満たす異なる２つの正の整数ｐ、ｑの組は９組ある。
この９組のうち、√ｐ＋√ｑの値が大きいほうから３番目となる組を求めよ。

（５）
４ｍ³＋ｎ²＝2020を満たす正の整数ｍ、ｎは２組ある。その２組を求めよ。

①内項と外項の積より、
３（４ｘ－２ｙ）＝５（ｘ＋３ｙ）
12ｘ－６ｙ＝５ｘ＋15ｙ
７ｘ＝21ｙ
ｘ＝３ｙ　…③

②に代入。
３×３ｙ－５ｙ＝12
４ｙ＝12
ｙ＝３
③に代入。ｘ＝３×３＝９
ｘ＝９、ｙ＝３

（２）
対称式。
ａ＋ｂ＝（√３＋√15）＋（√３－√15）＝２√３
ａｂ＝（√３＋√15）（√３－√15）＝３²－15²＝－12
和（ａ＋ｂ）と積（ａｂ）の形に持っていく。

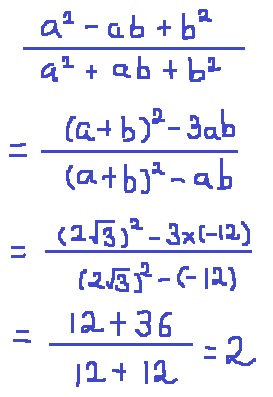
*ａ²－ａｂ＋ｂ²＝ａ²＋２ａｂ＋ｂ²－３ａｂ＝（ａ＋ｂ）²－３ａｂ

（３）

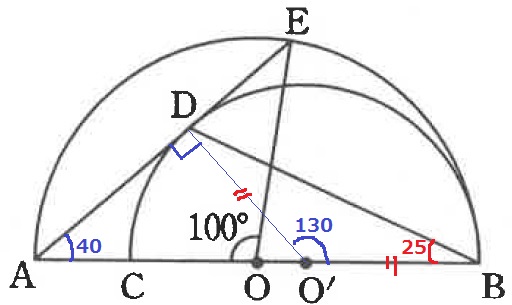
△ＡＥＯは半径より二等辺→∠ＥＡＯ＝（180－100）÷２＝40°
Ｏ’Ｄに補助線。
半径と接線は直交するので、∠ＡＤＯ’＝90°
△ＡＤＯ’の外角定理から、∠ＤＯ’Ｂ＝40＋90＝130°
△Ｏ’ＤＢも半径より二等辺→∠ＤＢＯ’＝（180－130）÷２＝25°
△ＡＤＢで外角定理→∠ＢＤＥ＝40＋25＝65°

（４）
（ｐ、ｑ）＝（19、１）（18、２）（17、３）…（11、９）の９通り。

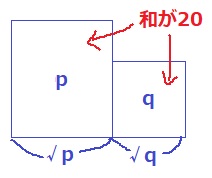
１辺が√ｐと√ｑの正方形があり、２つの面積の合計は20で一定。
このとき、√ｐ＋√ｑの長さがMaxになるのはどういうときだろう？

極端なケースを想定する。
条件はｑ＞０だが、仮にｑ＝０にしてｐの面積を20とすると、√ｐ＝√20
ｐ＞ｑを無視して、ｐ＝ｑ＝10では、√ｐ＋√ｑ＝√10＋√10＝２√10＝√40
√20＜√40だから、ｐとｑの面積が等しい場合に近いほど長さの和が大きくなるはず。
√ｐ＋√ｑの値が最も大きいのは√11＋√９、２番目は√12＋√８、３番目は√13＋√７。
（ｐ、ｑ）＝（13、７）

（５）
難しい(´ﾟωﾟ`;)
４ｍ³＋ｎ²＝2020
ｎ²＝2020－４ｍ³
ｎ²＝４（505－ｍ³）
左辺のｎ²が平方数。
４も平方数なので、505－ｍ³も平方数になるはず。
３乗が曲者だが…８×８×８＝512なのでｍは７以下。
ｍ＝１⇒505－１＝504×
ｍ＝２⇒505－８＝497×
ｍ＝３⇒505－27＝478×
ｍ＝４⇒505－64＝441＝21×21〇
ｍ＝５⇒505－125＝380×
ｍ＝６⇒505－216＝289＝17×17〇
ｍ＝７⇒505－343＝162×
*20までの平方数は暗記しておくのがベター。
ｍ、ｎは２組しかないとあるので、もう１個がでれば終了。

ｎの値は素因数に注目。（４＝２×２の２だけを抜き出す）
ｍ＝４のとき、ｎ＝２×21＝42
ｍ＝６のとき、ｎ＝２×17＝34
（ｍ、ｎ）＝（４、42）（６、34）
国私立高校入試解説ページに戻る