2020年度　久留米大学附設高校過去問【数学】大問２解説

問題ＰＤＦ

ａを正の定数とする。
放物線Ｃ：ｙ＝ａｘ²と反比例のグラフＤ：ｙ＝ａ/ｘ（ｘ＞０）の交点をＡとする。
上図のようにＣ上でＡより左側に点Ｐ、右側に点Ｑをとり、直線ＰＱとＤの交点をＲとする。
点Ｐ、Ｑのｘ座標をｐ、ｑとする。直線ＰＱの傾きがＣ、Ｄの比例定数ａと等しく、
Ｒが線分ＰＱの中点となるとき、次の問いに答えよ。
（１）
点Ａの座標をａを用いて表せ。

（２）
ｐ＋ｑの値を求めよ。

（３）
点Ｒの座標をａを用いて表せ。

（４）
ｐ、ｑの値をそれぞれ求めよ。

（５）
ＡＰ＝ＡＱとなるとき、ａの値を求めよ。

（２）
直線ＰＱの式をｙ＝ａｘ＋ｂとする。
ＰとＱはｙ＝ａｘ²とｙ＝ａｘ＋ｂの交点。
ａｘ²＝ａｘ＋ｂ
ａｘ²－ａｘ－ｂ＝０
解の公式を適用する。

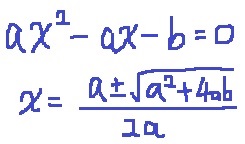
 求めたいのはｐ＋ｑの値。ｐは負、ｑは正だから…

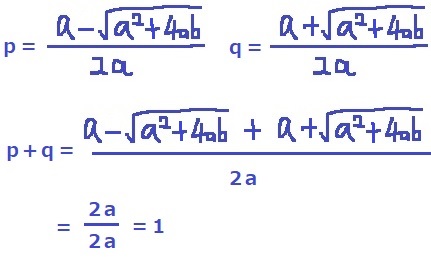
（３）
ＲはＰとＱの中点で、ＰとＱのｘ座標の和（ｐ＋ｑ）が１だから、
Ｒのｘ座標は、（ｐ＋ｑ）÷２＝１/２

これをｙ＝ａ/ｘに代入。
Ｒのｙ座標は、ｙ＝ａ÷１/２＝２ａ
Ｒ（１/２、２ａ）

（４）

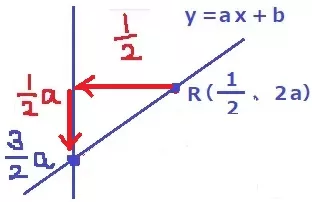
まず、直線ＰＱの切片ｂがわかる。
ｙ＝ａｘ＋ｂの傾きａは右に１いくと上にａあがる。
Ｒから切片に移動すると、左に１/２、下に１/２ａ。
ここから切片ｂは、２ａ－１/２ａ＝３/２ａ

ＰとＱはｙ＝ａｘ²とｙ＝ａｘ＋３/２ａの交点だから、
ａｘ²＝ａｘ＋３/２ａ　←÷ａ（ａ≠０）後に整理
２ｘ²－２ｘ－３＝０
解の公式を適用、ｂ＝２ｂ’が使える。
ｘ＝（１±√７）/２
ｐ＜０、ｑ＞０だから、ｐ＝（１－√７）/２、ｑ＝（１＋√７）/２

（５）

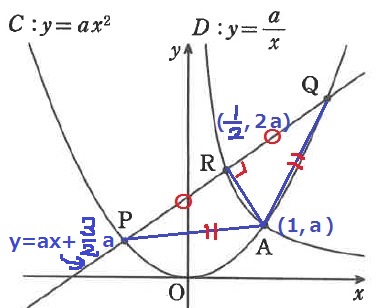
ＡＰ＝ＡＱなので、△ＡＰＱは二等辺三角形。
頂角Ａから底辺ＰＱの中点にあるＲを結ぶとＡＲ⊥ＰＱ
ＡＲの傾きは、（ａ－２ａ）/（１－１/２）＝－２ａ
２本の直線が直交するとき、傾きの積は－１。
ＰＱの傾きは、－１÷－２ａ＝１/（２ａ）　←ａは分母にある
これがｙ＝ａｘ＋３/２ａの傾きａと同じ。
ａ＝１/（２ａ）　←両辺を２ａ倍
２ａ²＝１
ａ²＝１/２
ａ＞０より、ａ＝√２/２
国私立高校入試解説ページに戻る