問題ＰＤＦ
下の図の正三角形ＡＢＣにおいて、△ＢＤＥ≡△ＧＤＥ、ＡＧ＝ＣＦ＝１、ＡＤ＝２となるように、
辺ＡＢ、ＢＣ上にそれぞれ点Ｄ、Ｅを、辺ＣＡ上に２点Ｆ、Ｇをとります。
（１）
∠ＤＥＧの大きさを求めなさい。
（２）
ＦＧの長さを求めなさい。
（３）
３点Ｅ、Ｆ、Ｇを通る円の半径を求めなさい。
＠解説＠
（１）
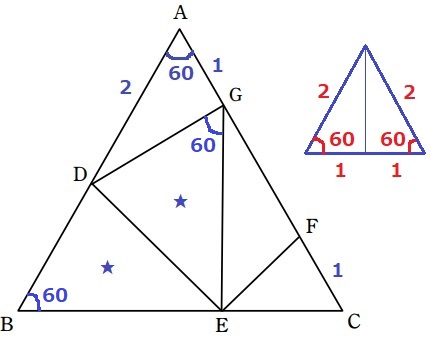
情報の多い△ＡＤＧに着目する。
辺の比が２：１で、あいだの角が60°
→同じものを２つくっつけると正三角形になる。
△ＡＤＧは１：２：√３の直角三角形→∠ＡＧＤ＝90°
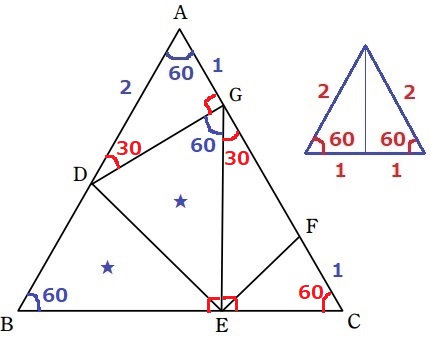
∠ＣＧＥ＝180－90－60＝30°
△ＧＣＥで外角定理→∠ＧＥＢ＝30＋60＝90°
合同より、∠ＤＥＧ＝∠ＤＥＢだから、∠ＤＥＧ＝90÷２＝45°
（２）
△ＡＤＧは１：２：√３の直角三角形→ＤＧ＝√３
合同で、ＤＢ＝√３
正三角形ＡＢＣの１辺ＡＢが２＋√３だから、
ＦＧ＝２＋√３－１－１＝√３
（３）
３点を通る円の半径を求めたい。まずは円の直径を探す。
半円の弧に対する円周角は90°だから、どこかに直角があるはずだが、
△ＥＦＧの内角を調べると∠ＥＦＧ＝90°が導けない…。
直径はＥＧではなく、別の直角を探す。
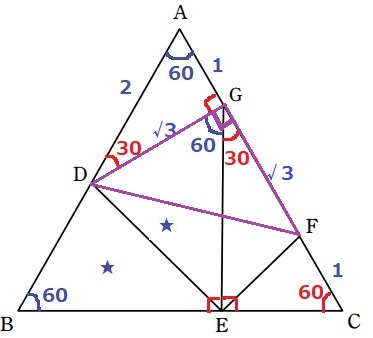
前問の解答が誘導になっている。
ＤＧ＝√３、ＧＦ＝√３、∠ＤＧＦ＝90°より、△ＤＧＦは直角二等辺三角形。
∠ＤＧＦを使いたい…。残るＥはどうか？
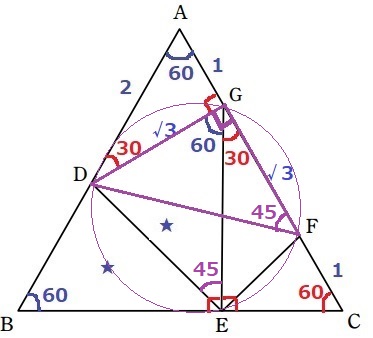
直角二等辺だから、∠ＤＦＧ＝45°
（１）より、∠ＤＥＧ＝45°!
点Ｅ、Ｆが直線ＤＧにおいて同じ側にあり、∠ＤＥＧ＝∠ＤＦＧが成り立つ。
円周角定理の逆から、４点Ｄ、Ｅ、Ｆ、Ｇは同一円周上にある！
この円の半径を求めればいい。
直径ＤＦは１：１：√２より、√３×√２＝√６
半径は√６÷２＝√６/２
国私立高校入試解説ページに戻る
コメント