問題ＰＤＦ
半径３ｃｍの球の体積は、底面が半径３ｃｍの円で、高さが６ｃｍの円柱の体積の３分の２に等しいことが知られています。このことを利用して、次の問いに答えなさい。
（１）
半径３ｃｍの球の体積を求めなさい。
（２）
図１のような直方体の箱があります。この箱の内部を半径３ｃｍの球が自由に動き回るとき、動き回ることのできる部分は図２のような立体になります。この立体の体積は、半径３ｃｍの球の体積の何倍ですか。
（３）
１辺の長さが15ｃｍの立方体の箱があります。この箱の内部を半径３ｃｍの球が自由に動き回るとき、動き回ることのできる部分の体積を求めなさい。
＠解説＠
（１）
問題文の情報から式を立てる。
３×３×3.14×６×２/３＝113.04ｃｍ3
*半径をｒ、円周率をπとして、〔球の体積Ｖ＝４/３πｒ3〕と中学１年生で習います。
（２）
おそらく、こうやって欲しいのだと思う。
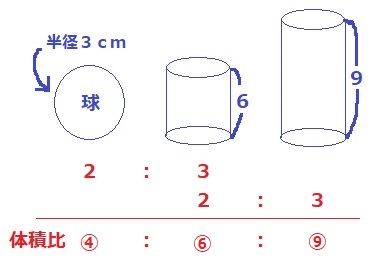
問題文から半径３ｃｍの球と、底面が半径３ｃｍ高さ６ｃｍの円柱の体積比が２：３
半径３ｃｍ高さ６ｃｍの円柱と、同じ底面で高さ９ｃｍの体積比も２：３
これを連比処理すると④：⑥：⑨
図２の立体は、球＋高さ９ｃｍの円柱だから④＋⑨＝⑬
球の体積の13/４倍。
（３）
求積すべき立体がイメージできないと太刀打ちできない。
わかりやすい場所からいきます。
15ｃｍの立方体の各頂点に８つの球を設置。
この球の中心を頂点とする立方体（１辺９ｃｍ）の内部は、球がすべて通過できる。
つづいて、内部の立方体の各６面に接する、外側の立体を考える。
１辺15ｃｍ立方体を上からみると、４つの円の中心を頂点とする１辺９ｃｍ正方形の内部は、
すべて球が通過する。立体で捉えれば、９ｃｍ×９ｃｍ×３ｃｍの直方体でこれが６つ。
*うえの図では上面と左面しか記載していません！(;^ω^)
さらに、先ほどの９×９×３の直方体の外側に注意を向けると、
半径３ｃｍ中心角90°の扇形の柱体がある。
この柱体は１辺15ｃｍの立方体の辺に１本ずつあるので合計12本。
４本集めると半径３ｃｍ高さ９ｃｍの円柱となるから、前問の体積比でいえば⑨となる。
円柱は12÷４＝３個できるので体積比の合計は㉗。
最後に立方体の８つの頂点には、それぞれ球の８分の１がある。
８つ集めると半径３ｃｍの球となり、前問の体積比でいえば④。
まとめると･･･
９×９×９＋９×９×３×６＋113.04×（㉗＋④）/④
＝729＋1458＋876.06＝3063.06ｃｍ3
＠別解＠
立方体から通過できない部分をひいてもよい。
立方体全体…15×15×15＝3375ｃｍ3
８つの角の和は、１辺６ｃｍの立方体から半径３ｃｍの球の体積をひく。
６×６×６－113.04＝102.96ｃｍ3
各辺の端は、底面積が１辺６ｃｍの正方形から半径３ｃｍの円をひいたもので、
高さが９ｃｍの空洞柱体が合計３本。
（６×６－３×３×3.14）×９×３＝7.74×27＝208.98ｃｍ3
3375－102.96－208.98＝3063.06ｃｍ3
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント