問題PDF
2つの店A、Bへ順に行き、それぞれの店で2種類の商品X、Yをいくつか買った。
①商品Xについて、店Aでは定価から10%引き、店Bでは定価から5%引きされていた。
②商品Yについて、店Aでは定価で売られていたが、店Bでは1つあたり50円引きされていた。
③店Aでは9600円、店Bでは8600円を支払ったが、
合計は商品をすべて定価で買った場合より1600円少なかった。
④2つの店で買ったものをすべて数えると、商品Xは20個、商品Yは28個あった。
⑤商品Xと商品Yの1個ずつの定価の合計は850円である。
消費税は考えないものとし、支払った金額は四捨五入などされていないものとして次の問いに答えよ。
(1)
商品Xの定価を求めよ。
(2)
店Aで買った商品Xと商品Yの個数を求めよ。
@解説@
(1)
情報が複雑で混乱しやすい。
まずはそれぞれの定価ではなく、全体を捉えよう。
商品Xの定価をx円、商品Yの定価をy円とする。
⑤より、x+y=850…【1】
③④より、商品X20個と商品Y28個の合計金額(定価)は、9600+8600+1600=19800
20x+28y=19800…【2】
【2】-【1】×20
20x+28y=19800
-)20x+20y=17000
8y=2800
y=350
【1】より、x=850-350=500
商品Xの定価は500円。
(2)
こちらも連立方程式。
1つは前問で各々の定価がわかったので支払代金から立式できる。
もう1つは値引きの側面から立式する。
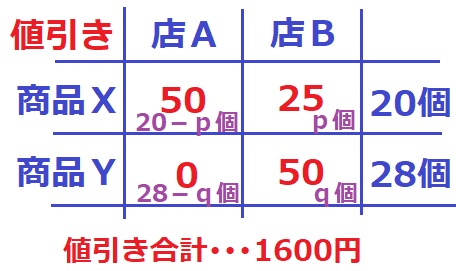
定価500円の商品Xについて、Aは10%引き→50円引き、Bは5%引き→25円引き
定価350円の商品Yについて、Aは値引きなし、Bは50円引き。
ここで店AではYの値引きが0円であることに注目して、
店Bで買ったXの個数をp、Yの個数をqとおく。
→店Aで買ったXは20-p個。Yは28-q個だが0円なので計算不要。
50(20-p)+25p+50q=1600
-25p+50q=600…①
店Bでの支払代金は8600円なので、
475p+300q=8600…②
②-①×6
475p+300q=8600
-)-150p+300q=3600
625p =5000
p=8
①に代入。
-25×8+50q=600
50q=800
p=16
B店でXは8個、Yは16個購入。
したがって、A店では、
X…20-8=12個
Y…28-16=12個
商品X12個、商品Y12個



コメント