問題PDF
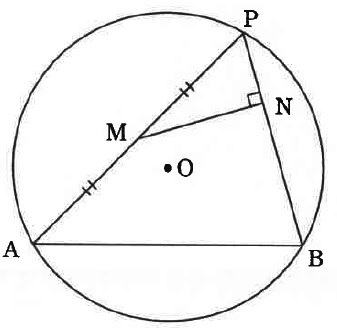
直径5の円Oの円周上にAB=4となるように2点A、Bをとる。
弧ABのうち長い方の円弧上に動点Pをとり、線分APの中点をMとし、
Mから線分PBに垂線MNを引く。次の問いに答えよ。
(1)
PAが円Oの直径となるとき、MNの長さを求めよ。
(2)
PBが円Oの直径となるとき、三角形PMNの面積を求めよ。
(3)
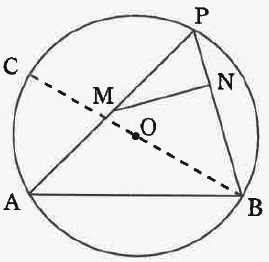
点CをBCが円Oの直径となる点と定める。
「点Pが点Aを含まない円弧BC上にあるとき、直線MNは点Pの位置に関わらず定点Qを通る。
ただし、点Pは点Bとは異なる点とする」
解答欄の図に定点Qを図示した上で、このことを証明せよ。
@解説@
(1)
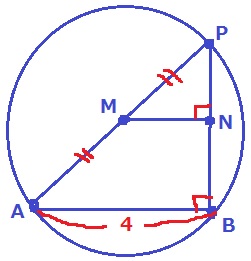
↑PAが直径のとき。Mは中心Oと重なる。
半円の弧に対する円周角は直角なので、∠ABP=90°
△PMN∽△PABより、MN=4÷2=2
(2)
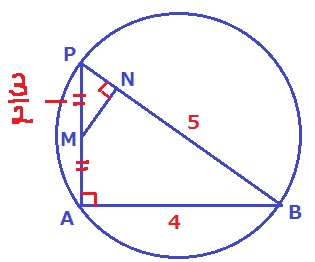
半円の弧に対する円周角で∠PAB=90°
△PBAは3:4:5の直角三角形。
面積は3×4÷2=6
MP=3÷2=3/2
面積比は相似比の2乗。
△PBA:△PMN
=52:(3/2)2
=25:9/4
=100:9
△PMNの面積は、6×9/100=27/50
(3)
難しい。
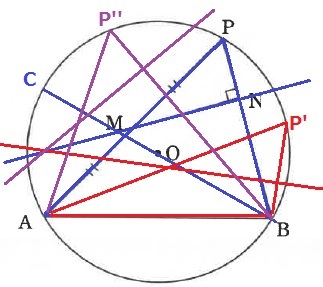
適当に調べてみると左のところに集まっている・・。
AとCのあいだっぽい。
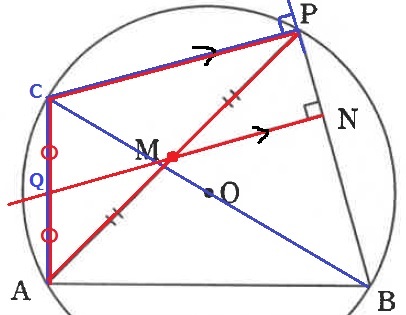
BCは直径。これに対する円周角である∠BPC=90°
同位角が等しく、CP//MN
MNとACの交点をQとする。
CP//MNから2角が等しく、△ACP∽△AQM
AQ:QC=AM:MP=1:1
定点QはACの中点にある。


(1)(2)の図から直線MNを描いてQの位置を探るのが良かったかな?



コメント