問題ＰＤＦ
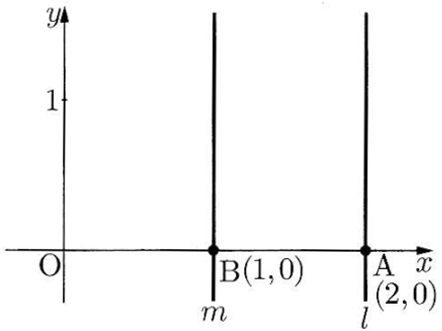
上の図のように、点Ｏ（０、０）点Ａ（２、０）点Ｂ（１、０）がある。また、直線ｌと直線ｍがあり、直線ｌの式はｘ＝２、直線ｍの式はｘ＝１である。点Ｏから点（１、０）までの距離、および点Ｏから点（０、１）までの距離をそれぞれ１ｃｍとする。
点Ｐは点Ｏを出発し、ｘ軸上をｘ座標が増加する方向に毎秒１ｃｍの速さで動く。点Ｑは、点Ｐが出発するのと同時に点Ａを出発し、直線ｌ上をｙ座標が増加する方向に毎秒１ｃｍの速さで動く。点Ｒは、点Ｐが出発してから３/10秒後に点Ｂを出発し、直線ｍ上をｙ座標が増加する方向に毎秒１ｃｍの速さで動く。
点Ｐが点Ｏを出発してからｔ秒後について、次の各問いに答えなさい。ただし、３/10＜ｔ＜１とする。
（１）
ｔ＝１/２のときの直線ＱＲの傾きを求めなさい。
（２）
３点Ｐ，Ｑ，Ｒが１つの直線上にあるときのｔの値を求めなさい。
（３）
△ＰＱＲの面積が１/10ｃｍ2になるときのｔの値をすべて求めなさい。
＠解説＠
（１）
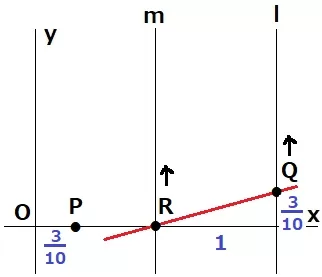
Ｒが出発するｔ＝３/10のとき、ＱＲの傾きは３/10。
これ以降はＱＲが上に平行移動するので傾きは常に３/10である。
ｔ＝１/２は３/10秒より後だから、ＱＲの傾きは３/10。
（２）
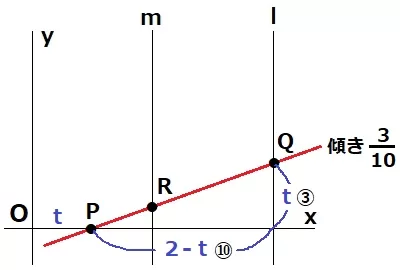
３点が一直線となるのは、ＱＲ上にＰが乗っかればいい。
両端のＰとＱだけをみる。
Ｐ→Ｑは右に２－ｔ、上にｔ。
この傾きは３/10だから、２－ｔ：ｔ＝10：３
内項と外項の積で、10ｔ＝３（２－ｔ）
ｔ＝６/13
（３）
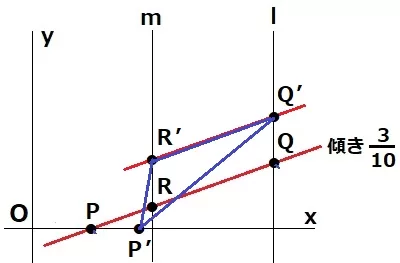
先ほどの一直線（ｔ＝６/13）のときは△ＰＱＲ＝０ｃｍ2
ここから３点を動かすと上図のようになる。
ＱＲの長さは変わらないことに目を向ける。
ＱＲを底辺とすると高さだけが長くなるので、△ＰＱＲの面積は一次関数で増加する。
一直線となるｔ＝６/13の前後で１/10ｃｍ2になるタイミングを探す。
△ＰＱＲの面積の変化の割合を求めたい。
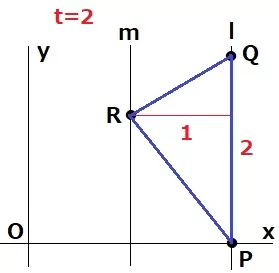
求めやすい場所はｔ＝２
（問題文では３/10＜ｔ＜１だが、ｔ≧１でも面積の変化の割合は同じ）
△ＰＱＲ＝２×１÷２＝１ｃｍ2
６/13秒のとき→０ｃｍ2
２秒のとき→１ｃｍ2
２－６/13＝20/13秒で１ｃｍ2の変化。
１/10ｃｍ2になるのは、20/13×１/10＝２/13秒
つまり、６/13秒から±２/13秒の経過で△ＰＱＲ＝１/10ｃｍ2になる。
ｔ＝６/13±２/13＝４/13、８/13
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント