問題ＰＤＦ
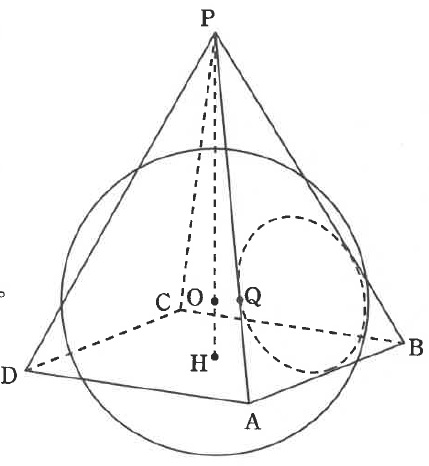
下図のような正四面体Ｐ－ＡＢＣＤがあり、すべての辺は球面Ｓに接している。
球面Ｓの中心Ｏは、頂点Ｐから底面ＡＢＣＤに引いた垂線ＰＨ上にある。
辺ＰＡと球面Ｓの接点をＱとする。
球面Ｓの半径が１、ＯＨの長さが√２/４のとき、次の問いに答えよ。
（１）
線分ＡＨの長さを求めよ。
（２）
線分ＯＡ、ＱＡの長さをそれぞれ求めよ。
（３）
線分ＰＯ、ＰＱの長さをそれぞれｘ、ｙとする。ｘ、ｙの値を求めよ。
（４）
二等辺三角形ＰＡＢの内接円の半径ｒを求めよ。
＠解説＠
（１）
問題文に数字が２つしかない。
球の半径が１なので、球と正四角錘が接するポイントを探す。
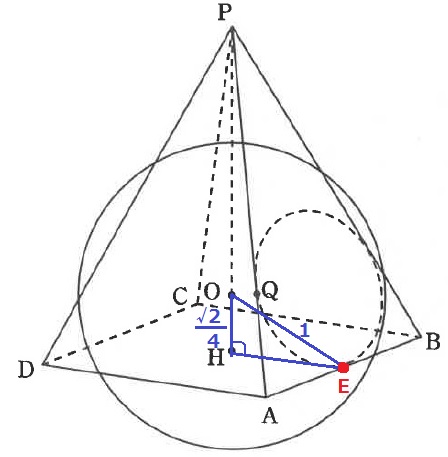
ＡＢの中点をＥとする。Ｅが接点！
△ＯＨＥで三平方。
ＨＥ2＝１2－（√２/４）2
＝１－１/８＝７/８
ＨＥ＞０より、ＨＥ＝√14/４
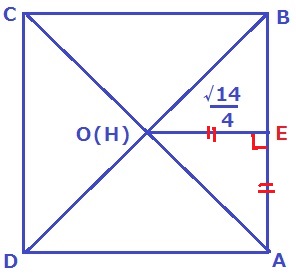
↑上からみた図。
△ＨＥＡは直角二等辺だから、ＡＨ＝√14/４×√２＝√７/２
（２）
ＯＨ＝√２/４、ＡＨ＝√７/２
△ＯＡＨで三平方。
ＯＡ2＝（√２/４）2＋（√７/２）2＝15/８
ＯＡ＞０より、ＯＡ＝√30/４
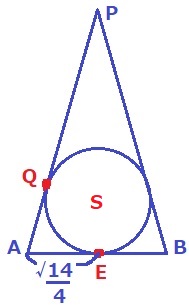
前問のＥを使う。
球面ＳとＰＡの接点がＱ。
Ｅも球面上にあるＡＢとの接点。
△ＡＰＢで球面ＳはＡＰ上でＱと、ＡＢ上でＥと接する。
そして、円外の点から接点までの接線の長さは等しい。
ＱＡ＝ＥＡ＝√14/４
（３）
（２）と同じで２本の線分の長さを求めるが、
わざわざｘ、ｙに置き換えているということは連立を組めということ。
ＰＯとＰＱを１辺とする三角形で相似関係を見つける。
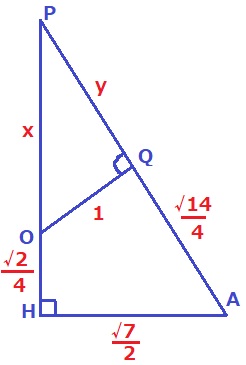
ズバリ、△ＰＡＨ∽△ＰＯＱ
ＰＯ：ＯＱ＝ＰＡ：ＡＨから、
√７/２ｘ＝ｙ＋√14/４ …①
ＰＱ：ＱＯ＝ＰＨ：ＨＡから、
√７/２ｙ＝ｘ＋√２/４ …②
これを解けばいいが、計算処理が辛い…。
以下、代入法です。
ｘ＝３√２/２、ｙ＝√14/２
（４）
ＰＡ＝ＰＱ＋ＱＡ＝√14/２＋√14/４＝３√14/４
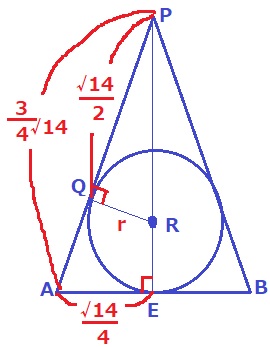
球面Ｓの中心をＲとする。
△ＡＰＥで三平方→ＰＥ＝√７
△ＡＰＥ∽△ＲＰＱよりＱＲの長さは、
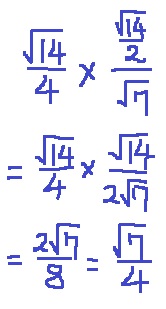
ｒ＝√７/４
国私立高校入試解説ページに戻る
コメント