2020年度　慶應義塾高校過去問【数学】大問１解説

問題ＰＤＦ
次の空欄をうめよ。
（１）
√24の小数部分をａとするとき、
ａ²+８ａ＝〔　　　　〕である。

（２）
を既約分数に直すと、〔　　　　〕である。

（３）
３ｘ²－15ｘ＋７＝０のとき、３ｘ⁴－15ｘ³＋35ｘ－16の値は〔　　　〕である。

（４）
50人の生徒がＡ、Ｂ２つの問いに答えたところ、Ａを正解した生徒が32人、Ｂを正解した生徒が28人だった。このとき、Ａ、Ｂともに不正解となった生徒の人数は最大で〔　　　〕人、また、Ａ、Ｂともに正解した生徒の人数は最小で〔　　　〕人である。

（５）
長さも太さも色も同じひもが３本ある。ひもをすべて半分に折り、折った箇所を袋の中に隠し、ひもの両端が袋から出た状態のくじを作った。Ａ，Ｂ、Ｃ、Ｄ４人の生徒が順に６本のひもの端から１つずつ選んだとき、同じひもの両端を選ぶペアが２組となる確率は〔　　　〕である。

（６）
箱の中に入ったビー玉のうち、125個を取り出して印をつけ、元に戻した。よくかきまぜてｘ個取り出して調べたところ、印のついたビー玉が35個含まれていたため、箱に入ったビー玉は全部で１万個と推定した。ｘ＝〔　　　〕である。

（２）

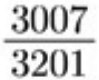
↑これを約分しなさいという直球(*’ω’*)w
小学生でも解けるが、ここでモタモタすると焦って大問７まで手が届かないよΨ(｀∀´)Ψ
差に注目すると、3201－3007＝194
3201と3007で約分できるということは、差の194の約数の何かで約分できる。
194の約数は〔１・２・97・194〕_{意外と少ない！}
２と194は偶数なので、奇数の3201と3007と相性が悪い×
そこで97に絞って計算してみる。
3007÷97＝31
3201÷97＝33
（3201－3007＝194＝97×２→31＋２＝33）
よって、31/33。

（３）
３ｘ²－15ｘ＋７＝０のとき→３ｘ⁴－15ｘ³＋35ｘ－16
式を比較すると、【３ｘ²－15ｘ】と【３ｘ⁴－15ｘ³】の部分が似ている…。
３ｘ²－15ｘ＝－７と変形。
３ｘ⁴－15ｘ³＋35ｘ－16
＝ｘ²（３ｘ²－15ｘ）＋35ｘ－16
＝－７ｘ²＋35ｘ－16

さらに３ｘ²－15ｘの形が作れないか模索する。
－７ｘ²＋35ｘ－16
＝－７（ｘ²－５ｘ）－16
＝－７÷３×３×（ｘ²－５）－16　←÷3×3で値は変わらない。（－７÷３）×｛３×（ｘ²－５）｝ｰ16
＝－７/３（３ｘ²－15）－16
＝－７/３×（－７）－16＝１/３

（４）
ベン図を利用。

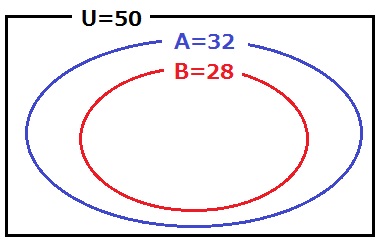
２問とも不正解した者を最も多くする。
数の少ないＢの正解者は全員Ａも正解した。
ＢがＡに包含すると、Ａの外側にいる２問不正解者の領域が最も広くなる。
50－32＝28人

今度は２問とも正解した者を最も少なくする。
２問不正解者をゼロにして、50人全員が少なくとも１問は正解したと想定する。
Ａの集合を左に、Ｂの集合を右に寄せると、ＡとＢが重なった領域が最も狭くなる。
（32＋28）－50＝10人
【解答】28人・10人

（５）

ヒモは３本、ヒモの端は６本。
組み合わせが良いかな？
４人が６本の端を選ぶ組み合わせは、₆Ｃ₄＝₆Ｃ₂＝15通り

２組のペアをつくる。
３本のヒモのうち、ペアが成立する２本のヒモを選ぶ。
→選び方は３通り。
３/15＝１/５
*発想が求められるので難しい。。
ちなみに、ひも４本で同様に計算すると、
端８本から４人がそれぞれ１本を選ぶ→₈Ｃ₄＝70通り
４本のヒモからペアができる２本を選ぶ→₄Ｃ₂＝６通り
確率は６/70＝３/35となる。

（６）
標本の大きさを求める。
印付きのビー玉は【ｘ個中35個】。
印付きは全体で125個で、ビー玉全部を10000個と推定したということは、
印付き：全体＝35：ｘ＝125：10000
ｘ＝10000×35/125＝2800
国私立高校入試解説ページに戻る