問題ＰＤＦ
Ａ、Ｂ２人がＰ地を出発してＱ地へ向かい、Ｑ地に到着するとすぐＰ地へ引き返す。
ＡはＢより15分遅れて出発したが、Ｑ地より２ｋｍ手前の地点で追いつき、
その９分後にＱ地に向かうＢと再び出会った。
その後、ＡがＰ地に到着したとき、ＢはＰ地より４ｋｍ手前の地点をＰ地に向かっていた。
Ａ、Ｂ２人の速さは毎時何ｋｍか。また、ＰＱ間は何ｋｍか。
＠解説＠
あらかじめ宣言しておきます。
算数でやるよ！
まずは情報整理。ダイヤグラムでまとめてみよう。
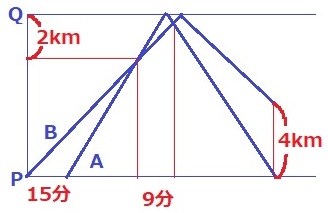
情報量が少ない(;´Д｀)
ポイントはＱの手前２ｋｍ…Ｐの手前４ｋｍ…
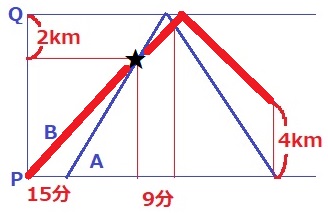
ＡがＢに追いついた★に注目しよう。
Ｂが移動した距離を考えると、Ｂの出発から★まではＰＱ－２ｋｍ。
Ｂの出発からグラフの最後まではＰＱ×２－４＝２×（ＰＱ－２）ｋｍ！
Ｂの速さは一定で距離が２倍ということは、★はＢの移動距離のちょうど真ん中にあたる。
言い換えれば、Ｂ出発～★までの時間と、★～グラフの最後までの時間が等しい。
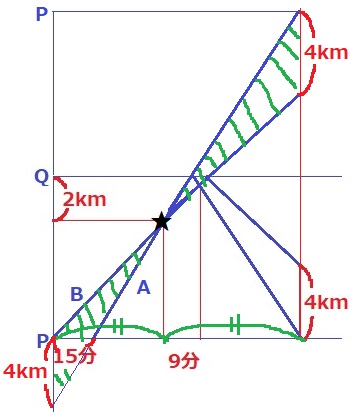
Ｑ地点を対称の軸として、うえにもう１つのダイヤグラムを線対称で追加。
時間が等しい＝横軸が同じなので、緑の斜線で示した２つの三角形が合同になる。
４ｋｍを左下に移動。
ＡはＢより15分遅れで出発したが、仮にＡとＢが同時に出発したと仮定すると、
ＡがＢの４ｋｍ後方からスタートして競走すればうえのグラフのようになる。
左下に注目。Ａは15分で４ｋｍ移動するから、速さは４×60/15＝時速16ｋｍ
つぎに、まだ使っていない９分を検証。
ＡがＢに追いついてから再び出会うまでに両者が動いた距離の合計は２ｋｍ×２＝４ｋｍ
Ａ＋Ｂの速さは９分で４ｋｍ移動→４×60/９＝時速80/３ｋｍ
Ｂの速さは、80/３－16＝時速32/３ｋｍ
仮にＡがＢの４ｋｍ後方からスタートしたとする。
両者は１時間あたり、16－32/３＝16/３ｋｍずつ差が縮まる。
４ｋｍ÷16/３＝３/４時間
→Ｂが出発してから３/４時間後に★でＡに追いつかれる。
Ｐ地から★までの距離は、32/３×３/４＝８ｋｍ
ＰＱ間の距離は８＋２＝10ｋｍ
Ａの速さ…毎時16ｋｍ、Ｂの速さ…毎時32/３ｋｍ、ＰＱの距離…10ｋｍ
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント