2020年度　ラ・サール高校過去問【数学】大問２解説

問題ＰＤＦ
（１）
座標平面上に２点Ａ（１、０）、Ｂ（０、２）があり、
直線ｙ＝１/４ｘ＋ｋとｘ軸との交点をＣとする。
直線ｙ＝１/４ｘ＋ｋが∠ＡＣＢを二等分するとき、定数ｋの値を求めよ。

（２）

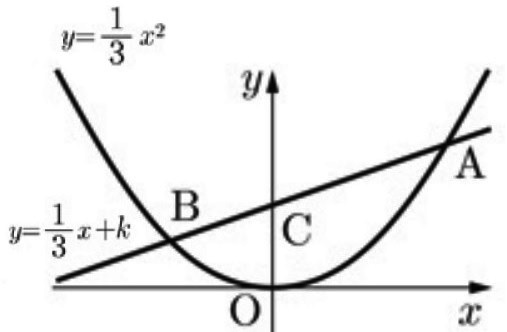
放物線ｙ＝１/３ｘ²と直線ｙ＝１/３ｘ＋ｋが上図のように２点Ａ、Ｂで交わっている。
直線ｙ＝１/３ｘ＋ｋとｙ軸との交点をＣとし、原点をＯとする。
ＡＣ：ＣＢ＝５：３のとき、定数ｋの値、および三角形ＯＡＢの面積Ｓを求めよ。

（３）
12、330、1221のように２種類の数字のみからなる正の整数について、次に答えよ。
（ア）このような整数で２けたのものはいくつあるか。
（イ）このような整数を小さい順に並べたとき、2020は何番目か。

（４）

上図のように、長方形ＡＢＣＤの各辺を直径とする半円との交点で作られる
長方形ＥＦＧＨの面積は、長方形ＡＢＣＤの面積の何倍か。
ただし、ＢＣ、ＡＤを直径とする半円は、それぞれ辺ＡＤ、ＢＣと接している。

＠解説＠
（１）

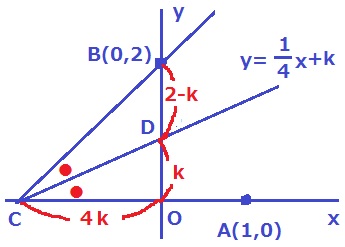
↑ｙ＝１/４ｘ＋ｋとｙ軸の交点をＤとしてグラフを描くとこうなる。
ＯＤ＝ｋ
傾き１/４→変化の割合が右に４、上に１→ＯＣ＝４ｋ。
ＤＢ＝２－ｋ

等角●をどう利用するか？→角の二等分線の定理。
〔ＣＯ：ＣＢ＝ＯＤ：ＤＢ〕
４ｋ：ＣＢ＝ｋ：２－ｋ
ＣＢ＝（２－ｋ）×４ｋ/ｋ＝－４ｋ＋８　…①

一方で、△ＢＯＣに三平方を適用。
ＣＢ²＝（４ｋ）²＋２²
ＣＢ²＝16ｋ²＋４　…②
（ＣＢの値は右辺の処理が難しいのでこのままで保留しておく）

①を２乗。
ＣＢ²＝（－４ｋ＋８）²＝16ｋ²－64ｋ＋64　…③
②と③でＣＢ²を通じて等式。
16ｋ²＋４＝16ｋ²－64ｋ＋64
64ｋ＝60
ｋ＝15/16

（２）

ＡＣ：ＣＢ＝５：３
Ａのｘ座標を５ｔ、Ｂのｘ座標を－３ｔとする。
Ａ（５ｔ、25/３ｔ²）Ｂ（－３ｔ、３ｔ²）

うえのように△ＡＢＤをつくる。
変化の割合＝ｙの増加量÷ｘの増加量
＝（25/３ｔ²－３ｔ²）÷｛５ｔ－（－３ｔ）｝
＝16/３ｔ²÷８ｔ＝２/３ｔ
これが傾き１/３に等しい。
２/３ｔ＝１/３
ｔ＝１/２

Ｂ座標に代入→Ｂ（－３/２、３/４）
これをｙ＝１/３ｘ＋ｋに代入。
３/４＝１/３×（－３/２）＋ｋ
ｋ＝５/４

△ＯＡＢは底辺が８ｔ＝４、高さ５/４だから、
Ｓ＝４×５/４÷２＝５/２
ｋ＝５/４、Ｓ＝５/２

（３）ア
２桁の整数は10～99の90個。
このうち、１種類の数字しか使わないゾロ目は11、22、33…99の９個。
90－９＝81個

イ
３桁を考える。
気をつけるべき点は最高位に０が使えないこと！
そこで０を含むか含まないかで場合分け。
■０を含む。
百の位は１～９の９通り。
百の位が１のとき、〔100・101・110〕の３通りだから、
全部で３×９＝27個
■０を含まない。
２種類の数字をＡ、Ｂとする。
Ａが２つ入る並び方は〔ＡＡＢ〕〔ＡＢＡ〕〔ＢＡＡ〕の３通り。
Ａに入る数字は１～９の９通り。Ａ、Ｂに入る数字の組み合わせは９×８＝72通り
（Ｂが２つ入る並びは、ＡとＢに入れる数字を逆にしてカウントしている）
全部で72×３＝216個
よって、３桁の数は27＋216＝243個

つづいて、千の位が１の数を考える。

１以外の他の数をＣとする。
それぞれの位は１orＣの２通り。1111は１種類だけなので除く。
２×２×２－１＝７通り
Ｃは１以外で９通りだから、全部で９×７＝63個

最後に千の位が２で2020までを数える。
千の位は２、百の位は０なので、使用すべき数は０と２で決まる。
〔2000・2002・2020〕で３個。

したがって、2020は81＋243＋63＋３＝390番目

（４）
難しい(#ﾟДﾟ)
どこの長さもわかっておらず、初手がつかみにくい。

Ｅは大きい半円と小さい半円の交点。
直径に対する円周角は直角だから、∠ＡＥＢ＝∠ＢＥＣ＝90°となり、ＡＥＣは一直線。
Ｇについても同様のことが言え、ＥとＧは長方形ＡＢＣＤの対角線ＡＣ上にある。

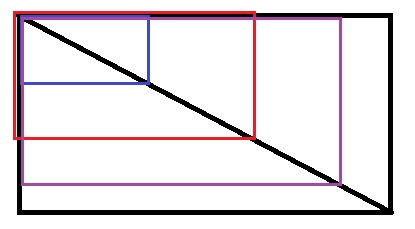
２つの長方形の対角線が同一直線上にあると、長方形の縦と横の辺は平行関係にある。
つまり、２つの長方形は∽！

●＋×＝90°で角度の調査。
△ＡＢＣ∽△ＡＥＢ∽△ＢＥＣ

相似比を確定したいが、長さがどこもわかっていない。
手がかりは２種類の半円の直径。
小さい半円の直径ＡＢ＝①とすると、大きい半円の直径ＢＣ＝②
直角三角形ＡＢＣの縦：横＝①：②となる。

直角三角形ＡＥＢにおいて、ＡＥ＝①とするとＢＥ＝②
直角三角形ＢＥＣにおいて、ＢＥ＝②からＥＣ＝④
△ＡＥＢと△ＣＧＤは対称性から合同→ＣＧ＝ＡＥ＝①
ＥＧ＝④－①＝③
長方形ＡＢＣＤと長方形ＥＦＧＨの辺の比は対角線の比ＡＣ：ＥＧ＝⑤：③
面積比は辺の比の２乗→25：９
したがって、長方形ＥＦＧＨの面積は長方形ＡＢＣＤの９/25倍。

*半円というと、円の中心点から半径を作図するのが定石ですが、
本問は直角を使わないと解けない？と思うので、
直径に対する円周角→直角三角形の相似に焦点を当てたほうが良いと思います。
国私立高校入試解説ページに戻る