問題ＰＤＦ
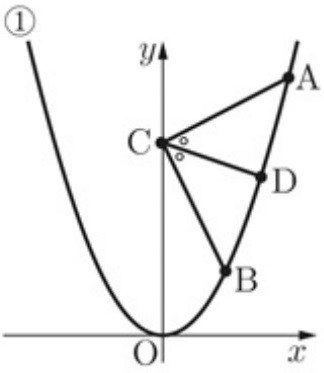
図において、①はｙ＝ａｘ2のグラフである。
２点Ａ（４、８）、Ｂ（２、ｂ）は①上の点で、点Ｃ（０、ｃ）はｙ軸上の点である。
また、∠ＡＣＢの二等分線と①の交点のうち、ｘ座標が正である点をＤとする。
このとき、次の（ ）をうめなさい。
（１）
ａ＝（ア）/（イ）、ｂ＝（ウ）である。
（２）
ｃ＝11/２のとき、△ＡＣＢの面積は（エオ）/（カ）である。
（３）
ＡＣ＋ＣＢが最小になるとき、ｃ＝（キ）であり、ＣＤ＝（ク）√（ケ）である。
＠解説＠
（１）
ｙ＝ａｘ2にＡ（４、８）を代入。
８＝16ａ
ａ＝１/２
ｙ＝１/２ｘ2にｘ＝２を代入。
ｂ＝１/２×２2＝２
ア…１、イ…２、ウ…２
（２）
ＡＢの式を求める。
Ｂ（２、２）→Ａ（４、８）
右に２、上に６移動するので、傾きは６/２＝３
Ｂ（２、２）から左に２、下に６移動して切片は－４。
ＡＢ；ｙ＝３ｘ－４
ＡＢとｙ軸の交点をＥとする。
ＣＥ＝11/２＋４＝19/２
ＡとＢのｘ座標からＢはＡＥの中点である。
ＡＢ、ＢＥを底辺とすると、△ＡＣＢと△ＢＣＥの高さは等しい。
△ＡＣＢと△ＢＣＥの面積は等しく、△ＡＣＢは△ＡＣＥの面積の半分。
19/２×４÷２÷２＝19/２
エ…１、オ…９、カ…２
（３）
ＡＣ＋ＣＢが最小→線対称。
ｙ軸についてＢを対称移動させた点をＢ’とする。
Ｂ’（－２、２）
Ｂ’Ａに注目。
Ｂ’→Ａの移動は右に６、上に６なので傾きは１。
切片はＢ’から右に２、上に２で４。
Ｃ（０、４）
ｃ＝４
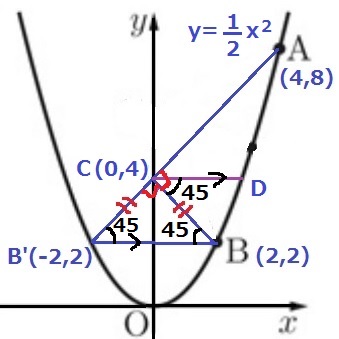
Ｂ’Ａの傾きは１で45度。
線対称からＣＢの傾きも45度で、∠Ｂ’ＣＢ＝90°
△ＢＣＢ’は直角二等辺三角形で、∠ＣＢＢ’＝45°
∠ＢＣＡ＝90°、二等分線から∠ＤＣＢ＝45°
∠ＤＣＢ＝∠ＣＢＢ’＝45°で錯角が等しく、Ｂ’Ｂ//ＣＤ。
Ｄのｙ座標はＣと同じ４。これをｙ＝１/２ｘ2に代入。
４＝１/２ｘ2
８ｘ2＝０
ｘ＞０から、ｘ＝２√２
ＣＤの長さはＤのｘ座標と等しいので２√２。
キ…４、ク…２、ケ…２
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント