2022年度　都立日比谷高校過去問【数学】大問４解説

問題ＰＤＦ
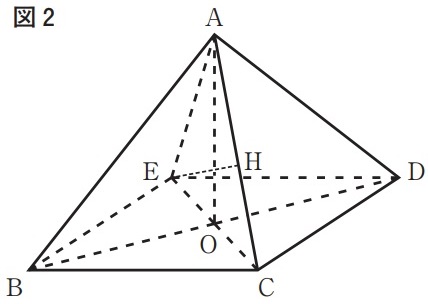
下の図１に示した立体Ａ—ＢＣＤＥは、底面ＢＣＤＥがひし形で、ＡＣ＝ＡＥ＝ＢＣ＝８ｃｍ、ＡＢ＝ＡＤの四角すいである。四角形ＢＣＤＥの対角線ＢＤ、ＣＥを引き、交点をＯとし、頂点Ａと点Ｏを結んだとき、∠ＡＯＢ＝90°である。四角形ＢＣＤＥの面積をＳｃｍ²とする。

問１
下の図２は、図１において、頂点Ｅから辺ＡＣに垂線を引き、
辺ＡＣとの交点をＨとした場合を表している。
線分ＥＨの長さは何ｃｍか。Ｓを用いた式で表せ。

問２
下の図３は、図１において、辺ＡＢ上の点をＰとし、点Ｐと頂点Ｃ、
点Ｐと頂点Ｄ、点Ｐと頂点Ｅをそれぞれ結んだ場合を表している。
（１）ＡＰ：ＰＢ＝１：２、ＢＤ＝12ｃｍのとき、立体Ｐ―ＢＣＤＥの体積は何ｃｍ³か。
ただし、答えだけでなく、答えを求める過程が分かるように、途中の式や計算なども書け。

（２）ＡＰ：ＰＢ＝１：１のとき、△ＣＥＰの面積は何ｃｍ²か。
Ｓを用いた式で表せ。

＠解説＠
問１
ここで間違えると差が開いてしまう。

底面ＢＣＤＥ＝Ｓｃｍ²と奇妙なところに文字がつけられている。
△ＡＣＥにおいて底辺をＡＣとすると高さはＥＨ。△ＡＣＥの面積が知りたい。

３辺の長さが等しく、△ＢＣＥ≡△ＡＣＥ
△ＢＣＥは菱形ＢＣＤＥの半分で１/２Ｓ。

△ＡＣＥ＝８×ＥＨ÷２＝１/２Ｓ
ＥＨ＝１/２Ｓ×２÷８＝１/８Ｓ

問２（１）

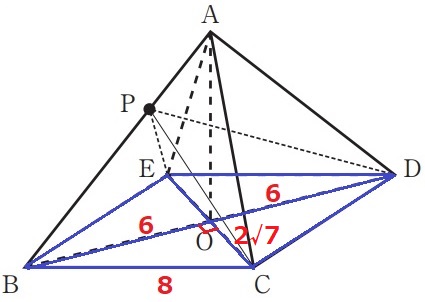
菱形の対角線は各々を垂直に２等分する。
ＢＯ＝12÷２＝６ｃｍ
△ＢＣＯで三平方→ＣＯ＝２√７ｃｍ
ＥＣ＝２√７×２＝４√７ｃｍ
菱形ＢＣＤＥの面積は、12×４√７÷２＝24√７ｃｍ²

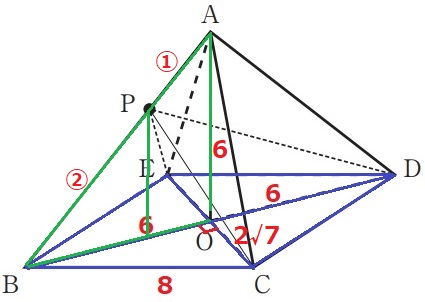
前問の合同から、ＡＯ＝ＢＯ＝６ｃｍ
四角錘Ｐ―ＢＣＤＥの高さは、６×②/③＝４ｃｍ
体積は、24√７×４÷３＝32√７ｃｍ³

（２）

斜めに傾いている△ＣＥＰの面積と底面の菱形ＢＣＤＥを結び付けたい。
△ＣＥＢ＝１/２Ｓ
△ＣＥＢと△ＣＥＰはＣＥで底辺共通なので、高さのＢＯ：ＰＯが面積比にあたる。

ＢＯとＰＯが同一平面にくる場所を探す⇒△ＡＢＯで切り取る。
本問も問１がカギになる。
△ＣＥＢ≡△ＣＥＡよりＢＯ＝ＡＯゆえ、△ＡＢＯは直角二等辺三角形。
ＰはＡＢの中点だから、△ＰＢＯも直角二等辺。
ＢＯ：ＰＯ＝√２：１
したがって、△ＣＥＰの面積は、１/２Ｓ×１/√２＝√２/４Ｓｃｍ²
国私立高校入試解説ページに戻る