平均21.8点(50点満点、前年比;-0.8点)

問題はこちら→リセマムさん
大問1(計算)
(1)① 97.4%
-1-5
=-6
② 92.9%
(-12)÷4/3
=(-12)×3/4
=-9
③ 92.4%
3(2x-y)-(x-5y)
=6x-3y-x+5y
=5x+2y
④ 91.6%
√20+√5
=2√5+√5
=3√5
(2) 81.8%(部分正答0.5%)
y=axに代入。
-15=3a
a=-5
y=-5x
大問2(小問集合)
(1) 55.9%
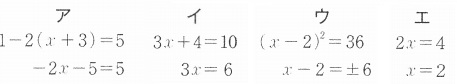
アは左辺のカッコを展開。イは両辺を-4
ウは両辺の2乗を平方根へ。エは両辺を÷2
イ
(2) 7.1%!!(部分正答0.2%)
先月の個数を【100】とすると、今月の個数は【125】
a×100/125=4/5a
(3) 42.8%
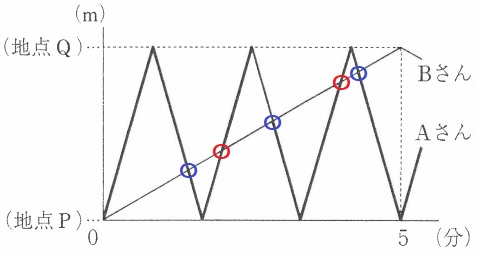
〇はAとBが出会う場所。
〇はAがBを後ろから追い越す場所。
2回
(4) 39.1%
側面の扇形の中心角は〔×半径/母線〕で処理。
8×8×π×2/8=16πcm2
(5) 24.0%!(部分正答9.8%)
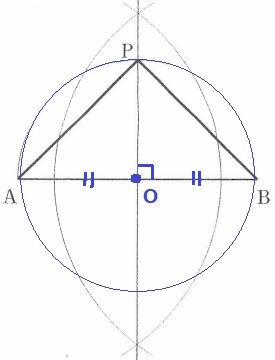
完成形をイメージしよう。
ABの垂直二等分線を対称の軸とすると、直角二等辺ABPは左右対称。
→Pは垂直二等分線上にある。
円の中心OからA・B・Pは等距離にあるので、OAを半径とする円をひく。
円周との交点がPとなる。
大問3(確率・標本調査)
(1)① 84.1%
Aで0を出す。Bは何でも良い。
Bの1~6で6通り
② 21.3%!
整数にならない場合のほうが少ないので、こちらを考える。
根号が外れて整数になる→abの積が平方数
◆ab=1
(1、1)
◆ab=4
(1、4)(4、1)(2、2)
◆ab=9
(3、3)
◆ab=16
(4、4)
◆ab=25
(5、5)
7通り
また、0は整数だから前問のab=0も整数。
計13通り
整数にならない場合は36-13=23通り
全体は6×6=36通り
確率は23/36
(2)① 90.2%
(22+17+18+23+20)÷5
=20個
② 50.4%(部分正答16.1%)
答案では、根拠となる数値を示したうえで理由を記述する。
無作為に抽出した60個のうち、赤の個数:白の個数=40:20=2:1
この割合は母集団も同じとみなす。
白は400個なので、赤は400×2/1=800個
したがって、袋の中の赤は640個以上であると考えられる。
ア
大問4(方程式)
(1) 53.6%(部分正答13.7%)
ここも求める過程を記述する。
50円硬貨の枚数をx枚、10円硬貨の枚数をy枚とする。
100円硬貨は8枚だから、50円硬貨と10円硬貨は残りの72枚。
x+y=72…①
『10円硬貨は50円硬貨の枚数の2倍より6枚多かった』
y=2x+6…②
①、②を解くとx=22、y=50
50円硬貨の枚数…22枚、10円硬貨の枚数…50枚
(2) 36.4%
ゆうとの12回目までの貯金総額は、100×8+50×22+10×50=2400円
12回で2400円だから、4000円貯まったときの貯金回数は12×4000/2400=20回
残りの貯金回数は20-12=8回
姉は8回で4000円を貯める。4000÷8=500円
大問5(平面図形)
1.0%!!!(部分正答4.8%!)
証明1題。踏むべき手順が多く、他の都道府県より難しい。
〔証明1〕
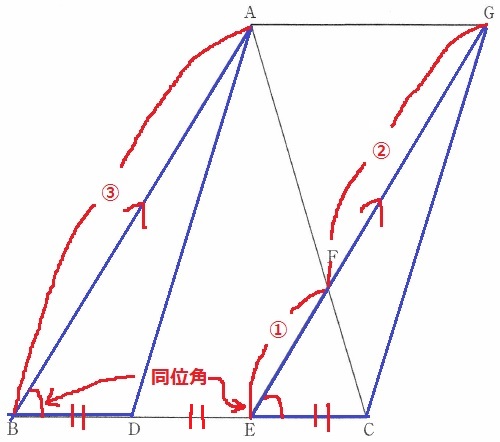
△ABDと△GECにおいて、仮定からBD=EC
AB//GE→同位角で∠ABD=∠GEC
AB//FE→2角が等しく△ABC∽△FEC→三角形と比の定理より、
AB:FE=CB:CE=③:①
仮定のEG=3EFから、GE=③
AB=GE=③(同じ比だから長さが等しい)
2辺とその間の角度が等しいので△ABD≡△GEC
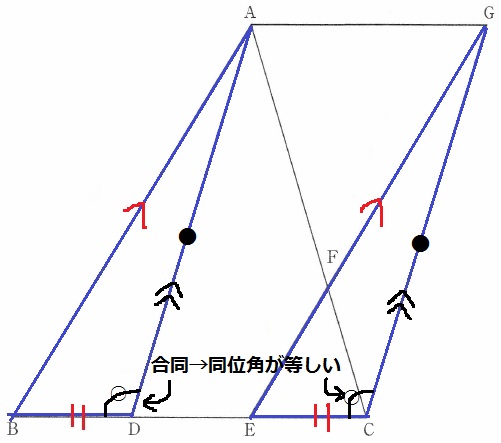
対応する辺でAD=GC
対応する角で∠BDA=∠ECG
同位角が等しく→AD//GC
1組の対辺が平行でかつ長さが等しいから、四角形ADCGは平行四辺形である。
*ADとGCに注目した証明。
三角形の合同証明に三角形と比の定理を使う点が難しい。
〔証明2〕
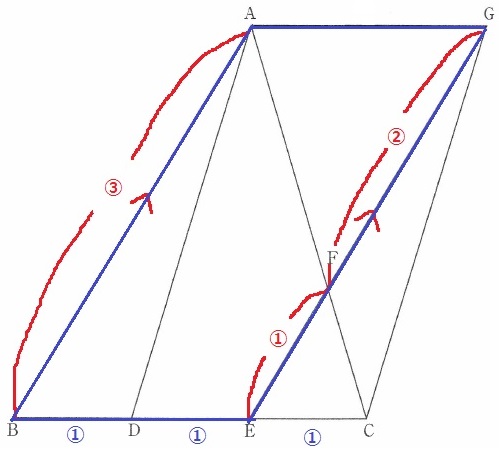
↑ここまでは先ほどと同様。
AB//GE、AB=GE
1組の対辺が平行でかつ等しい→四角形ABEGが平行四辺形。
AG//BE(AG//DE)
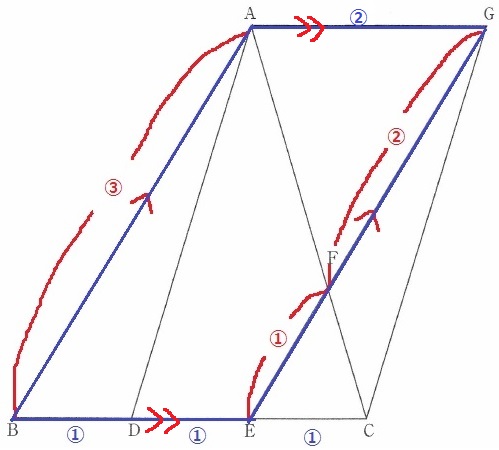
対辺が等しく、AG=BE=②
ここで平行四辺形ABEGから四角形ADCGに切り替える。
AG//DCで、AG=DC=②
1組の対辺が平行でかつ長さが等しいから、四角形ADGCは平行四辺形である。
*平行四辺形ABEGを経由した証明。サボはこちらで解きました。
大問6(関数)
(1) 68.4%
y=2x+3の式にx=-1を代入。
A(-1、1)
これをy=ax2に代入。
1=1a
a=1
(2)① 34.9%(部分正答0.6%)
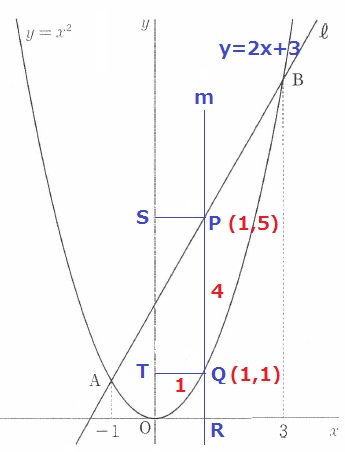
点の位置は正確に!
x座標は1だからP(1、5)Q(1、1)
長方形STQPの周の長さは(1+4)×2=10
② 4.2%!!(部分正答2.3%)

Pのx座標tで各座標を表す。
P(t、2t+3)
Q(t、t2)
長方形STQPの周の長さは、{t+(2t+3-t2)}×2=-2t2+6t+6
QRを1辺とする正方形の周の長さは、t2×4=4t2
-2t2+6t+6=4t2
6t2-6t-6=0 ←両辺を÷6
t2-6t-6=0
因数分解ができないので解の公式を適用。
t=(1±√5)/2
仮定より0<t<3だから、t=(1+√5)/2
大問7(空間図形)
(1) 65.2%
△APQは等辺を2√2cmとする直角三角形。
1:1:√2より、PQ=2√2×√2/1=4cm
(2) 13.2%!

上に三角錐を追加。延長線の交点をIとする。
三角錐I-APQと三角錘I-EFHの相似比は1:2
IA=6cm
△IPAで三平方→IP=√44cm
△IPQは二等辺で、頂角Iから底辺PQに垂線を引くと交点JはPQの中点となる。
PJ=2cm
△IPJで三平方→IJ=2√10cm
△IPQの面積は、4×2√10÷2=4√10cm2
△IPQ:△IFHの面積比は①:④だから、
四角形PFHQの面積は、4√10×③=12√10cm2
(3) 1.0%!!!
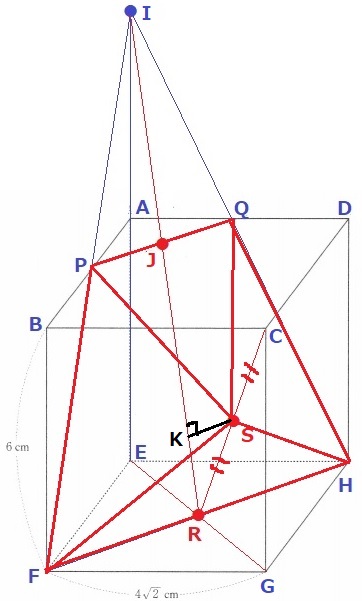
先ほど四角形PFHQの面積を出したので、これを底面とする高さが知りたい。
Sから四角形PFHQに垂線、足をKとする。
すると、KはJR上にくる。
図形全体を上からみると、IRとCRは底面の正方形の対角線EGとかぶるので、
平面AEGC上にJR、CR、KSが含まれる。
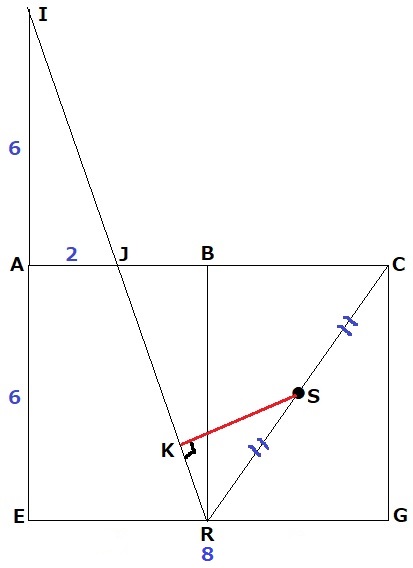
EGは直角二等辺EFGの1:1:√2より8cm。
AJは△IAJ:△IERの辺の比1:2から2cm。
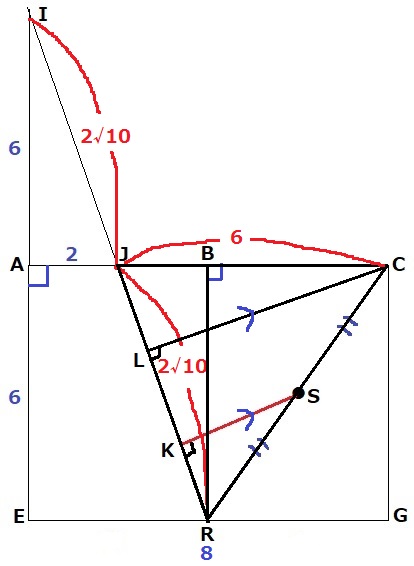
ポイントは、SがCRの中点にある情報を活用する。
Cを通るKSに平行な線を引き、IRとの交点をLとする。
△RKS∽△RLCから、KS:LC=RS:RC=2:1
LCの長さの半分がKSに値する。
ここで△CJRに着目。
この三角形の面積の出し方を2通りであらわすと…
〔底辺JC×高さBR÷2=底辺JR×高さLC÷2〕
△IAJ∽IERよりJはIRの中点だから、JR=IJ=2√10cm
JC=8-2=6cm、BR=6cmなので、
6×6÷2=2√10×CK÷2
LC=18√10/10cm
KS=LC÷2=18√10/10÷2=9√10/10
四角錐S-PFHQの体積は、12√10×9√10/10÷3=36cm3
@別解@
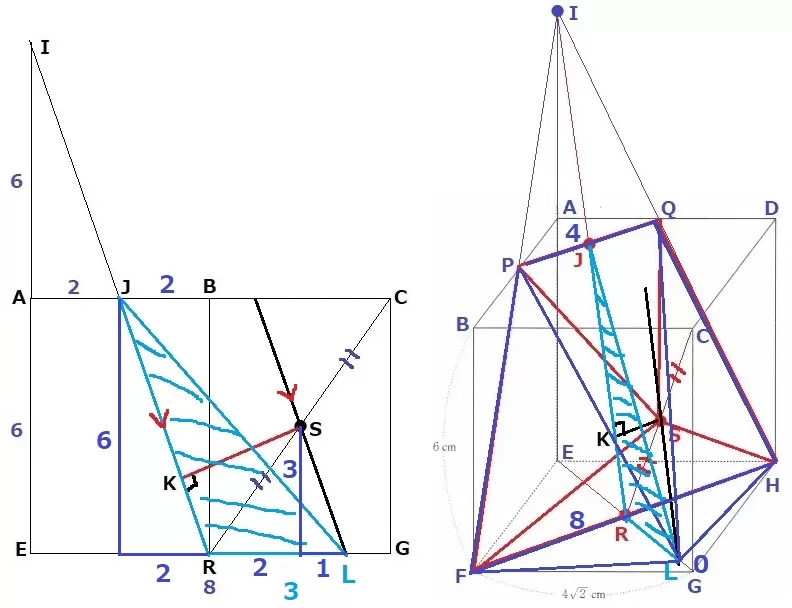
Sを通るJRに平行な線をひき、EGとの交点をLとする。
等積変形で立体L―PFHQを求めればいい。
ここで、断頭三角柱の考えを用いる。
底面は△JRL、高さはPQ・FH・Lの平均。
J→Rは下に6、右に2なので、S→Lは下に3、右に1。
ここからRL=2+1=3cmとわかる。
PQ=4cm、FH=8cm、L=0cm
3×6÷2×(4+8+0)/3=36cm3
●講評●
7割超が5%ほどしかいない。
大問1
全問死守。
大問2
(1)難しく考えない。両辺から引いたものを選ぶ。
(2)正解率7.1%!?割合計算は小学生でも解けるよ!
(3)ここも正解率が低かった。追い越しと出会いの違いに注意。
(5)直角二等辺の作図。標準レベルだが正解者は4人に1人。
大問3
(1)②0も整数である。
大問4
(2)初手は前問の答えを活用する。
大問5
ちょっと設問が酷だと思う。
大問が7つもあるのでバランスを考慮して空欄補充にするか、
証明1題であればもう少しレベルを落とした方が良い。
部分正答者は4.8%しかいなかった。
細かい部分まで説明すると冗長になりやすく、記述の工夫も問われる。
大問6
(2)②座標を文字式であらわす頻出パターン。
QRを1辺とする正方形は作図不要。QRを4倍するだけ。
大問7
(3)
…大問7個もあって最後にコレはきつくないか?
良問なので、どこか他の大問1つ削っていいと思う。



コメント