問題ＰＤＦ
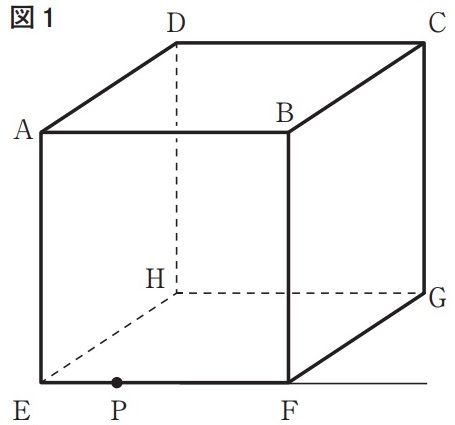
下の図１に示した立体ＡＢＣＤ―ＥＦＧＨは、１辺の長さが８ｃｍの立方体である。
辺ＥＦおよび線分ＥＦをＦの方向に延ばした直線上にある点をＰとする。
（１）
下の図２は、図１において、点Ｐと頂点Ｂ、頂点Ｂと頂点Ｇ、
頂点Ｇと点Ｐをそれぞれ結んだ場合を表している。
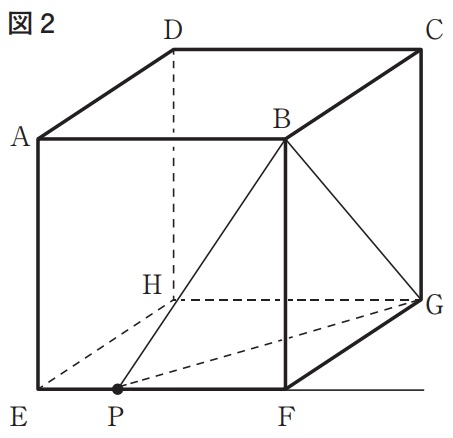
①点Ｐが辺ＥＦ上にあり、立体Ｐ―ＢＦＧの体積が立体ＡＢＣＤ―ＥＦＧＨの体積の１/10倍になるとき、ＥＰの長さは何ｃｍか。
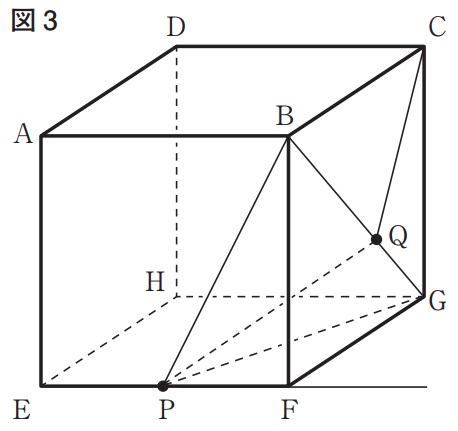
②下の図３は、図２において、ＥＰ＝４ｃｍのとき、線分ＢＧ上にあり、頂点Ｂ、頂点Ｇのいずれにも一致しない点をＱとし、点Ｐと点Ｑ、頂点Ｃと点Ｑをそれぞれ結んだ場合を表している。
ＰＱ＋ＱＣの長さが最も短くなるとき、△ＰＱＧと△ＢＱＣの面積の和は何ｃｍ2か。
ただし、答えだけでなく、答えを求める過程が分かるように、図や途中の式などもかけ。
（２）
下の図４は、図１において、ＥＰ＝24ｃｍのとき、辺ＣＤ、辺ＡＥ、辺ＦＧの中点をそれぞれＬ、Ｍ、Ｎとし、辺ＣＧ上にあり、頂点Ｃ、頂点Ｇのいずれにも一致しない点をＩとし、点Ｍと点Ｎ、点Ｎと点Ｐ、点Ｐと点Ｍ、点Ｌと点Ｍ、点Ｌと点Ｎ、点Ｌと点Ｐ、点Ｉと点Ｍ、点Ｉと点Ｌ、点Ｉと点Ｐをそれぞれ結んだ場合を表している。
立体Ｎ―ＬＭＰと立体Ｉ―ＬＭＰの体積が等しいとき、ＩＧの長さは何ｃｍか。
＠解説＠
（１）①
立方体の体積を１とすると、三角柱ＡＢＣ―ＥＦＧは１/２。
三角錐Ｂ―ＥＦＧは、１/２×１/３＝１/６
三角錘Ｂ―ＰＦＧは１/10で、これは三角錘Ｂ―ＥＦＧの１/10÷１/６＝３/５倍
２つの三角錘は高さＢＦと奥行きＦＧが共通なので、
体積比は横の長さであるＥＦ：ＰＦに相当する。
つまり、ＥＦ＝⑤とするとＰＦ＝③で、ＥＰ＝②となる。
ＥＰ＝８×②/⑤＝16/５ｃｍ
②
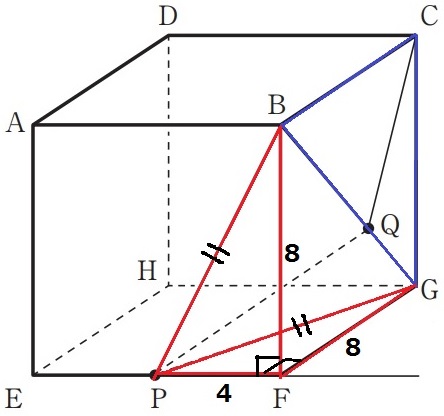
最短距離だが、面ＢＣＧと面ＢＰＧが曲がっている(;`ω´)
△ＢＣＧは正方形ＢＦＧＣの半分だから直角二等辺三角形。
△ＢＰＧはどうか。
ここで△ＢＰＦと△ＧＰＦに着目すると、
∠ＢＦＰ＝∠ＧＦＰ＝90°、ＢＦ＝ＧＦ＝８ｃｍ、共通辺ＰＦより、
２辺とあいだの角が等しいので△ＢＰＦ≡△ＧＰＦ
ＢＰ＝ＧＰだから、△ＢＰＧは二等辺三角形である。
△ＢＰＦで三平方→ＢＰ＝ＧＰ＝４√５ｃｍ
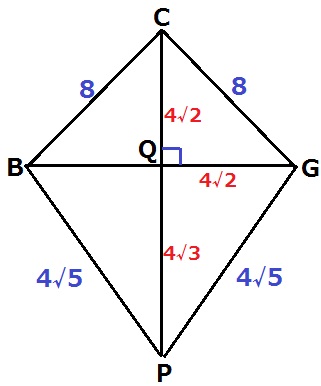
四角形ＢＰＧＣは、２つの二等辺三角形を合わせた図形。
ＣＰを対称の軸とすると左右対称であり、ＢＧ⊥ＣＰ、ＢＱ＝ＧＱ
△ＣＱＧは辺の比が１：１：√２の直角三角形だから、ＣＱ＝ＧＱ＝４√２ｃｍ
△ＰＱＧで三平方→ＱＰ＝４√３ｃｍ
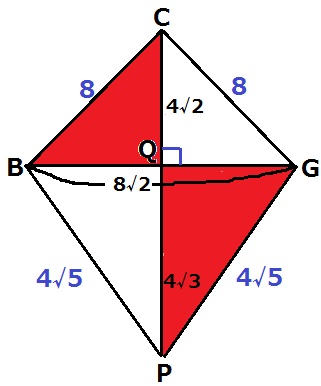
△ＰＱＧ＋△ＢＱＣは四角形ＢＰＧＣの半分である。
対角線が直交するので菱形の面積に倣って、
８√２×（４√２＋４√３）÷２÷２
＝16＋８√６ｃｍ2
（２）
難しい。
三角錘Ｎ―ＬＭＰと三角錘Ｉ―ＬＭＰは、底面が△ＬＭＰで共通。
２つの三角錘の体積が等しいから、等積変形でＩとＮは面ＬＭＰからの距離がそれぞれ等しい。
⇒ＩＮ//面ＬＭＰがいえる。まずはこれを見抜けるか。
求めたいのはＩＧ。
△ＩＮＧの各辺と平行な３直線からなる三角形は、△ＩＮＧと相似にあたる。
相似図形をどこにつくるべきか。斜辺ＩＮをポイントにすると、
Ｌを通るＩＮに平行な線をひき、ＭＰとの交点をＲ、ＩＧ//ＬＳ、ＮＧ//ＲＳとなるＳをつくる。
ＩＮ//面ＬＭＰだから、面ＬＭＰ上にあり、かつＩＮと平行であるＬＲはＭＰと交わる。
また、ＬはＤＣの中点と位置がはっきりしており、ＲＳ＝８ｃｍから、
△ＬＲＳと△ＩＮＧの相似比であるＲＳ：ＮＧ＝８：４＝２：１が利用できる。
すなわち、ＩＧ＝ＬＳ÷２
今度は手前で相似図形をつくる。
Ｒから垂線をひき、ＥＰとの交点をＴとする。
ＬがＤＣの中点⇒ＴはＥＦの中点
△ＭＥＰ∽△ＲＴＰより、ＲＴ＝４×20/24＝10/３ｃｍ
ＬＳ＝８－10/３＝14/３ｃｍ
したがって、ＩＧ＝14/３÷２＝７/３ｃｍ
国私立高校入試解説ページに戻る
コメント