問題PDF
(1)
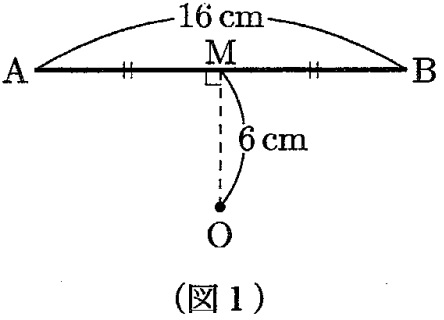
上の(図1)のように、長さ16cmのえんぴつABが机の上にあり、
ABの真ん中の点をMとします。また、MO=6cmのところに点Oがあり、
ABとMOは垂直です。このえんぴつを、点Oのまわりに机の上で1回転させたとき、
えんぴつが通ってできる図形の面積は何cm2ですか。
ただし、えんぴつの太さは考えないものとします。
以下、長方形の対角線の交点を、長方形の中心と呼ぶことにします。
(2)

上の(図2)のように、縦12cm、横16cm、わくのはば1cmの長方形の額ぶちが
机の上にあります。この額ぶちを、額ぶちの中心Oのまわりに机の上で1回転させたとき、
わくが通ってできる図形の面積は何cm2ですか。
(3)

上の(図3)のように、厚さ1cmの長方形の板を6枚組み合わせて作った、
中身が空どうの箱が机の上にあります。この箱を、上下の面の中心を通る直線を
回転の軸として机の上で1回転させたとき、
この箱の板の部分が通ってできる立体の体積は何cm3ですか。
@解説@
(1)

AOに補助線をいれると、辺の比が3:4:5の直角三角形があらわれる。
中心Oから最短は6cm、最長は10cm。
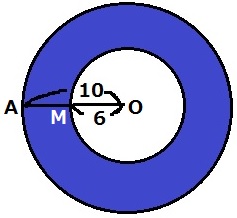
回転体は内径6cm、外径10cmのドーナツである。
(10×10-6×6)×3.14
=200.96cm2
(2)
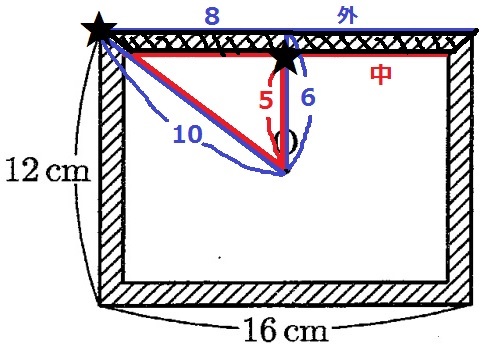
1cmの幅を考慮する。
外側の線は(1)で求めたエンピツと同じ。本問では中側の線が追加される。
額縁の上部において、中心Oから最短は5cm、最長は10cm。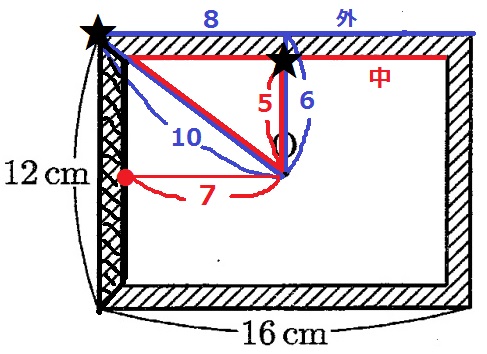
今度は枠の左部を調べてみると、最長は10cmで同じだが、最短は7cmである。
上部;5~10cm、左部:7~10cm⇒範囲は5~10cm
額物の回転体は内径5cm、外径10cmの回転体である。
(10×10-5×5)×3.14
=235.5cm2
@余談@

仮に上下の枠の幅を3cmに厚くしてみる。(左右の枠幅は4cm)
すると、(1)より外側は内径6cm~外径10cmのドーナツ。
中側は内径3cm~外側5cmのドーナツ。
このように2つのドーナツがかぶらない場合、
半径5cmより長く、6cmより短いエリアは空洞になるのでは?
と思った人がいるかもしれないが、Oから5.5cmのところ(★)は枠の中である。
結局、中の最短(最小値)~外の最長(最大値)を調べればいい。
(3)

中8cmは(2)と同じ底面積。
上下1cmずつは長方形の回転、すなわち、Oから最長10cmを半径とする円である。
235.5×8+10×10×3.14×2
=1884+628
=2512cm3



コメント