問題PDF
A君は1周3000mの池のまわりを、12時にスタート地点から一定の速さで走り出しました。
A君は1周走ったあと、スタート地点で1分休んでから1周目の速さの1.2倍の速さで2周し、
さらにスタート地点で9分休んでから1周目の速さにもどして3周すると、
合計で6周走り、走り終えた時刻は13時18分でした。
(1)
A君が1周目の速さの1.2倍の速さで2周走るときにかかった時間は、
A君がスタートしてから1周走るときにかかった時間の何倍ですか。分数で答えなさい。
(2)
1周目のA君の走る速さは分速何mですか。
B君の時計は正しくない一定の速さで進みます。
A君が1周目を走り終えたとき、B君の時計は12時15分でした。
また、A君が6周目を走り終えたとき、B君の時計は13時15分30秒でした。
(3)
B君の時計は正しい時間の何倍の速さで進みますか。分数で答えなさい。
(4)
B君の時計が正しい時刻を示したとき、その時刻を答えなさい。
またそのとき、A君はスタートしてから全部で何km走りましたか。
@解説@
(1)
速さの比は、1:1.2=5:6
時間は逆比で⑥:⑤
⑥×1周:⑤×2周=6:10=3:5
かかった時間は5/3倍。
(2)
走った時間は休憩時間をのぞくと、13:18-12:00-10分=78-10=68分
時間⑥で4周、時間⑤で2周走るので、
⑥×4+⑤×2=㉞
通常の速さで1周を走る時間は、⑥=68×⑥/㉞=12分
3000÷12=分速250m
(3)
Aが1周走り終えてから、6周走り終えるまでの時間は、78-12=66分
この間にBの時計は、13:15:30-12:15:00=1時間30秒=60.5分進んだ。
時間が進む速さの比は、正しい時計:Bの時計=66:60.5=12:11
正しい時計が⑫進むと、Bの時計は⑪進むので11/12倍。
(4)
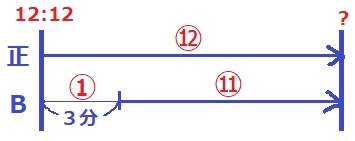
Aが1周走り終えたとき、正しい時計は12時12分、Bの時計は3分先にいる。
時間が進む比(速さの比)は、正:B=⑫:⑪
正しい時計がBの時計に追いついたとき、Bの時計が正しい時刻を示す。
このときまでに進んだ時間の比(距離の比)は速さの比と同じで、正:B=⑫:⑪
差の①が3分にあたる。
12時12分から3×⑫=36分後の12時48分にBの時計は正しい時間を指した。
Aは13時18分に6周走り終える。
13:18-12:48=30分前にAはどこを走っているか。
ラストの3周は1周12分で走るから、3周は36分間。
つまり、12時48分はAがラスト3周を走っている最中である。
残り30分間は30÷12=2.5周
Aは6-2.5=3.5周を走り終えている。
1周は3kmなので、Aが走った距離は3×3.5=10.5km
12時48分、10.5km



コメント