平均28.9点(前年比;+1.8点)
問題はこちら→東進ハイスクールさん(解答)
出題範囲の縮小はなし。
大問1(小問集合)
(1)
8+(-13)
=8-13
=-5
(2)
-6/7a÷3/5
=-10/7a
(3)
2(x+3y)-3(2x-3y)
=2x+6y-6x+9y
=-4x+15y
(4)
(3√2-√5)(√2+√5)
=6+2√10-5
=1+2√10
(5)
x2-x-12
=(x+3)(x-4)
(6)
3x2-7x+1=0
解の公式を適用して、x=(7±√37)/6
(7)
A…18/50、B…28/80=7/20
100で通分すると、A…36/100、B…35/100
Aの相対度数が大きい。
①A、②0.36
大問2(小問集合2)
(1)①
800mを20分で移動する。
a=800÷20=40
②
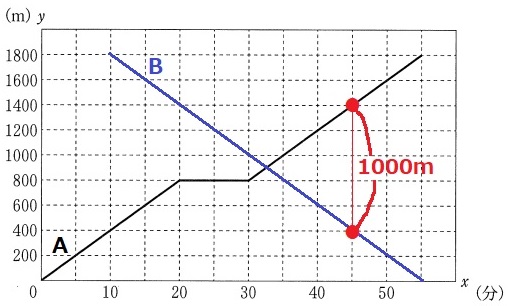
Bをグラフに記入する。
Aの傾きは右1上1、Bの傾きは右1下1(つまり速さが等しい)
格子点に注目して縦の差が1000mとなるのは10時45分。
③
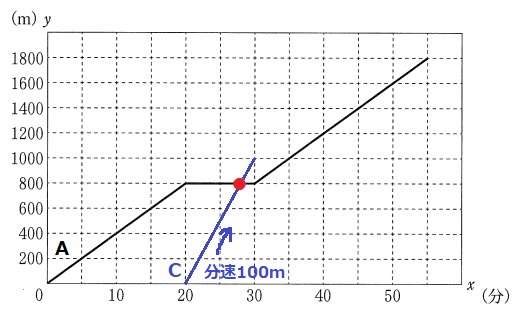
Aが休憩している800m先のQ地点でCが追いつく。
800m÷分速100m=8分後→10時28分
(2)
昨日の大人がx人、昨日の子供がy人。
1つ目は昨日の入園者数で等式…x+y=140 …①
2つ目は今日の入園料の合計で等式。
大人の入園者数は90%、子供の入園数者は105%なので、
500×0.9x+300×1.05y=52200 …②
②を整理すると、
450x+315y=52200
10x+7y=1160 …②’
①×10-②’
10x+10y=1400
-)10x+7y=1160
3y=240
y=80
①に代入。x=140-80=60
x=60、y=80
今日の大人は、60×90%=54人
今日の子供は、80×105%=84人
①…x+y、②…500×0.9x+300×1.05y
③…60、④…80、⑤…54、⑥…84
(3)①
全体⇒5×5=25通り
積が12以上⇒(3、4)(3、5)(4、3)(4、4)(4、5)
(5、3)(5、4)(5、5)
計8通り、確率は8/25
②
【少なくとも一方は奇数=全体-2つとも偶数】
2つとも偶数…2か4を2連続出す。2×2=4通り
少なくとも一方は奇数…25-4=21通り
確率は21/25
大問3(関数)
(1)
y=1/2x2にx=-2を代入。
y=1/2×(-2)2=2
A(-2、2)
(2)
y=1/2x2において、
x=0のとき、最小値y=0
x=-3のとき、最大値y=9/2
0≦y≦9/2
(3)
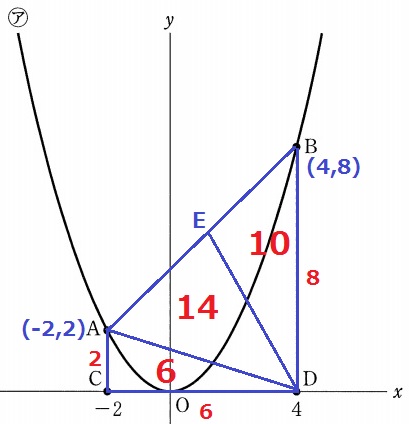
台形ACDBの面積は、(2+8)×6÷2=30
これを2:1に分けると、四角形ACDE=20、△BDE=10
△ACDは6×2÷2=6だから、△ADE=20-6=14
AE:EB=△ADE:△BDE=14:10=⑦:⑤
Eのx座標は、-2+6×⑦/⑫=3/2
Eのy座標は、2+6×⑦/⑫=11/2
E(3/2、11/2)
(4)
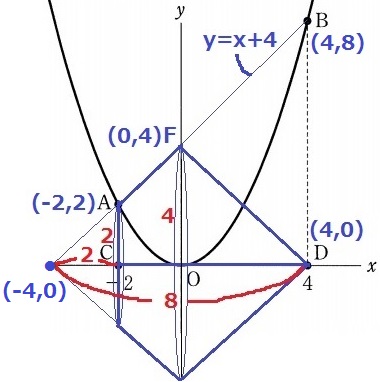
A(-2、2)→B(4、8)
右に6、上に6だから傾きは1。切片FはAから右に2、上に2で4。
AB;y=x+4はx軸と(-4、0)で交わる。
回転体の体積は、半径4cm高さの合計8cmの円錐から、半径2cm高さ2cmの円錐を引く。
4×4×π×8÷3-2×2×π×2÷3
=(128π-8π)÷3=40π
大問4(空間図形)
(1)①
AM=2cm
△ADMで三平方→DM=2√5cm
②
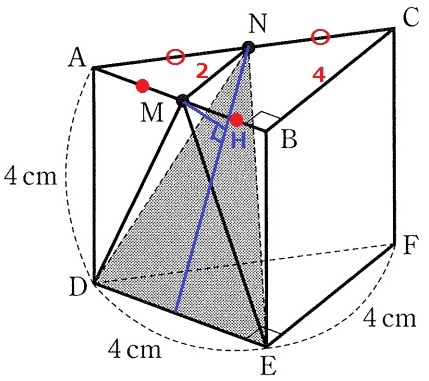
中点連結定理より、MN=4÷2=2cm
三角錐N-MDEの体積は、4×4÷2×2÷3=16/3cm3

MからDEに垂線をひき、足をIとする。
AD//MI//BEより、MはABの中点だからIもDEの中点。
MIは底辺DEを垂直に二等分するので、△MDEは二等辺三角形。
また、△MDE方向から立体をみると、MN//BCより△NDEも二等辺三角形。
(二等辺MDEで底辺DEを固定したまま、Mを奥のNに移動させるイメージ)
NHを延長したDEとの交点はIとなる。
△ADMと△MINに注目する。
AD=MI=4cm、AM=MN=2cm、∠MAD=∠NMI=90°
2辺とあいだの角が等しく、△ADM≡△MIN
前問より、NI=MD=2√5cm
△NDEの面積は、4×2√5÷2=4√5cm2
MHの長さは、16/3×3÷4√5=4√5/5cm
(2)
ここで作図問題が登場。
『半径が最も短い円』なので、直線ℓと接する接点とAが直径となる円。
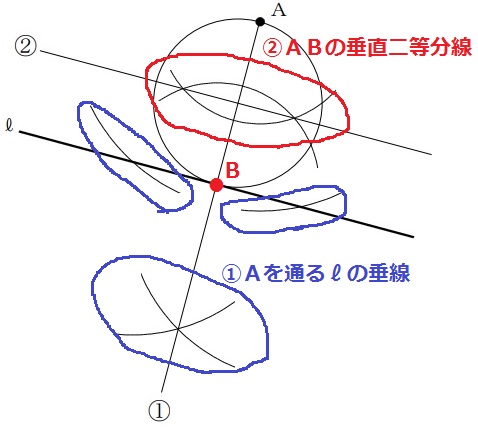
①Aを通るℓの垂線。交点が接点B。
②直径ABの垂直二等分線。中点が円の中心。
③円の作成。
大問5(平面図形)
(1)
△AGE∽△ACFの証明。
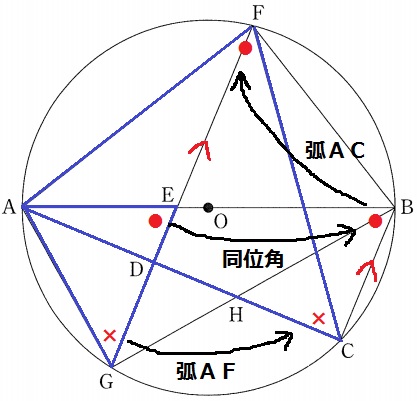
弧AFに対する円周角から、∠AGE=∠ACF
BC//FGの同位角と弧ACに対する円周角をつなげて、∠AEG=∠ABC=∠AFC
2組の角が等しいから、△AGE∽△ACF
ア…∠AGE、イ…∠ABC、ウ…2組の角
(2)
△ADG≡△BCHの証明。
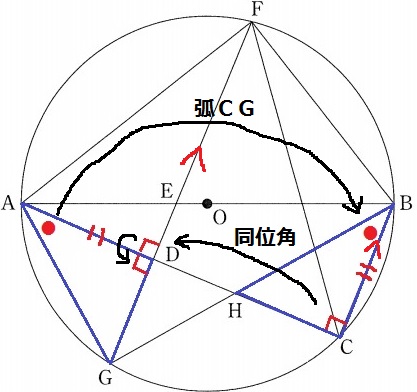
仮定よりAD=BC
この両端角を狙いにいく。
弧CGに対する円周角より、∠DAG=∠CBH
半円の弧に対する円周角から、∠BCH=90°
BC//FGの同位角で、∠FDA=90°
∠ADG=180-90=90°だから、∠ADG=∠BCH
1辺と両端角が等しく合同。
(3)①
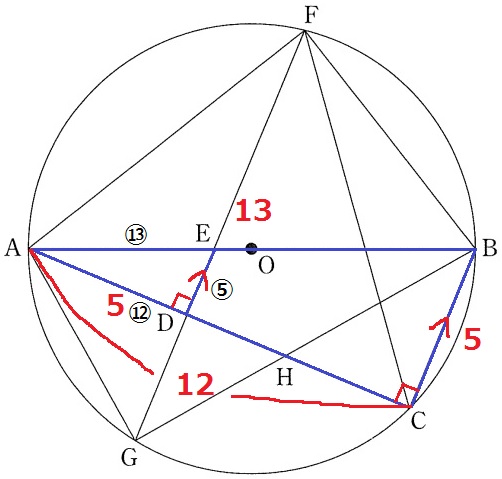
AB=13cm、BC=5cm、∠ACB=90°
△ABCは辺の比が5:12:13の直角三角形。
ED//BCより2角相等で△AED∽△ABC
前問の合同より、AD=BC=5cm
DE=5×⑤/⑫=25/12cm
②
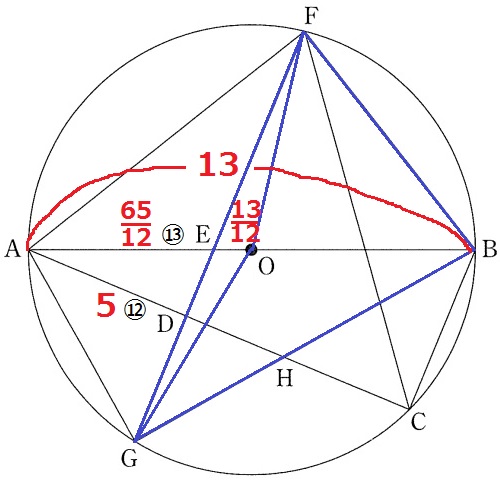
△BFGと△OFGは辺FGを共通とする。
面積比は高さの比にあたるEO:EB。
△ADEの辺の比から、AE=5×⑬/⑫=65/12cm
中心Oは直径ABの中点だから、EO=13/2-65/12=13/12cm

AE:EO=65/12:13/12=⑤:①
OB=OA=⑥
△BFG:△OFG=EB:EO=7:1
●講評●
大問1
全問とりたい。
大問2
(1)グラフを活用する。
(2)計算ミスに注意!
大問3
(3)面積を求めてAE:EBを算出。
(4)円錐の高さは合計して処理する。
大問4
(1)②三角錐N-MDEにおいて△NDEを底面とすると高さがMH。
△MDEの高さは合同を利用すると①の答えとなる。
大問5
(3)②EB:EOに着目できたかどうか。
前問の5:12:13でAEの長さがわかれば、あとは円の半径から辺の比が出せる。



コメント