問題PDF
以下の〔 〕にあてはまる数を求めなさい。
(1)
容器Aには食塩水が160g、容器Bには5%の濃度の食塩水が180g入っています。
2つの容器に入っているものと食塩10gを混ぜ合わせたところ、
容器Aにもともと入っていた食塩水の濃度と同じ〔 〕%の濃度の食塩水ができました。
(2)
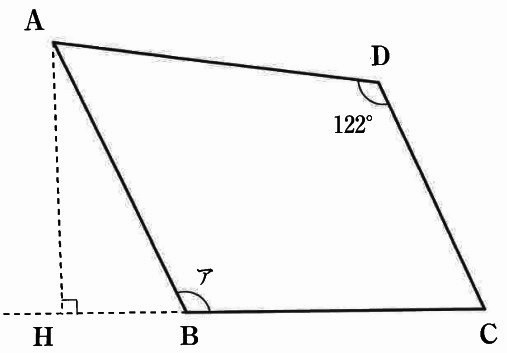
下の図のような、ABとBCの長さが等しく、ABとCDが平行である平行四辺形ABCDがあります。図のようにAHと直線BCが垂直になるように、直線BC上に点Hをとると、CDの長さがBHの長さの2倍になりました。アの角の大きさは〔 〕度です。
(3)
下の図のように四角形ABCDは正方形であり、
(ADの長さ):(CEの長さ)=12:5
となるように辺BCの上に点Eをとります。
図の〇のついた角の大きさが同じになるようにDE上に点Fをとったところ、
DFの長さが5cmになりました。四角形ABEFの面積は〔 〕cm2です。

@解説@
(1)
Aの食塩水160g、食塩は〇gとする。
Bの食塩水180g、食塩は180×5%=9g
これに食塩10gを足すと、食塩水350gで食塩は19+〇g。
この濃度がAと同じ濃度だから、
〇÷160×100=(19+〇)÷350×100
〇/160=(19+〇)/350
350×〇=160×(19+〇)
190×〇=160×19=16×190
〇=16
Aの濃度は、16÷160×100=10%
(2)
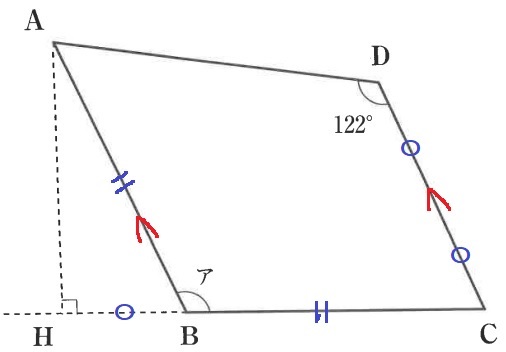
「CDがBHの2倍」が特徴的なので、これをうまく使えないか。
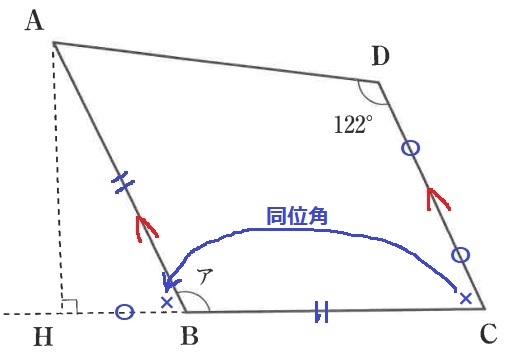
ABとDCが平行だから、同位角で∠DCB=∠ABH(×)
…なんとなくHBがCDのところに埋められそう。
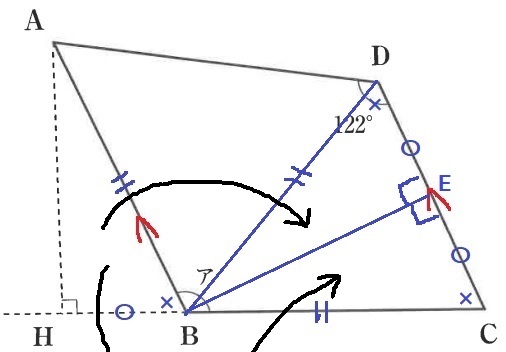
BからCDに向けて垂線、交点をEとする。
AB=BC、HB=EC、∠ABH=∠BCEで、
2辺とあいだの角度が等しいから△ABHと△BCEは合同。
さらに、BEが共通辺、CE=DE、∠BEC=∠BED=90°で、
同様に△BCEと△BDEが合同!
BC=BDより△BCDは二等辺で、∠BDC=∠BCD=×
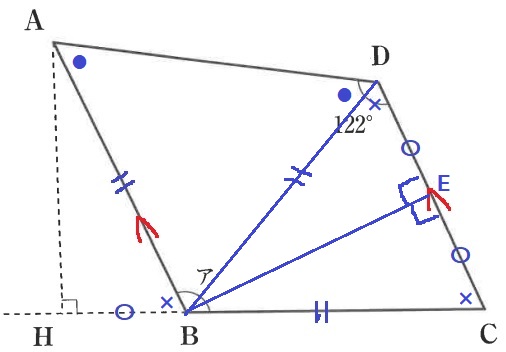
BA=BDより△BADも二等辺。
∠BDA=∠BAD=●とする。
∠ADC=●+×=122°だから、四角形ABCDの内角から、
ア=360-(●+×)×2=360-122×2=116°
(3)
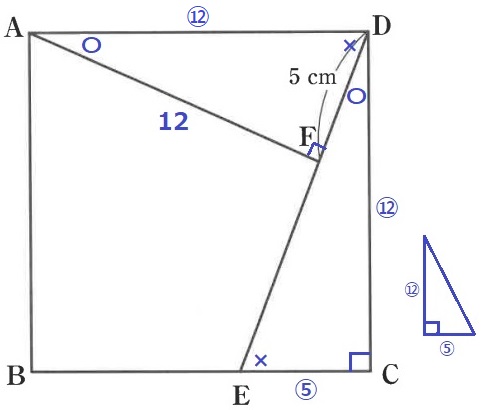
〇+×=90°の調査で、2角が等しいので△ADFと△DECが相似。
AF:FD=DC:CE=12:5
AF=12cm
△ADFの面積は、5×12÷2=30cm2
これを起点に面積比を使って展開していく。
直角三角形の斜辺以外の2辺が5:12。これを使うしかない。
また、情報が右側に偏っている点に着目する。
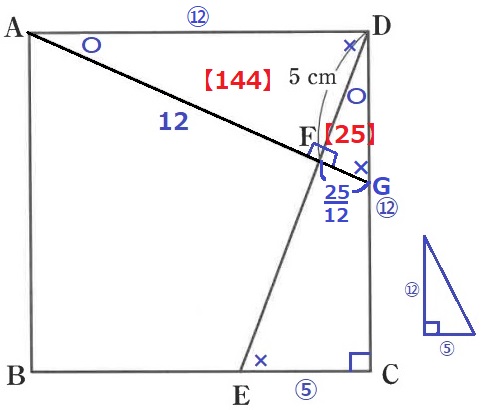
AFを延長、DCとの交点をGとする。
△DGFも内角が〇―×―90°だから、5:12の直角三角形。
FG=5×5/12=25/12cm
△ADF:△DGF=AF:FG=12:25/12=144:25

△AGDと△DECは、正方形の1辺からAD=DC、その両端角が〇と90°で等しく合同。
DG=CE=⑤
おのおのの三角形から共通部分である△DGFをひいた、残りの△ADFと四角形ECGFが等積。
四角形ECFG=144(30cm2)
先に正方形全体の面積を求めてみる。
〔△ADF→△AGD→△ACD→正方形ABCD〕
30×169/144×⑫/⑤×2=169cm2
これから、△ADFと△DGFと四角形ECFGをひく。
169-(30+30+30×25/144)
=109-125/24
=(2616-125)/24
=2491/24cm2
@余談@
 0
0
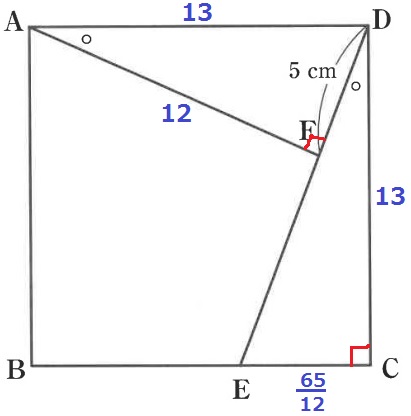
算数の世界で三平方を嫌う方もいますけど、
西大和志望者であれば5:12:13を知っている生徒もいると思うので、
それを使った方が1辺13cmがすぐ出てくるし、圧倒的に早い。
EC=13×⑤/⑫=65/12cm
13×13-5×12÷2-65/12×13÷2
=139-845/24=2491/24cm2



コメント