問題PDF
太郎くんと次郎くんは、毎週日曜日の10時にA駅を出発し、一緒にB公園まで歩きます。2人は、普段は一定の速さで歩きます。A駅からB公園まで1500mあり、途中A駅から900mのところに観覧車があります。観覧車の箱型の乗り物をゴンドラといい、ゴンドラには異なる番号が書かれています。
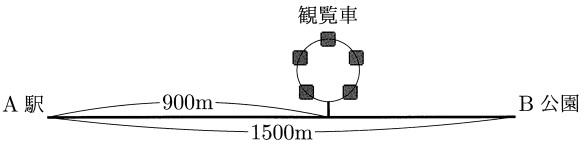
ある日曜日、次郎くんが時間通りに来なかったので、太郎くんは10時にA駅を普段の速さで出発し、観覧車に1周乗ってからB公園へ向かうことにしました。次郎くんはA駅を10時15分に出発し、普段の1.2倍の速さでB公園へ向かいました。太郎くんはゴンドラの中から次郎くんが通り過ぎたのを見たため、観覧車を降りてから普段の1.5倍の速さで追いかけたところ、普段より10分遅れて2人同時にB公園に到着しました。
B公園で遊んだ後、2人で観覧車に一緒に乗ってから帰ることにしました。観覧車から降りた後A駅へ向かって普段の速さで420m歩いたところで、どこかに忘れ物をしていることに気がつきました。太郎くんは普段の1.5倍の速さでB公園まで引き返し、B公園で忘れ物を3分探してから、そのままの速さでA駅へ向かいました。次郎くんは普段の速さのまま観覧車に戻り、2人が乗った番号のゴンドラが下に来るのを待ち、ゴンドラの中を確認してから、そのままの速さでA駅へ向かいました。次の問いに答えなさい。ただし、観覧車の乗り降りの時間や、ゴンドラの中の確認の時間は考えないものとします。
(1)
2人は普段B公園に何時何分に到着しますか。
(2)
観覧車は1周回るのに何分かかりますか。
(3)
忘れ物を確認した後、太郎くんが次郎くんに追いついたのはA駅から何mのところですか。
@解説@
(1)
次郎に注目すると、普段より15分遅れで出発して1.2倍速で歩いたら、
普段より10分遅れで到着した。
速さの比は1:1.2=5:6
時間の比は逆比で⑥:⑤(普段は⑥の時間、この日は⑤の時間かかった)
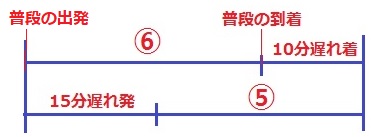
⑥+10分=⑤+15分
①=5分
⑥=30分
普段、B公園に到着する時刻は10時30分。
(2)
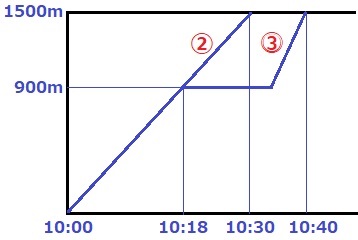
観覧車に乗った太郎に注目する。
普段の速さは、1500÷30=分速50m
観覧車まで、900÷50=18分かかった。
観覧車を降りてから1.5倍速で追いかけたので、速さの比は1:1.5=②:③
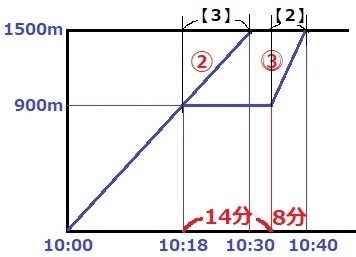
時間は逆比で【3】:【2】
【3】=10:30-10:18=12分だから、
太郎が観覧車から降りてB公園に着くまでの時間【2】=8分
観覧車の乗り降りの時間は考えないので、観覧車が1周回る時間は、
(10:40-10:18)-8=14分
(3)
問題文後半の段落。
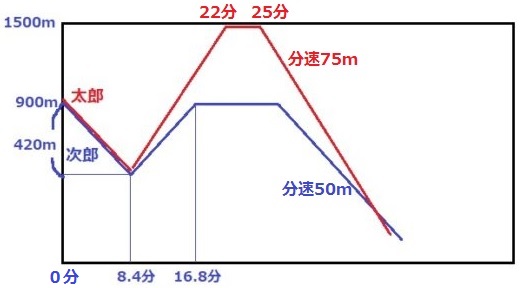
わかりやすいように最初を0分とする。
引き返した時間は、420÷50=8.4分
太郎は1.5倍速(分速75m)で戻る。
B公園に到着したのは、1020m÷75=13.6分後の22分。
3分間探し、25分にA駅へ向かう。
一方、次郎は普段の速度で引き返したので、16.8分に観覧車へ戻る。

問題は、自分たちが乗ったゴンドラが下りてくるまでの待機時間。
(2)より観覧車は14分で1周する。
ということは、観覧車を出発した0分後から14の倍数分ごとに該当のゴンドラが下にくる。
14×1分<16.8分<14×2分なので、次郎が観覧車を出発した時刻は28分。
(次郎の待機時間は、14×2-16.8=11.2分間)
このとき、太郎と次郎の距離は、(1500-900)-75×3=375m
両者は1分間で75-50=25mずつ接近するので、
375÷25=15分後に太郎が次郎に追いつく。
次郎は観覧車を出発してから900÷50=18分後にA駅に着く予定なので、残り3分。
A駅~太郎が追いついた地点までの距離は、50×3=150m



コメント