2019年度　江戸川学園取出中学過去問【算数】大問７解説

問題ＰＤＦ
次の会話文は、Ｅ中学校の２名の生徒会役員Ａ、Ｂの会話の内容です。
この会話文を読み、次の問いに答えなさい。

Ａ：これから１年生のクラスで文化祭で使う鉛筆の準備をしよう。
Ｂ：１箱に１ダース（12本）の鉛筆が入った箱をたくさん用意したよ。
Ａ：１クラスに65本ずつ必要なので、分けられるように準備を始めよう。
Ｂ：では、１箱ずつ箱を開けていき、65本より少ないときはもう１箱開け、
65本以上であるときは65本を必ず袋に入れるようにしよう。
Ａ：あと、箱から鉛筆を出すときは、12本同時に出すようにしよう。

（２人は作業を行います）

Ａ：これで17箱つかったね。いま鉛筆が入った袋はいくつあるかな？
Ｂ：【　ア　】袋あるよ。そして袋にも箱にも入っていない箱は【　イ　】本あるね。

（２人は作業を行います）

Ａ：さあ、１年生の全クラス分の袋が準備できた！
Ｂ：いま袋にも箱にも入っていない鉛筆は１本だけになったよ。
Ａ：ここまで作業してきて、袋にも箱にも入らない鉛筆が１本だけになることは初めてだね。
Ｂ：鉛筆の箱は何箱使ったかな？
Ａ：【　ウ　】箱使ったよ。
Ｂ：袋の数は全部で【　エ　】袋できたので、
これを１年生の各クラスに配って作業を終わりにしよう。

（１）
【　ア　】～【　エ　】にあてはまる整数を答えなさい。

（２）
もしこの作業を続けたとき、袋にも箱にも入っていない鉛筆が１本だけになることが何回もあります。
このときにできる袋の数に注目すると、ある条件を満たす整数になります。
その条件の【　オ　】【　カ　】にあてはまる整数を答えなさい。
ただし、【　オ　】にはできるだけ大きい整数を答えなさい。
条件：袋の数は【　オ　】でわると【　カ　】あまる整数になります。
（*実際の答案では途中経過も記述します）

ここから差がつく。
65×（袋の数）＋１＝12×（箱の数）
12の倍数より65の倍数の方が固まりが大きいので、
検討回数を少なくするために左辺から検討する。

右辺は偶数（12）をかけるので、必ず偶数になる。
左辺も偶数で偶数－奇数（１）＝奇数から、65×（袋の数）は奇数となる。
積が奇数だから（袋の数）は奇数。

先ほど、袋の数が３で鉛筆が余ったので、
今度は袋の数を５にして計算する。
65×５＋１＝326
326÷12＝27…２　←12で割り切れない！

袋の数を７にする。
65×７＋１＝456
456÷12＝38　←割り切れた！
よって、袋の数は７、鉛筆の箱は38箱。
ウ…38　エ…７

（２）
65×（袋の数）＋１＝12×（箱の数）
上の式が成り立つ条件を答える。
どうやら、袋の数をある数で割ったとき、
余りの数が何かになったときに成立するらしい…。

ポイントは、65＝60＋５＝12×５＋５に分解する。

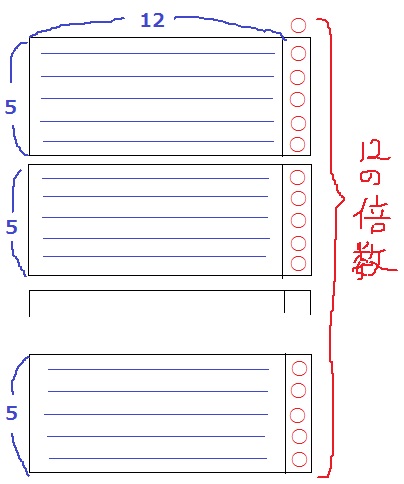
５×12の長方形は12の倍数なので、12で割り切れる。
最後の○の合計が12の倍数個になれば、全体で12で割り切れる。

１本余る鉛筆を最初の○として、65の固まりに○は５つある。
言い換えれば、１＋５×（袋の数）＝12の倍数になればいい。

前問より、袋が７つだと等式が成り立った。
１＋５×７＝36（＝12×３）
次に等式が成り立つには、袋の数を12足せば右辺が12の倍数となる。
１＋５×（７＋12）＝１＋５×19＝96（＝12×８）
袋の数に注目すると、【７、19、31、43、55・・】
７から始まり、12ずつ増える等差数列。
したがって、袋の数を12で割ると７余る整数となる。
オ…12　カ…７
難関中（算数科）解説ページに戻る