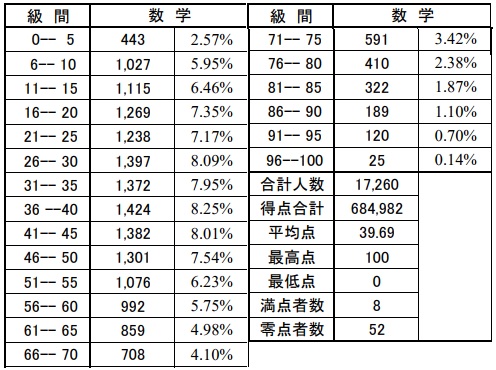
平均39.69点(前年比;-12.75点!)
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 94.0%
いろいろな情報が目に映るが、Bの得点合計-失点合計を計算するだけ。
3-7=-4
ア…-4
(2) 31.8%!

周の長さ…(縦+横)×2
(√10-√5+√5)×2=2√10m
(3) 39.2%
クリームパン5個…5a円
ジャムパン3個…3b円
これらの合計が1000円以下で購入可。
5a+3b≦1000
・・選択肢にない(つд`。)
移項して、1000-(5a+3b)≧0
ウ
(4) 63.6%
作図。教科書レベル。

線分PHが平行四辺形の高さ→Hは辺AD上にある。
Pを通るBCの垂線をひき、ADとの交点がHとなる。
大問2(小問集合2)
(1) 65.0%
連続する3つの整数の和が3の倍数である証明。
教科書に載っているので正解したい。
最も小さい整数をnとすると、連続する3つの整数はn、n+1、n+2。
n+(n+1)+(n+2)
=3n+3
=3(n+1)
n+1は整数だから、3(n+1)は3の倍数である。
ア…n+1、イ…n+2、ウ…n+1
(2) 47.5%
縦をxmとすると、横の長さはx+5m。
x(x+5)=24
x2+5x-24
=(x+8)(x-3)=0
x=-8、3
xは長さなのでx>0→x=3
縦の長さは3m。
ア…x(x+5)、イ…-8、ウ…3
(3) 48.4%
y軸についてAとBは対称である→Aのx座標は1
y=2/xに代入して、A(1、2)
これをy=ax2に代入。a=2
y=ax2について、xの値がp→qに増加するときの変化の割合はa(p+q)
2×(1+3)=8
ア…2、イ…8
(4) 40.6%
AとBの値を書いて比較すればいい。
最頻値(モード)はAが11.9秒、Bが12.0秒→Aの方が早い。
18回の中央値(メジアン)は9番目と10番目の平均。
Aが12.1秒、Bが12.0秒→Bの方が早い。
大問3(平面図形)
(1) 32.7%!
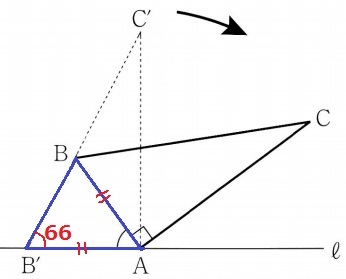
回転移動だから、AB=AB’
△ABB’は二等辺三角形。
∠BAB’=180-66×2=48°
ア…48
(2) 10.6%!
△ADB≡△AECの証明。
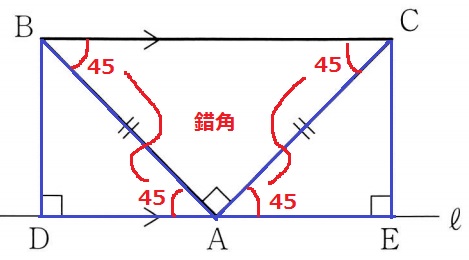
直角…∠BDA=∠CEA
斜辺…AB=AC
1鋭角…直角二等辺の45°を錯角でおろす。
斜辺と1鋭角が等しい直角三角形で合同。
(3) 5.1%!!

軌跡の問題は作図で決まる。
直角二等辺三角形をゴロンと動かしたとき、Bがどこに止まるか。
完成した図形を区切ると、半径3cm中心角90°の扇形、等辺3cmの直角二等辺、
半径3√2cm中心角135°の扇形となる。
3×3×π×90/360+3×3÷2+3√2×3√2×π×135/360
=9π+9/2cm2
ウ…9π+9/2cm
軌跡の問題は中学受験ではテッパンです。
ハイレベルな設問を置いておきますので、挑戦してみてください。

2つのパックンを回転移動させます。

軌跡の形から回転図形を探る変わった設問でした。

線分の軌跡。やや難問ですが、これができれば軌跡の問題はだいたい大丈夫です。
大問4(数量変化)
(1) 41.9%
20時間後の200Lから「ある時刻」にさかのぼる。
200L+30L×20時間=800L
(2) 6.9%!!
補給している時間は、35-20=15時間
この間に、1700L-200L=1500L増加している。
1時間あたりの増加量は、1500L÷15時間=100L
留意点は、燃料が補給されている間も自動運転をしているので、
1時間あたり30Lの燃料Aが消費されつづけていること。
-30Lを使いつつ+100L増えたから、1時間あたりの補給量は130L
(3) 18.0%!
燃料Bに関する新たな情報は、『80時間後にAはBより700L少なかった』
80時間後のAの残量を求める。
1700L-30L×(80-35)時間=350L
80時間後のBは、350+700=1050L
80時間でBは1450-1050=400L消費している。
1450-200=1250L消費するには、80時間×1250/400=250時間後
大問5(確率)
(1)① 58.5%
Eに止まるには、aとbの和が4か12。
◆a+b=4
(1、3)(3、1)(2、2)
◆a+b=12
(6、6)
計4通り
確率は、4/36=1/9
② 23.0%!
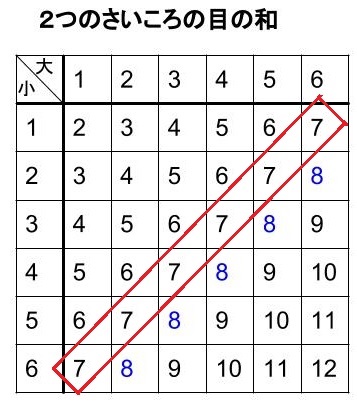
中学数学の無料オンライン学習サイトchu-su-より。
7を境に、左上と右下の個数が対称。
表を参考にして、各マスに止まる場合の数を求める。
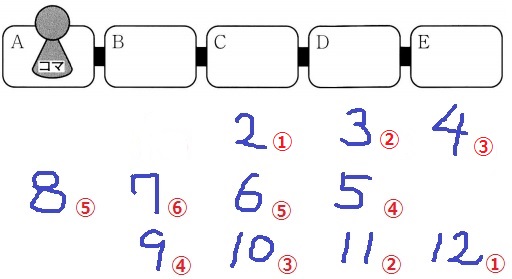
Bが10通りで最も出やすい。
確率は、10/36=5/18
B、5/18
(2) 21.6%!

8マス動かすとコマがAに戻る。
⇒8マスを1ループと考えると、8で割った余りで場所が特定できる。
4の5乗➡45=(22)5=210
8=23
210÷23は割り切れる→余り0→A
大問6(空間図形)
(1) 18.9%!

△ABCで三平方→辺の比は3:4:5で、CB=15cm
組み立てるとCBとCDが接する。
△CDEの面積は、5×15÷2=75/2cm2
ア…75/2
(2) 15.7%!

↑これをイメージできるか否か。
DとFがBと重なる。
面(え)を底面とすると、これと垂直なのは面(あ)と面(う)
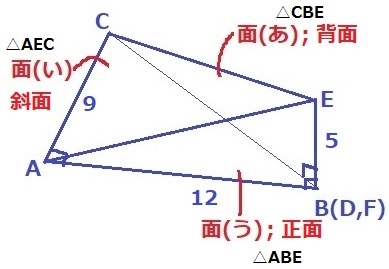
体積は、△ABC×EB÷3
=9×12÷2×5÷3=90cm3
イ…面(あ)・面(う)、ウ…90
(3) 23.0%!
三角錐の体積は、底面積×高さ÷3
高さが最も長い…底面積が最も小さい。
高さが最も短い…底面積が最も大きい。

EF=5cm、FA=12cm
△AEFは辺の比が5:12:13の直角三角形→EA=13cm
(あ)と(う)を比べると高さが5cmで共通だから、底辺のDCとFAを比べる。
DC>FA→最も底面積が小さい=最も高さが長くなるのは面(う)
(い)と(え)を比べると高さが9cmで共通だから、底辺のEAとABと比べる。
EA>AB→最も底面積が大きい=最も高さが短くなるのは面(い)
エ…面(う)、オ…面(い)
●講評●
大問1
(1)計算は瞬時に終わるが、紙をめくっていきなり表が飛び込んでくると焦る。
(2)まずは落ち着くこと。
(3)よくある式がない。冷静に。
大問2
基本レベル。
(4)説明問題だが、数値を比較してどっちが早いかを書くだけ。
大問3
(3)
中学受験では基礎レベル。公立勢も奮闘したい。
軌跡の問題はイメージ。そして作図。できた図形をうまく切り分ける。
大問4
数学というより算数。
大問5
(2)ここで整数問題が絡む。
1ループはいくつか。8コマ進むとスタートのAに戻る。
大問6
(2)組み立て予想図を描こう。
どことどこの辺がくっつくか。4面しかないので誘導を手がかりに正解したい。
(3)底面積と高さは反比例。長さの数値も整数でやりやすかった。
平均40切っただと・・?(゚言゚)


コメント