2021年度　宮城県公立高校入試問題過去問【数学】解説

平均47.6点（前年比；＋3.1点）
最高点100点、最低点０点
問題はこちら→ＰＤＦファイル
出題範囲の除外は標本調査。

大問１（小問集合）

（１）
－14－（－５）
＝－14＋５
＝－９

（２）
３/２÷（－１/４）
＝－６

（３）
２ａ²ｂ³÷ａｂ
＝２ａｂ²　←代入
＝２×３×（－２）²
＝24

（４）
４ａ－５ｂ＝３ｃ
４ａ＝５ｂ＋３ｃ
ａ＝５/４ｂ＋３/４ｃ

（５）
√27＋３/√３
＝３√３＋√３
＝４√３

（６）
ｘ²－25ｙ²
＝（ｘ＋５ｙ）（ｘ－５ｙ）

（７）
ア：０分以上60分未満の８人に０分がいるかもしれない。×
イ：最頻値（モード）は60～120の階級値である90分。〇
ウ：階級値×度数の合計を40で割る…。
（30×８＋90×13＋150×11＋210×６＋270×２）÷40＝4860÷40＝121.5×
エ：40人の中央値（メジアン）は20番目と21番目の平均。60～120の階級×
オ：２÷40＝0.05〇
イ・オ

（８）

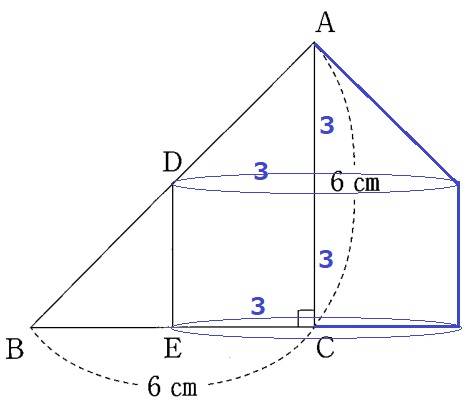
円柱に円錐が乗っかる立体になる。
３×３×π×３＋３×３×π×３×１/３
＝36πｃｍ³

大問２（小問集合２）

（１）①
十の位がａ、一の位がｂの自然数Ｐ。
Ｐ＝10ａ＋ｂ

②
Ｑ＝10ｂ＋ａ
Ｐ－Ｑ
＝（10ａ＋ｂ）－（10ｂ＋ａ）
＝９ａ－９ｂ
＝９（ａ－ｂ）＝63
ａ－ｂ＝７
ａ＝ｂ＋７

Ｐは奇数なので、一の位のｂは奇数。
ｂが３以上だと、ａが10以上になってしまうので不適×。
ｂ＝１
ａ＝１＋７＝８
Ｐ…81

（２）①
１回ルーレットを回して、ＢからＣに球が１個移動する。
→３を出す。
確率は１/４

②
余事象。
『少なくともＣに１個ある』→全体からＣが０個の確率を引く。
Ｃに球を移さないようにするには３を出さない。
１・２・４を２回出す。
Ｃに球が０個…３/４×３/４＝９/16
Ｃに球が少なくとも１個…１－９/16＝７/16

②
Ｂから左に１、上に１移動すると切片は２。
ＡＢ；ｙ＝－ｘ＋２
これにｙ＝－２を代入→Ｃ（４、－２）
今度はｙ＝ａｘ²に放り込む。
－２＝４²ａ
ａ＝－１/８

（４）①
最後の一文『ＢはＡの半分の箱数、ＣはＢの３倍の箱数』
連比処理。
Ａ：Ｂ：Ｃ
２：１
　　１：３
２：１：３
Ａの箱数をｘとすると、Ｃは３/２ｘ。

②
前問ではＡの箱数をｘとしたが、最も少ないＢの箱数をｘとした方が計算が楽。
各々の箱数は、Ａ…２ｘ、Ｂ…ｘ、Ｃ…３ｘ
ドーナツの数で等式を立てる。
２×２ｘ＋４ｘ＋３ｘ＝176
11ｘ＝176
ｘ＝16

Ａ…32箱、Ｂ…16箱、Ｃ…48箱
カップケーキの個数は、
１×32＋２×16＋２×48
＝32＋32＋96＝160個

大問３（関数）

（１）
傾きａを大きくするとグラフは急勾配になり、ｙ軸に接近する。
ウ

（２）①
ＯＡを斜辺とする直角三角形をつくる。
辺の比は３：４：５でＯＡ＝５

②
O→Ａ；右に３、上に４移動するので傾きは４/３。
ｙ＝４/３ｘ＋ｂ
（ｘ、ｙ）＝（５、０）を代入。
０＝４/３×５＋ｂ
ｂ＝－20/３
ｙ＝４/３ｘ－20/３

③

Ａを通るｘ軸に平行な線をひき、ℓとの交点をＤとする。
四角形ＡＯＢＤは２組の対辺が平行である平行四辺形。
△ＡＯＢの面積…５×４÷２＝10
△ＡＯＢ≡△ＡＤＢより、△ＡＤＢの面積も10。
△ＡＢＣの面積…10÷２＝５
△ＡＣＤの面積…10－５＝５
ＢＣ：ＣＤ＝△ＡＢＣ：△ＡＣＤ＝１：１
すなわち、ＣはＢＤの中点にある。
ＢとＤのｘ座標とｙ座標の平均がＣ座標となる。
Ｃ（13/２、２）

④
問題集によくある形式なので解けるようにしておきたい。

ＡＰ＋ＰＢが最短距離になる。
Ｂをｙ軸について対称移動させた点をＢ’とし、ＡＢ’を結ぶ。
この切片がＰとなる。
三角形の相似から、Ｐのｙ座標は４×５/８＝５/２

大問４（平面図形）

（１）
△ＡＣＤ∽△ＥＣＡの証明。

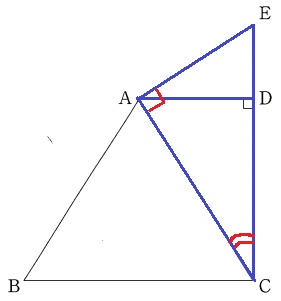
仮定の直角＋共通角→２角相等で∽。

（２）①

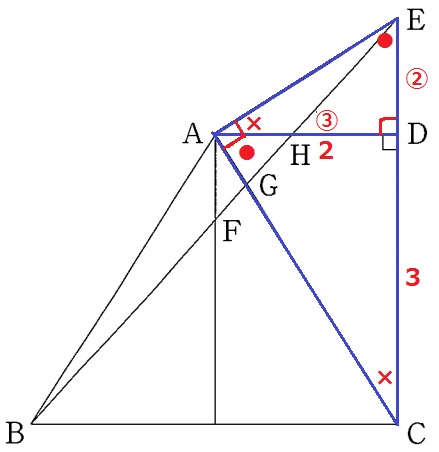
●＋×＝90°で角度を調べていくと、２角相等で△ＡＣＤ∽△ＥＡＤ
ＡＤ：ＤＥ＝ＣＤ：ＤＡ＝③：②
ＥＤ＝２×②/③＝４/３ｃｍ

②

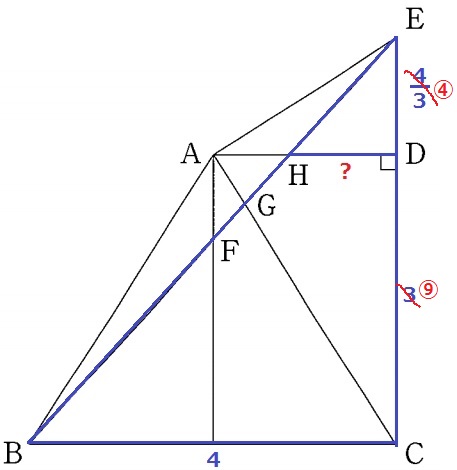
ＥＤ：ＤＣ＝４/３：３＝④：⑨
△ＥＨＤ∽△ＥＢＣより、ＢＣ：ＨＤ＝ＥＣ：ＥＤ＝⑬：④
ＨＤ＝４×④/⑬＝16/13ｃｍ
△ＥＨＤの面積は、16/13×４/３÷２＝32/39ｃｍ²

③

ＦＨとＧＨを１辺とする三角形に着目する。
ＧからＡＨに向けて垂線、交点をＩとすると、△ＡＦＨ：△ＩＧＨの相似比がＦＨ：ＧＨである。

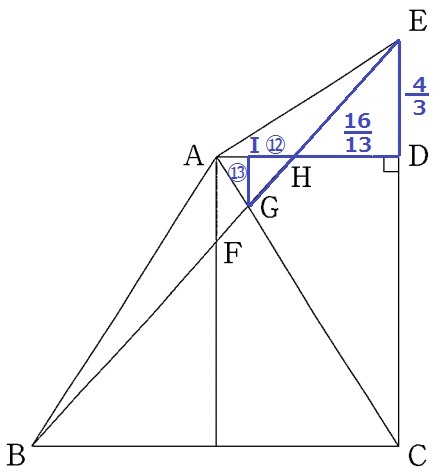
△ＥＤＨ∽ＧＩＨ。
前問の数値が利用できる。
ＩＧ：ＩＨ＝ＤＥ：ＤＨ＝４/３：16/13＝⑬：⑫

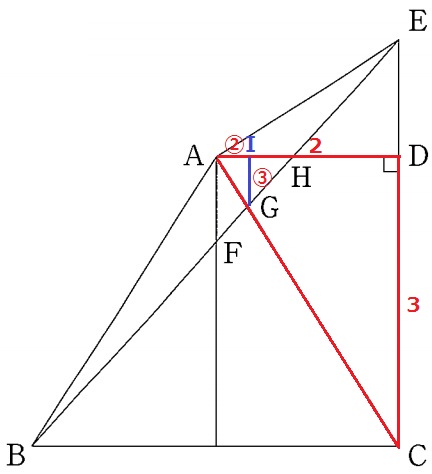
次は△ＡＩＧ∽△ＡＤＣ
ＡＩ：ＩＧ＝ＡＤ：ＤＣ＝②：③

Ｉ周辺をピックアップします。
③＝⑬なので、赤を13倍、青を３倍すれば比を統一できる。

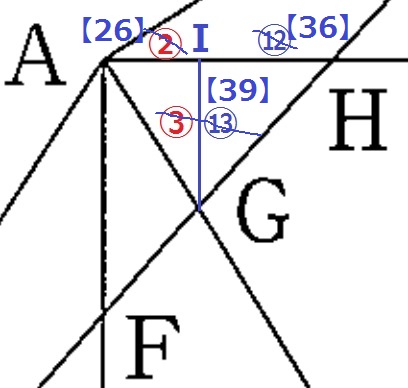
↑こうなりました。
ＡＩ：ＩＨ＝26：36＝13：18

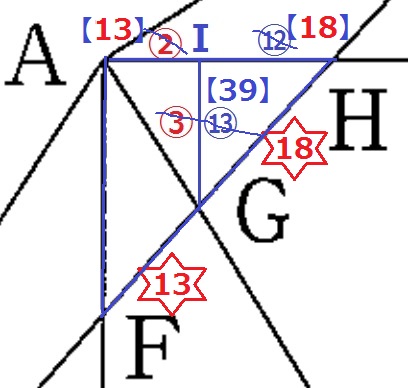
最後に△ＡＦＨ∽△ＩＧＨ
ＦＨ：ＧＨ＝31：18