平均42.1点(前年比;+3.0点)

問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 67.6%
-11+6
=-5
(2) 80.5%
7/4a-3/5a
=23/20a
(3) 81.9%
2x-3y=1 …①
3x+2y=8 …②
①×3-②×2
6x-9y=3
-)6x+4y=16
-13y=-13
y=1
①に代入。2x-3=1
x=2
x=2、y=1
(4) 69.6%
√3(2-√6)
=2√3-√18
=2√3-3√2
(5) 78.7%
x2-7x+12
=(x-3)(x-4)=0
x=3、4
(6) 64.3%
x3×(6xy)2÷(-3x2y)
=x3×36x2y2÷(-3x2y)
=-12x3y
(7) 42.5%
yの変域が0以上なので、グラフは下に凸。
x=-3のとき、最大値y=1
これをy=ax2に代入。
1=(-3)2a
a=1/9
(8) 76.6%
最頻値(モード)…最もあらわれている値。
7点
(9) 16.6%!
△DFCと面積の等しい三角形は3つある。

AD//BCより、△DFC=△AFC
AC//EFより、△AFC=△AEC
さらに、AB//DCより、△AEC=△AED
等積変形後の三角形から、さらに連鎖してつなげていく。
△AFC・△AEC・△AED
(CとF)(CとE)(DとE)計3通り
4枚から2枚選ぶ→4C2=6通り
確率は、3/6=1/2
大問2(数量変化)
(1) 68.4%
適切な情報を拾い上げること!
旅行会社の売り上げの式はy=5000x
y=5000×15=75000円
(2) 34.1%
売上はy=5000x
費用はy=1900x+8万
損益分岐点は売上=費用となる。
5000x=1900x+8万
3100x=80000
x=25.8…
26人以上であれば売上>費用となり、利益がでる。
(3) 23.6%!
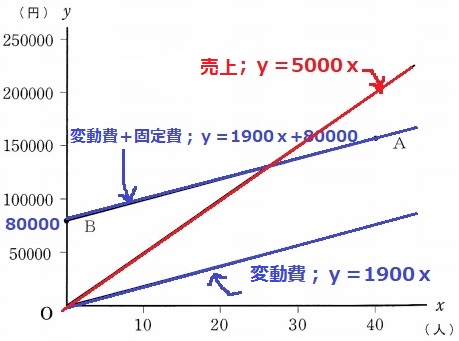
弁当代・土産代・入場料は人数に応じて変動する変動費。
バス代は人数に関係なく、一定の固定費。
A、Bを含む直線は費用の合計(変動費+固定費)を表したもの。
(赤線は売り上げで、交点のx座標が前問の25.8…にあたる)
Aは40人の費用(変動費+固定費)
Bは0人の費用(固定費)
この差は40人分の変動費となる。エ
(4) 15.7%!
説明問題。
45人分の費用は、1900×45+8万=165500円
売上=費用+利益
売上=165500+10万=265500円
これを45で割れば1人あたりの売上、すなわち、1人あたりの参加費となる。
265500÷45=5900円
1人あたりの参加費を5900円以上にすれば、100000円以上の利益を出せる。
@別解@
1人あたりの参加費で、1人あたりの変動費を除くと、
固定費8万+利益10万=18万円を45人で負担すればいい。
180000÷45=4000円
これに変動費1900円を足して、1人あたりの参加費は5900円。
大問3(平面図形1)
(1) 32.8%!
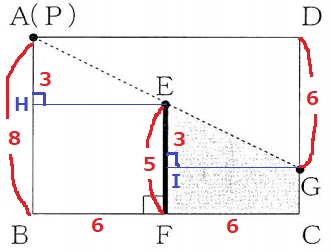
A→E→Gと下がっていくとき、A→Eで3cm下がる。
FはBCの中点なので、EはAGの中点。
E→Gでも同様に3cm下がる。
CG=8-6=2m

GがDに重なったときの様子。
先ほどの図を左右反転させたのと同じ。
AP=6m
(2) 17.3%!
△PFEと△GHEの証明。
対頂角と錯角で2角相等→∽
(3) 0.7%!!!
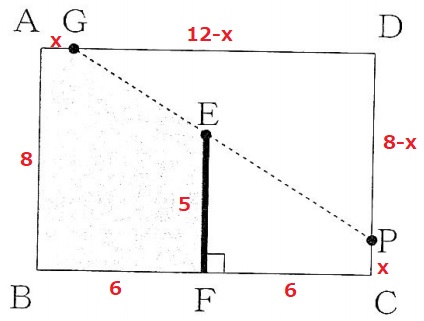
求めたいCPをxとする。
文字について解くには、式に定数項が欲しい。
xを含まない数で使えそうなところは横の辺である6
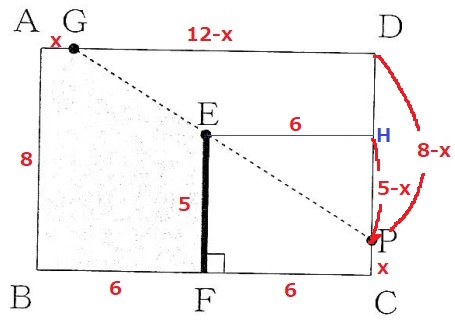
Eを通るBCに平行な線をひき、DCとの交点をHとする。
△EHP∽△GDPを利用して比例式を作る。
EH:HP=GD:DP
6:(5-x)=(12-x):8-x
外項と内項の積より、
6(8-x)=(5-x)(12-x)
48-6x=60-17x+x2
x2-11x+12=0
解の公式を適用する。
x=(11±√73)/2
CP<CDゆえ、0<x<8
√64<√73<√81より、√73の整数部分は8。
x=(11+√73)/2では、(11+8…)÷2=19…÷2=9…となり、
8を超えるので条件に適合しない。
x=(11-√73)/2は条件に適合。
CP=(11-√73)/2m
大問4(平面図形2)
(1) 5.1%!!
円を3等分することができる理由説明。
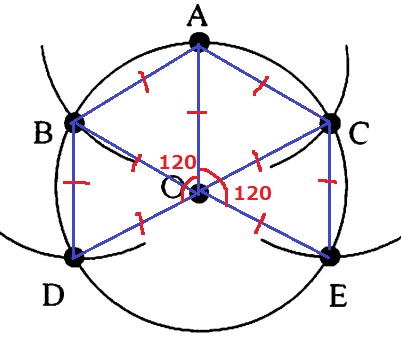
3等分の説明は、弧の長さが円周の3分の1か、扇形の中心角が360÷3=120°か。
円の下(Aの反対側)に点がないので弧の長さではなく、中心角から攻める。
すなわち、∠AOD(∠AOE)が120°である点を指摘すればいい。
図中の4つの三角形は、半径と半径と同じ長さをゆえ、いずれも3辺が等しく正三角形。
ここから内角の60°を2倍して、∠AOD=∠AOE=∠DOE=120°となる。
中心角が120/360=1/3だから、円の面積を3等分する。
(2) 17.4%!
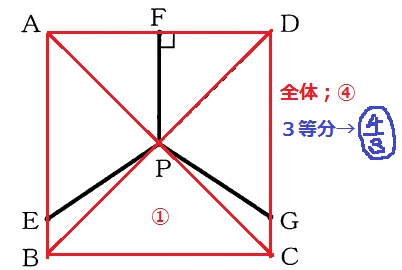
正方形を4等分したうちの1つ(△ABPなど)の面積を①とする。
全体の正方形ABCDは④。これを3等分すると〇4/3。
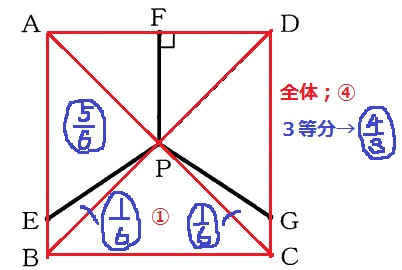
五角形PEBCGの面積が〇4/3なので、
それから△PBCをひき、左右対称から÷2をすると△PEBの面積が得られる。
△PEB…(〇4/3-①)÷2=〇1/6
△PAE…①-〇1/6=〇5/6
AE:EB=△PAE:△PEB=5/6:1/6=5:1
(3) 0.2%!!!
ラストに作図問題が登場。
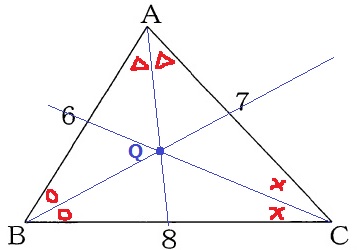
『△ABC内部に各辺から等しい距離にある点Q』
2直線からの距離が等しい→角の二等分線
この交点が点Qとなる。
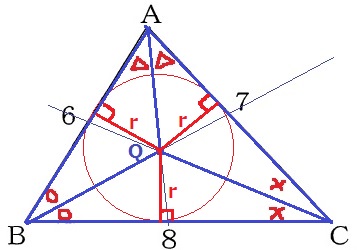
Qはいわゆる内心で、内接円の中心点である。
三角形の各辺と内接円の半径rは垂直に交わる(接線と半径は直交)
△ABQと△BCQと△CAQは高さがrで共通しており、
底辺の長さである6:8:7が3つの三角形の面積比となる。
ということは、底辺の長さを等しくすれば、各々の面積が等しくなる。

(↑Qを内心Iにしてしまいました…)
△ABCの周りの長さは、6+8+7=21cm
その3等分は、21÷3=7cm
底辺の長さを7cmにする。
留意すべき点は、Eは辺BC上、Fは辺CA上の点であること!
BE=7cmはACの長さを、CF=6cmはABの長さをとればいい。
手順をまとめると、、
①角の二等分線を2本、その交点をQとする。
②ACの長さをとり、BからEを作る。
③ABの長さをとり、CからFを作る。
④線分BQ、EQ、FQをひき、△ABCを3等分する。
@余談@
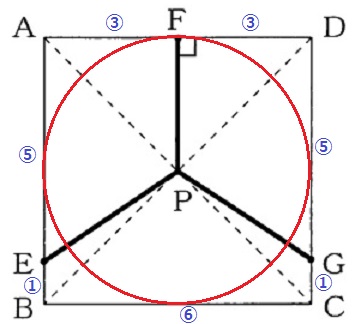
(2)は三角形ではなく正方形だが、内接円の中心がPとなるので、
これも底辺の長さの比から面積の等分を考えることができる。
●講評●
30~49点が40%以上も占め、得点分布が左に寄っている。
ヤバそうに感じたら、とれるところを安全にとっていこう。
大問1
(1)単純な正負の数だが、いきなり文章題が出されてうろたえたのか、正解率は7割を切る。
(7)基礎的な計算問題は解けているので、変域問題もいけるはず。
(9)3つすべての三角形を見つけるには、奥の奥まで手を伸ばす必要があった。
大問2
全体的に正答率が良くない。原因は文章題に対する苦手意識か。
当たり前だが、文章を大雑把に斜め読みするのは×。
社会科の資料問題と同様、必要な情報だけを抜き取ること。
計算は【売上=費用(固定費+変動費)+利益】の関係性を一次関数に乗せればいい。
似たような問題が学校か塾の問題集にあると思う。
大問3
後半の平面図形。シンプルな図形だが、やりづらさがあったか。
(2)証明はもっとできたはず。
前問がわからなくても解ける。
(3)立式は長さが整数値である辺をうまく使う。
情報が足りなかったら補助線。どこで相似を編み出すか。
大問4
こちらも独特でした。しかも、連続で平面が狙い撃ち・・。
(3)正解率0.2%の難問。
すべて三等分の問題なので、前問をどう使うかが鍵となった。
Qが内心→内接円でおなじみの3つの三角形→底辺に応じた変形
以下、公式の講評より。
『三角形の高さと内接円の半径の関係や三角形の面積と底辺の長さの関係に着目し作図する問題の正答率が特に低かった。作図や図形に関する知識をただ活用するのではなく、題意を正確に読み取り、数学的に考察し必要に応じて活用する力の育成が望まれる』



コメント