2019年度　甲陽学院中学２日目過去問【算数】大問４解説

問題ＰＤＦ
１辺が４ｃｍの正方形８個を用いて図のような長方形を作りました。

始めに、正方形の対角線の長さの細い棒がＡＢにあって、その棒を次の操作で順に動かしました。
操作①　Ｄを中心に、ＢＣの位置まで右回りに90°回転させる。
操作②　ＢＣの位置からＤＥの位置まで平行に動かす。
操作③　ＤＥの位置からＦを中心に右回りに90°回転させる。

（１）
操作①で棒が通過した部分の面積を求めなさい。

（２）
操作①、②、③で棒が通過したすべての部分の面積を求めなさい。

（１）

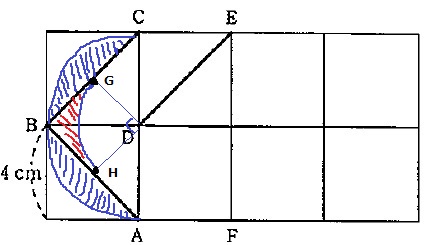
ＡはＢに、ＢはＣに移動する。
ＢＣとＡＢの中点をそれぞれＧ・Ｈとする。
線分ＡＢとＤの距離であるＨＤがＧＤへ移動。
斜線のエリアが求積すべき範囲となる。
青…半円－直角二等辺＝４×４×3.14×１/２－８×４×１/２＝9.12ｃｍ²
赤…半径ＤHの長さは根号を用いるので小学生は求められないが、
ＤH＝□とすると、□×□は正方形ＢＨＤＧの面積となる。
ＢＨＤＧ＝４×４÷２＝８ｃｍ²
８－８×3.14×１/４＝1.72ｃｍ²
したがって、9.12＋1.72＝10.84ｃｍ²

（２）
操作手順ごとに作図する。

複雑な図形を手ごろな形に区分けする。

右側は移植して、半径８ｃｍの扇形から半径ＦＩの扇形を引けばいい。
半径ＦＩの２乗は、前問のように正方形（ＥＤＦＩ）の面積を使う。
左下は（１）の半分。
10.84÷２＋４×４×3.14×１/４＋４×４×１/２＋８×８×3.14×１/４－８×８÷２×3.14×１/４
＝5.42＋４×3.14＋８＋16×3.14－８×3.14
＝13.42＋（４＋16－８）×3.14
＝13.42＋37.68＝51.1ｃｍ²
全体の長方形から周りの白をひいても出せます。
難関中（算数科）解説ページに戻る