平均54.3点(前年比;+0.7点)
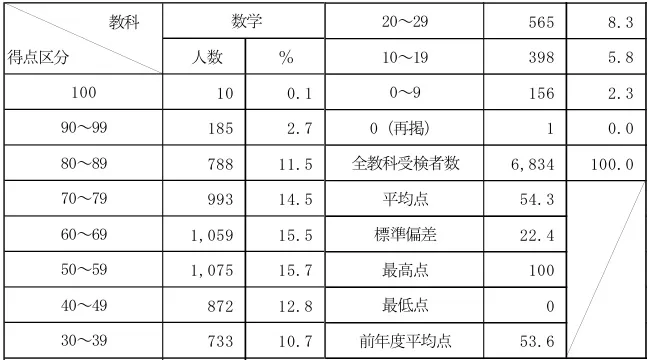
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1)ア 95.6%
4-(-1)
=4+1
=5
イ 95.5%
8×(-3)÷4
=-6
ウ 68.7%
(9x-6y)÷(-3/2)
=9x×(-2/3)-6y×(-2/3)
=-6x+4y
エ 66.5%
(2x+y-1)/3-(3x-2y+3)/5
={5(2x+y-1)-3(3x-2y+3)}/15
=(10x+5y-5-9x+6y-9)/15
=(x+11y-14)/15
オ 60.5%
(√6+√2)(√24-√8)
=√2(√3+1)√8(√3-1) ←(√3+1)(√3-1)=(√3)2-12
=4(3-1)
=8
(2) 71.4%
3+4=7
3-4=-1
-1、7
(3) 71.8%
取り出した35個のうち、全体:印付き=㉟:②
印付きは全部で24個だから、全体は24×㉟/②=420個
(4) 62.9%
(1/3x+3)2
=1/9x2+2×1/3×3x+9
=1/9x2+2x+9
(5)a…66.9%、b…33.1%!
y=x2において最大値y=16のとき、x=±4
x≧-3だからx=4→a=4
グラフは原点を通過するので、最小値b=0
a…4、b…0
(6) 76.8%
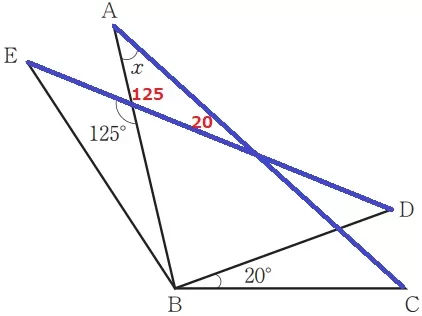
△ABC≡△EBD
Bを回転の中心として△ABCを反時計回りに20°回転すると△EBD。
→対応する辺であるACとEDがなす角は20°
125°を対頂角で移し、x=180-(125+20)=35°
(7) 42.5%
命題【x=3、y=1 → x+y=4】
逆【x+y=4 → x=3、y=1】
仮定と結論を入れ替えたものを逆といい、
逆は必ずしも正しくはなく、上の逆は正しくない。
和が4となる別の組み合わせ(反例)を挙げればいい。
(解答例)
x=2、y=2
x=-1、y=5
(8) 39.5%
ア:『xの値を1つ決めると、それに対応してyの値がただ1つに決まる』
→xに何かを代入すればyの値は1つだけ=yはxの関数である。〇
イ:方程式が1つしかないので解は無数にある(不定)。〇
ウ:2x+y=3にx=1、y=1を代入すると3になる。〇
エ:yについて解くと、y=-2x+3。傾きは-2×
エ
大問2(データの活用・方程式)
(1)ア 80.1%
35人の中央値は18番目の値。
15分以上20分未満の階級に含まれる。
イ 66.5%

1:Xの15分未満は、1+3+5=9人×
2:25~30分の階級に度数があるYの方が最大値は大きい。×
3:Xは4/20=1/5、Yは7/35=1/5で等しい。〇
4:余事象のように〔全体-20分以上=20分未満〕で求める。
Xの20分未満…(20-4)/20=4/5、Yの20分未満…(35-7-3)/35=5/7
Xの方が大きい。×
3
(2)ア あ…67.4%、い…65.3%、う…42.3%
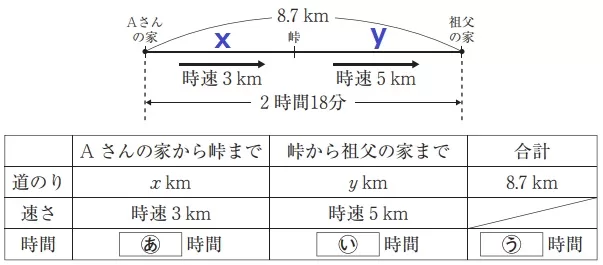
時間=道のり÷速さ
あ…x/3、い…y/5
@@
2時間18分=2・18/60=2・3/10=2.3時間
う…2.3
イ 28.7%!
道のりで等式。
x+y=8.7 …①
時間で等式。
x/3+y/5=2.3 ←30倍
10x+6y=69 …②
①×10-②より、4y=18
y=4.5
①より、x=8.7-4.5=4.2
A家~峠…4.2km、峠~祖父家…4.5km
大問3(図形)
イ 42.2%
側面の扇形の中心角は、360×半径/母線
=360×1/3=120°
ウ 1.0%!!!
120°を活用する。

Mから垂線をおろし、BAの延長との交点をNとする。
△AMNは内角から辺の比が1:2:√3→AN=3/4cm、MN=3√3/4cm
△BMNで三平方をすれば糸の長さBMが求まるが計算がやや辛い。
AN=①、MN=〇√3、AM=②とする。
AB‘=AB=④だから、BN=⑤
△BMNの辺の比で三平方をすると、BM=〇2√7
3cm=④なので、
BM=3×〇2√7/④=3√7/2cm
(2)ア あ…69.8%、い…61.2%、う…48.4%
△ABP∽△AQBの証明。

共通角より、∠BAP=∠QAB
二等辺ABCの底角より、∠ABC=∠ACB
弧ABの円周角より、∠ACB=∠APB
よって、∠APB=∠ABQ
2角相等より∽。
あ…∠ACB い…∠APB う…∠ABQ
イ 6.6%!!
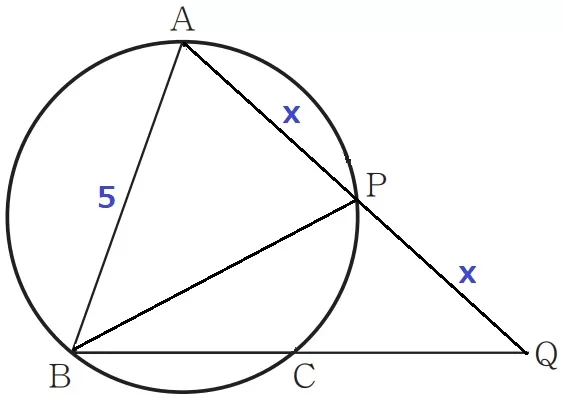
↑不要な線を消しています。
先の△ABP∽△AQBを使う。AP=xとする。
AB:AQ=AP:AB
5:2x=x:5
内項と外項の積から、2x2=25
x2=25/2
x(AP)=5√2/2cm
大問4(関数)
(1) 84.0%
y=2x2にx=-1を代入。
y=2×(-1)2=2
(2) 51.8%

同様にB座標を求める。B(2、8)
ABを斜辺とする直角三角形で三平方の定理を使う。
AB=3√5cm
(3)ア 38.8%
BCに補助線を引く。
△AOB=△AOC→等積変形でOA//BC
A→Oは右に1、下に2だから、傾きは-2。
B→Cは左に2、上に4だから、Cのy座標は8+4=12
C(0、12)
イ 1.7%!!
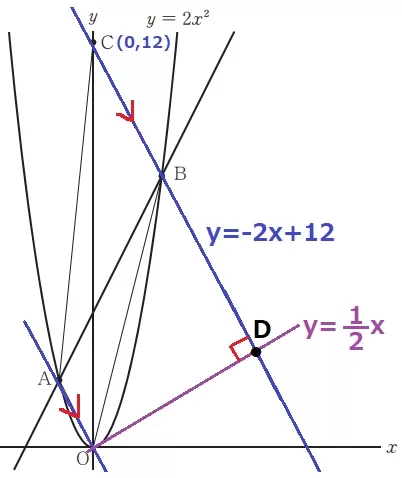
OA//BCからAとBCとの距離は、OとBCとの距離に置き換えられる。
前問より、BC;y=-2x+12
OからBCに引いた垂線の交点をDとする。
2直線の傾きの積が-1になると直交するので、OD;y=1/2x
Dのx座標を求める。
1/2x=-2x+12
x=24/5

Dから垂線をおろし、x軸との交点をEとする。
ODの傾きから、OE=②、DE=①
△ODEの辺の比で三平方をすると、求めたい距離OD=〇√5だから、
24/5×〇√5/②=12√5/5cm
大問5(文字式)
イ 29.2%!
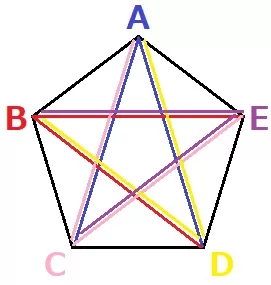
1つの頂点から対角線を引くとき、自身と両隣の3点には引けないので、
正n角形ではn-3本引ける。n個の頂点ごとに引くと全部でn(n-3)本。
しかし、2回ずつ重複してカウントするので最後に÷2をする。
正五角形の対角線は、5(5-3)/2=5本
(解答例)対角線を2回ずつ数えている
@余談@
別の対角線の数え方として、2つの頂点を選び、辺の本数を引く方法もある。
(2点を結べば直線をひける。各頂点は一直線上に3点以上並ばない。辺を除くと対角線の本数)
正六角形でいえば、6C2-6=15-6=9本
(2)ア う…64.5%、え…36.2%
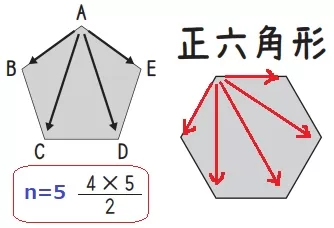
n=6のとき、5×6÷2=15本
1つの頂点から(n-1)本、頂点の数n個をかけて÷2で重複を除外する。
n(n-1)/2
う…15、え…n(n-1)
イ 31.6%!
n(n-1)/2=66
n(n-1)=132
112=121、122=144から当たりをつける。
11×12=132→n=12
12人
●講評●
大問1
配点が43点もある。
(1)オ:ルートを共通因数でくくり出す。
(4)分数があってもミスしたくない。
(5)aが分かればbも分かりやすいはずだが。
(6)対応する辺がなす角のテクは覚えておこう。
(8)イ:いわゆる不定方程式。
大問2
(2)図表の掲載がありがたい。
大問3
(1)ウ:正答率は低かったが、この系統は他県でも見られる形式。
中心角から外側に有名三角形と相場がほぼ決まっている。
(2)イ:求めたい長さに文字を置くとなんとかなる。
内項外項パターンを忘れずに!
大問4
(3)ア:2つの三角形はAOが共通辺で等積→等積変形を捉える。
イ:平行線の距離を求めればいい。原点Oで考えると計算が楽になる。
大問5
(1)イ:余力があれば、n角形の対角線の本数を求める公式を理由付きで知っておきたい。
(2)リーグ戦(総当たり戦)の試合数を図形を使って求める。
対角線の本数は自身以外。これが選手の人数分伸び、÷2で重複を回避する。




コメント