2021年度　埼玉県公立高校入試・学校選択問題【数学】解説

平均56.0点（前年比；＋0.8点）

問題はコチラ→ＰＤＦファイル
共通問題の解説はコチラ。
出題範囲の除外は円周角と中心角、三平方の定理、標本調査、実生活で相似を活用する問題。

大問１（小問集合）

（１）　88.5％
（４ｘ－ｙ）/２－（２ｘ－３ｙ）
＝（４ｘ－ｙ－４ｘ＋６ｙ）/２
＝５/２ｙ

（２）　68.1％
対称式。
ｘ＋ｙ＝（３＋√５）＋（３－√５）＝６
ｘｙ＝（３＋√５）（３－√５）＝９－５＝４

ｘ²－６ｘ＋ｙ²－６ｙ
＝ｘ²＋ｙ²－６（ｘ＋ｙ）
＝（ｘ＋ｙ）²－２ｘｙ－６（ｘ＋ｙ）
＝６²－２×４－６×６
＝－８

＠別解＠
（与式）
＝ｘ（ｘ－６）＋ｙ（ｙ－６）
＝（√５＋３）（√５－３）＋（３－√５）（－３－√５）
＝（√５＋３）（√５－３）－（３－√５）（３＋√５）
＝５－９－（９－５）
＝－４－４
＝－８

（３）　78.6％（一部正答0.3％）
（２ｘ＋１）²－７（２ｘ＋１）＝０　←（２ｘ＋１）をＸに置き換える
Ｘ²－７Ｘ
＝Ｘ（Ｘ－７）＝０
Ｘ＝０、７
２ｘ＋１＝０　→　ｘ＝－１/２
２ｘ＋１＝７　→　ｘ＝３
ｘ＝－１/２、３

（４）　93.8％
ｙの変域が０以下なので、上に凸のグラフ。
ｘ＝３のとき、最小値ｙ＝－36
ｙ＝ａｘ²は（３、－36）の点を通過するから、
－36＝３²ａ
ａ＝－４

（５）　63.2％（一部正答1.3％）
公立高校入試で有効数字はめずらしい。
整数部分が１桁だから、12700の最高位である１を１の位に置き換える。
→小数点は１と２の間にくる。
1.27×10000
10の累乗を指数を使ってあらわす。
1.27×10⁴
ア…1.27、イ…４　

（６）　88.2％
40人の中央値（メジアン）は20番目と21番目の平均。
→６～８時間の階級に含まれる。
14÷40＝0.35
0.35

（７）　89.5％
展開図でネジレ。
いろんな攻め方があると思う。

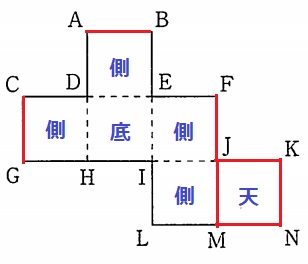
サボは面ＤＨＩＥを底面として組み立てた。
天井は面ＪＭＮＫでこの４辺と一致する辺を赤線でしるすと…
辺ＡＢ・辺ＣＧ・辺ＪＭ・辺ＫＮすべて赤くなる。
正方形の各辺なので、辺ＣＧ・ＪＭ・ＫＮは辺ＡＢと交わるか平行（ネジレではない）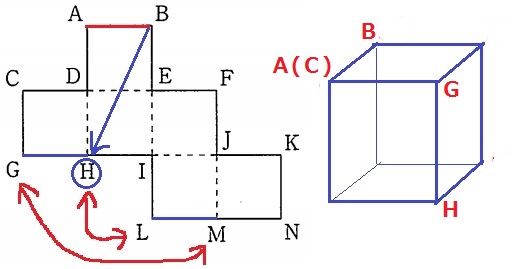
辺ＬМについて。
ＬとＨ、ＭとＧが一致するので、辺ＬＭは辺ＧＨと一致する。
展開図において、隣り合う２面からなる長方形の対角線上にある点は最も遠い点。
Ｂから最も遠い点はＨである。
ＡとＣは重なる。以上をもとに立方体をつくると、ＡＢとＧＨ（ＬМ）がネジレにある。
ウ

（８）　65.8％
方程式ではなく、算数で解きます。

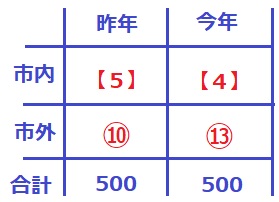
市内の生徒は、昨年：今年＝100：80＝【５】：【４】
市外の生徒は、昨年：今年＝100：130＝⑩：⑬

【５】＋⑩＝【４】＋⑬（＝500）
【１】＝③
【　】を３倍すれば〇になる。

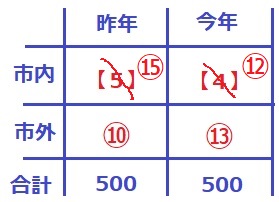
㉕＝500人
今年の市内は⑫だから、500×⑫/㉕＝240人

（９）　76.3％
赤が２連続…３/５×３/５＝９/25
白が２連続…２/５×２/５＝４/25
同色がでる確率は、９/25＋４/25＝13/25

（10）　13.5％！（一部正答12.8％、無答48.7％！）
説明問題。
図を利用する。各々の長さを求めて比べればいい。

公式解答から拝借。
端っこにある扇形を集めると１つの円になる。
アとイは直線部分で違いが出る。
差は、２ｒ×７－２ｒ×６＝２ｒｃｍ

大問２（作図・関数）

（１）　89.8％（一部正答5.6％）
作図。難しくない。

『直線ℓと直線ｍから等距離』→直線ℓ・ｍからなる角の二等分線。
『２点Ａ、Ｂから等距離』→ＡＢの垂直二等分線。
これらの交点がＰとなる。

（２）　49.7％（一部正答1.0％）

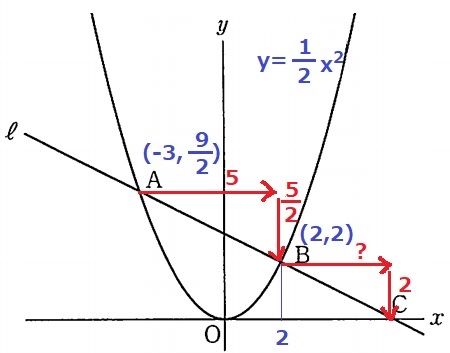
ｙ＝１/２ｘ²に代入して、Ａ（－３、９/２）Ｂ（２、２）
Ｃのｘ座標が知りたい。
Ａ→Ｂは左に５、下に５/２移動ので、傾きは１/２。
Ｂ→Ｃは下に２さがるので、左に４移動する。
Ｃのｘ座標は２＋４＝６→Ｃ（６、０）

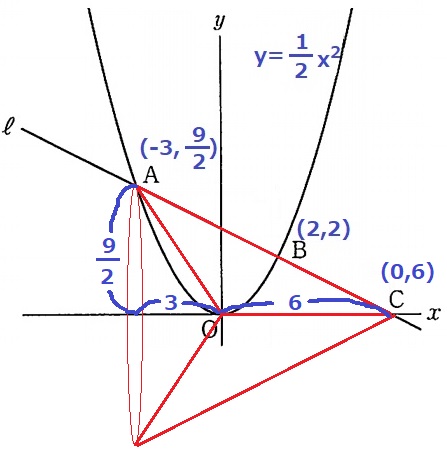
ｘ軸を軸として△ＡＯＣを回転させると、底面は半径９/２ｃｍの円、
高さ９ｃｍの円錐から高さ３ｃｍの円錐を切り取った図形になる。
⇒高さは差の６ｃｍで計算する。
９/２×９/２×π×６÷３＝81/２πｃｍ³

大問３（整数）

（１）　45.7％（一部正答16.4％）
４で割ると１余る自然数⇒４の倍数＋１⇒４ｎ＋１
（*ｎは０以上の整数。ｎ＝０、１、２、３…を代入すると、値は１、５、９、13…になる）
３ｘ＋５のｘに４ｎ＋１を代入。
３（４ｎ＋１）＋５
＝12ｎ＋８＝４（３ｎ＋２）
３ｎ＋２は整数だから、４（３ｎ＋２）は４の倍数である。
したがって、３ｘ＋５のｘに、４で割ると１余る自然数を代入すると、
３ｘ＋５の値は４の倍数になる。

（２）　41.8％（一部正答28.6％）
アで割ってイ余る自然数→アｎ＋イとしてｘに代入すると、
３（アｎ＋イ）＋５
＝３×アｎ＋３×イ＋５
＝７（〇ｎ＋△）
最終的に７の倍数になるので、７でくくれる形になるはず。
３×アｎの部分が７×〇ｎになる。
３と７は互いに素なので、アが７でないと７の倍数にならない。

今度はｎがない３×イ＋５の部分を７の倍数にする。
⇒（３の倍数＋５）が７の倍数。
表を見ると、（３の倍数＋５）＝３ｘ＋５が７の倍数となるのはｘ＝３、10…
イは１桁の整数だから３。
*ｘ＝３、10、17、24…どれも７で割ると３余る数。

（３ｘ＋５）²
＝９ｘ²＋30ｘ＋25
＝３（３ｘ²＋10ｘ＋８）＋１
↑ｘに何を入れても、３で割ると余りは１。
ア…７、イ…３、ウ…１

＠余談＠

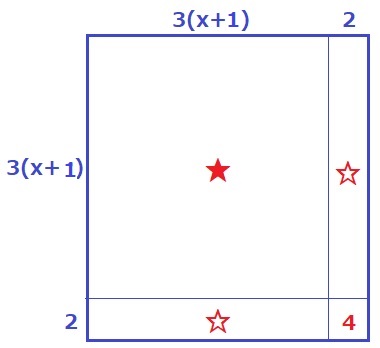
３ｘ＋５＝３（ｘ＋１）＋２
（３ｘ＋５）²を図形で表すと、１辺が３（ｘ＋１）＋２の正方形である。
★と☆は縦か横が３の倍数で３で割り切れるから、４÷３＝１…１→余りは１

大問４（平面図形）

（１）　61.2％

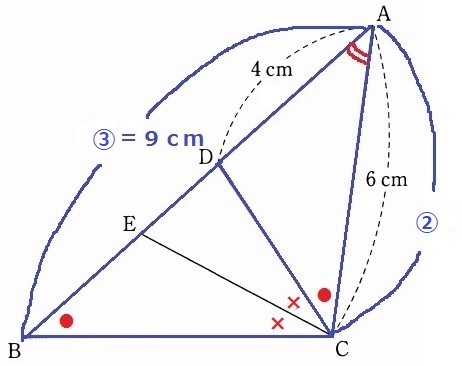
共通角で∠ＢＡＣ＝∠ＣＡＤ、∠ＡＢＣ＝∠ＡＣＤより、
２角が等しく、△ＡＢＣ∽△ＡＣＤ
ＡＢ：ＡＣ＝ＡＣ：ＡＤ＝６：４＝③：②
ＡＢ＝６×③/②＝９ｃｍ

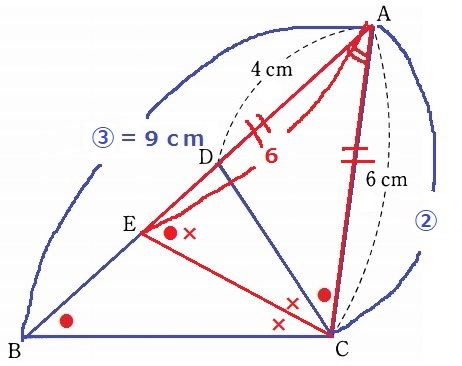
△ＢＣＥで外角定理→∠ＡＥＣ＝●×
△ＡＥＣの底角が●×で等しく、二等辺三角形とわかる。
ＡＥ＝６ｃｍ
ＢＥ＝９－６＝３ｃｍ

（２）　11.8％！（一部正答64.1％）
△ＡＤＨ∽△ＡＣＦの証明。

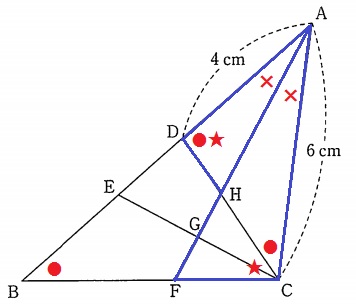
∠ＢＡＣの二等分線から、∠ＤＡＨ＝∠ＣＡＦ（×）
仮定から、∠ＤＢＣ＝∠ＡＣＤ（●）
△ＢＣＤで外角定理→∠ＡＤＨ＝●＋★
∠ＡＣＦ＝●＋★
∠ＡＤＨ＝∠ＡＣＦ
２角が等しく∽。

（３）　7.6％!!（無答47.4％）

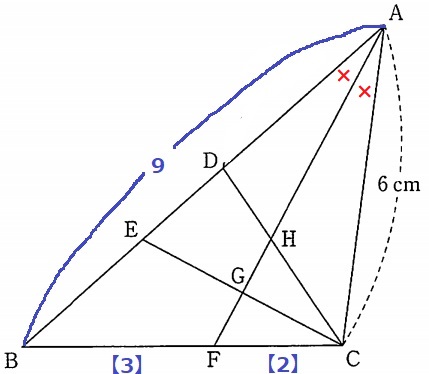
角の二等分線の定理から、ＡＢ：ＡＣ＝ＢＦ：ＦＣ＝３：２
△ＡＦＣの面積は△ＡＢＣの２/５。

前問の△ＡＤＨ∽△ＡＣＦの相似比より、ＤＨ：ＣＦ＝②：③
角の二等分線の定理から、ＡＤ：ＡＣ＝ＤＨ：ＨＣ＝②：③
ＤＨがともに②なので、比をそのまま統一できる。
△ＣＦＨは等辺③の二等辺三角形。

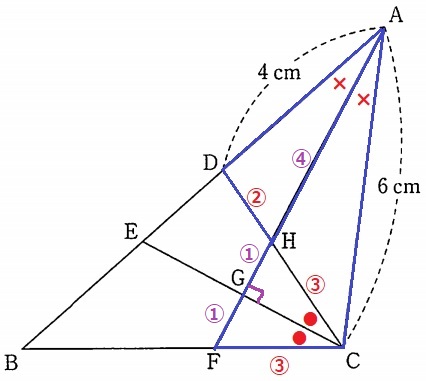
二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。
ＨＧ＝ＧＦ＝①とする。
△ＡＤＨ∽△ＡＣＦの相似比からＡＨ：ＡＦ＝２：３だから、
この比の差である１がＨＦ＝②に相当するので、ＡＨ＝④
【△ＡＢＣ→△ＡＦＣ→△ＧＦＣ】
18×２/５×①/⑥＝６/５ｃｍ²

＠別解＠

角の二等分線より、ＡＢ：ＡＣ＝ＢＦ：ＦＣ＝③：②
（１）より、△ＡＥＣは二等辺三角形。
二等辺の頂角の二等分線は底辺ＥＣを垂直に二等分する。
ＥＧ＝ＧＣ
【△ＡＢＣ⇒△ＥＢＣ⇒△ＧＢＣ⇒△ＧＦＣ】
18×３/９×１/２×②/⑤＝６/５ｃｍ²
*学校選択では（２）で△ＡＤＨ∽△ＡＣＦの証明が課されていますが、
この誘導を無視して、△ＣＦＨではなく△ＡＥＣの二等辺三角形を使ってもＯＫです。
むしろ、共通問題のように解いたほうがサボはやりやすかったです。

＠別解２＠

ＥＧ＝ＧＣより、△ＡＢＧと四角形ＡＧＢＣは９ｃｍ²

ＡＥ：ＥＢ＝２：１から、△ＡＧＣ：△ＢＧＣ＝２：１
△ＡＧＣ＝６ｃｍ²、△ＢＧＣ＝３ｃｍ²

△ＡＢＧ：△ＡＣＧ＝３：２より、ＢＦ：ＦＣ＝③：②
△ＧＦＣ…３×②/⑤＝６/５ｃｍ²
中学受験の世界では『ベンツ切り』というそうな( ´д)ﾋｿ(´д｀)ﾋｿ(д｀ )

大問５（数量変化）

（１）　73.4％（一部正答17.1％）
０≦ｘ≦４において、△ＡＰＱは直角二等辺三角形。
底辺ＡＰと高さＡＱはともにｘｃｍ。
ｙ＝ｘ×ｘ÷２＝１/２ｘ²
ｙ＝１/２ｘ²

（２）　1.6％!!（一部正答5.9％、無答47.0％）
転換点に気を付けて調べていきます。
◆０≦ｘ≦４のとき

△ＡＰＱ…底辺ｘｃｍ、高さｘｃｍ
△ＡＱＣ…底辺ｘｃｍ、高さ２ｃｍ
底辺がともにｘｃｍ→△ＡＰＱ：△ＡＱＣ＝３：１となるには高さが３：１になればいい。
ＡＰ＝２×３＝６
しかし、０≦ｘ≦４だから条件不適合×。

◆４≦ｘ≦５のとき

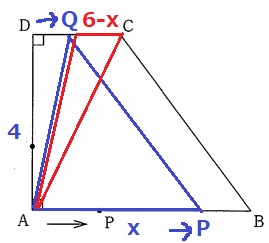
△ＡＰＱ…底辺ｘｃｍ、高さ４ｃｍ
△ＡＱＣ…底辺ＱＣはＡ～ＣからＡ～Ｑを引く→６－ｘｃｍ、高さは４ｃｍ。
高さがともに４ｃｍ→△ＡＰＱ：△ＡＱＣ＝３：１となるには底辺が３：１になればいい。
ｘ＝３（６－ｘ）
ｘ＝９/２
４≦ｘ≦５だから条件適合〇。

◆５≦ｘ≦６のとき
△ＡＱＣはさらに減少して、ｘ＝６のときに面積が０ｃｍ²になる。
△ＡＰＱはさらに増加する。条件不適合×。

◆６≦ｘ≦11のとき

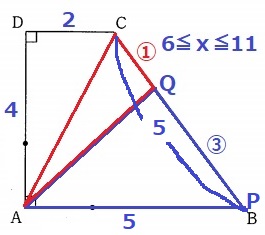
△ＡＰＱ：△ＡＱＣ＝３：１となるとき→ＣＱ：ＱＢ＝１：３
ｘ＝４＋２＋５×①/④＝29/４
したがって、ｘ＝９/２、29/４

（３）　2.0％!!（一部正答23.0％、無答61.5％）
台形ＡＢＣＤの面積の半分は、（２＋５）×４÷２÷２＝７ｃｍ²

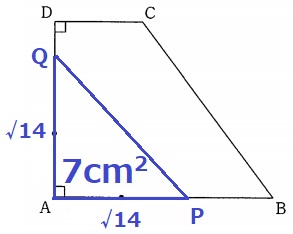
ｘ＝４のとき、△ＡＰＱの面積は４×４÷２＝８ｃｍ²だから、
１つ目は０≦ｘ≦４のとき。
△ＡＰＱは直角二等辺三角形なので、１/２ｘ²＝７
ｘ＝√14

その後、△ＡＰＱの面積は増加し、ＱがＣＰを移動しているときに減少する。
△ＡＣＤ＝４×２÷２＝４ｃｍ²
△ＡＣＱ＝７－４＝３ｃｍ²
ＣＱ：ＱＰ＝△ＡＣＱ：△ＡＰＱ＝③：⑦
ｘ＝４＋２＋５×③/⑩＝15/12
したがって、ｘ＝√14、15/２