2023年度　新潟県公立高校入試問題過去問【数学】解説

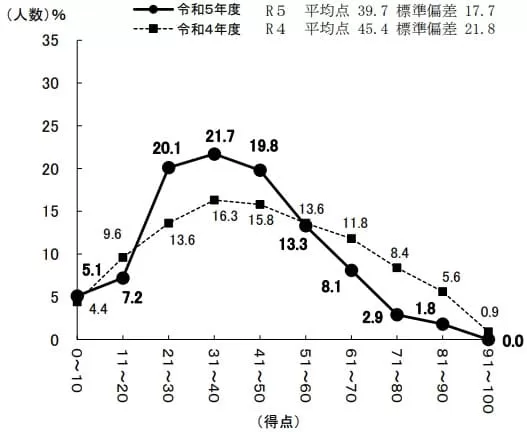
平均39.7点（前年比；－5.7点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－73.7％

（１）　92.2％
７－（－３）－３
＝７＋３－３
＝７

（２）　92.4％
２（３ａ－２ｂ）－４（２ａ－３ｂ）
＝６ａ－４ｂ－８ａ＋12ｂ
＝－２ａ＋８ｂ

（３）　85.9％
（－６ａｂ）²÷４ａｂ²
＝36ａ²ｂ²÷４ａｂ²
＝９ａ

（４）　86.8％
ｘ＋３ｙ＝21　…①
２ｘ－ｙ＝７　…②
①×２－②をすると、７ｙ＝35
ｙ＝５
①に代入すると、ｘ＝６
ｘ＝６、ｙ＝５

（５）　85.5％
√45－√５＋10/√５
＝３√５－√５＋２√５
＝４√５

（６）　62.3％
支払金額…130ａ円
代金の合計…５ｂ＋150×５＝５ｂ＋750円
おつりがあった→130ａ円の方が高い。
130ａ＞５ｂ＋750

（７）　38.5％

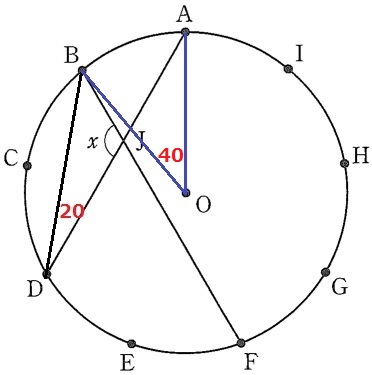
各点は円周を９等分する→∠ＡＯＢ＝360÷９＝40°
円周角は中心角の半分だから、弧ＡＢに対する円周角ＡＢＤ＝40÷２＝20°
 
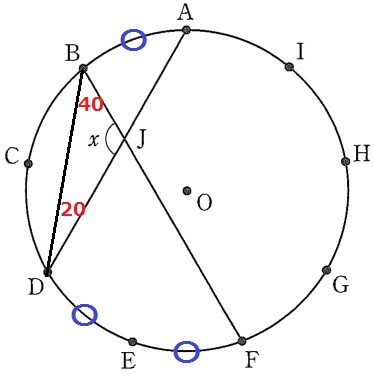
弧ＤＦは弧ＡＢの２倍の長さ→円周角も２倍→∠ＤＢＦ＝20×２＝40°
△ＢＤＪの内角より、ｘ＝180－（20＋40）＝120°

（８）　46.0％
最小値：52～54ｇ
最大値：62～64ｇ
40個の中央値は20番目と21番目の平均。
いずれも58～60ｇの階級に属する→イ除外

第１四分位数は下位20個の真ん中、下から10番目と11番目の平均。
56～58ｇの階級に属する→エ除外
第３四分位数は上位10個の真ん中、上から10番目と11番目の平均。
58～60ｇの階級に属する→ウ除外
よって、ア。

大問２（小問集合２）―39.2％

（１）　56.3％
答案では求める過程も記述する。
全体は、６×６＝36通り
24/（ａ＋ｂ）が整数になる→ａ＋ｂは24の約数。
２つのサイコロの出目の和より、２≦ａ＋ｂ≦12
この範囲にある24の約数で場合分けする。
●２→１通り
●３→２通り
●４→３通り
●６→５通り
●８→５通り
●12→１通り
計17通りだから、確率は17/36。

（２）　41.9％
ＡＢ＝ＥＣの証明。

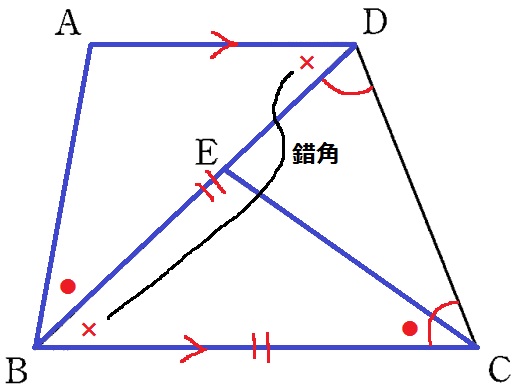
これらが対応する辺となる△ＡＢＤ≡△ＥＣＢを証明すればいい。
仮定より、∠ＤＢＡ＝∠ＢＣＥ（●）
∠ＢＣＤ＝∠ＢＤＣより、△ＢＣＤは二等辺三角形だからＢＤ＝ＣＢ
ＡＤ//ＢＣの錯角で、∠ＡＤＢ＝∠ＥＢＣ
１辺と両端角と等しいから、△ＡＢＤ≡△ＥＣＢ
対応する辺は等しいので、ＡＢ＝ＥＣ

（３）　19.4％！

直線ℓとｍに接し、かつＡを通る円の中心を作図する。
Ａを通る対称の軸と線対称をイメージしよう！
円の中心Ｏ、Ｏ’は２直線とＡから半径の長さ分、離れている。
ＯとＯ’は左右対称の位置関係で、直線ℓとｍの真ん中にある。

位置が固定されているのはＡなので、Ａから出発する。
①対称の軸は、Ａを通る直線ℓ、ｍに対する垂線。
②円の中心は２直線の真ん中→２つの★の垂直二等分線上にある。
③円の中心は対称関係にある→対称の軸上にあるＡから等距離（半径）。
円の半径は●と★の距離で、この長さをとってＡから移す。

大問３（数量変化）―28.0％

（１）　51.8％

Ｐの速さは毎秒２ｃｍである点に注意！
ｘ＝２、つまり２秒後にＰは４ｃｍ移動している。
このとき、正方形ＰＱＲＳは長方形ＯＡＢＣの内部にある。
ｙ＝４²＝16

（２）①　27.7％！

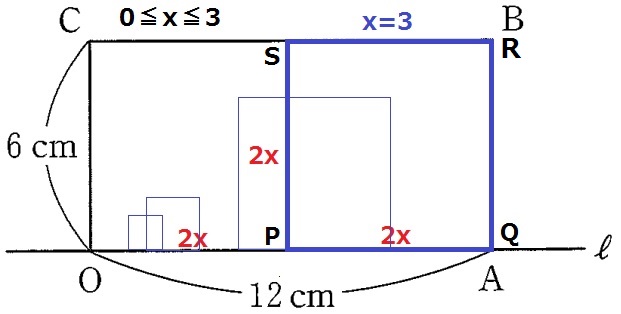
ｘ＝３のときを考える。ＯＰ＝２×３＝６ｃｍ
すなわち、ＰはＯＡの中点でＱはＡにいる。
０≦ｘ≦３のとき、正方形ＰＱＲＳは長方形ＯＡＢＣの中に収まる。
正方形の１辺の長さはＰが動いた距離である２ｘだから、
ｙ＝（２ｘ）²＝４ｘ²

②　21.6％！

ｘ＝３を過ぎてから正方形が長方形をはみ出していき、ｘ＝６で完全にはみ出す。

赤い正方形ＰＱＲＳに着目して、重なっている面積を求める。
重なり部分の縦は６ｃｍ、横は12－２ｘｃｍ。
３≦ｘ≦６のとき、ｙ＝６（12－２ｘ）＝－12ｘ＋72

＠別解＠
ｘ＝３のとき、ｙ＝６×６＝36
そこから徐々に重なり部分が減少する。
縦は６ｃｍのままで横だけが短くなるから、面積は一次関数で減少し、
ｘ＝６のときにｙ＝０となる。
（３、36）と（６、０）を通る直線の式を求めると、ｙ＝－12ｘ＋72

（３）　21.6％！

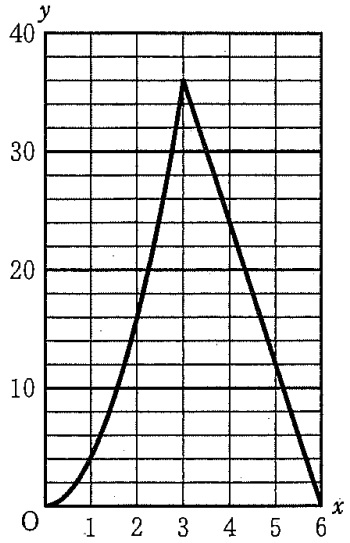
前問より、０≦ｘ≦３のとき、ｙ＝４ｘ²
ｙ＝ａｘ²の形だから放物線で増加、ｘ＝３のときｙ＝36
３≦ｘ≦６のとき、ｙ＝－12ｘ＋72
一次関数で減少し、ｘ＝６のときｙ＝０

（４）　28.5％！
答案では求める過程も記述する。

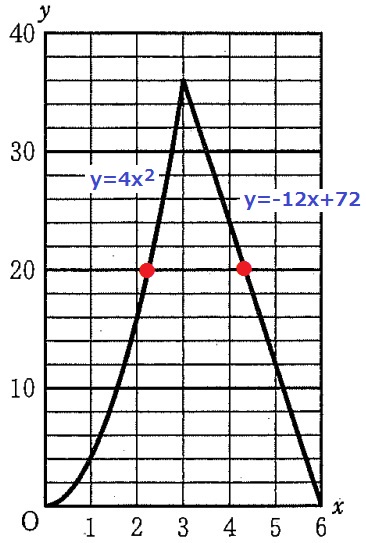
式はわかっているので、これにｙ＝20を代入すればいい。
０≦ｘ≦３のとき、20＝４ｘ²
ｘ＝√５（≒2.2360679…：富士山麓オウム鳴く）条件適合

３≦ｘ≦６のとき、20＝－12ｘ＋72
ｘ＝13/３　条件適合
ｘ＝√５、13/３

大問４（整数）―14.2％

（１）ア…17.3％！、イ…36.7％、ウ…34.0％
箱からカードを取り出すのは最初の２回だけ。
手順Ⅲ：（ｎ－２）番目と（ｎ－１）番目の和を求め、その一の位の数をｎ番目に記入する。
⇒ようは２個前と１個前の和の一の位を記入していく。

３番目は２＋３＝５、４番目は３＋５＝８、５番目は５＋８＝13→３
６番目は８＋３＝11→１、７番目は３＋１＝４、８番目は１＋４＝５
９番目は４＋５＝９、10番目は５＋９＝14→４、11番目は９＋４＝13→３
12番目は４＋３＝７、13番目は３＋７＝10→０、14番目は７＋０＝７長い…
15番目０＋７＝７、16番目７＋７＝14→４、17番目７＋４＝11→１、18番目４＋１＝５
ア…４、イ…１、ウ…５

（２）①　0.3％!!!
難しい(;°;ω;°;)というか、問題が良くない。

↑公式解答より。
１番目をａ、２番目をｂとして、ひたすら足している。
必要なのは１の位なので、十の位以上を除外している。除外しないで書くと以下のようになる。
①ａ、②ｂ、③ａ＋ｂ、④ｂ＋（ａ＋ｂ）＝ａ＋２ｂ、⑤（ａ＋ｂ）＋（ａ＋２ｂ）＝２ａ＋３ｂ
⑥（ａ＋２ｂ）＋（２ａ＋３ｂ）＝３ａ＋５ｂ、⑦（２ａ＋３ｂ）＋（３ａ＋５ｂ）＝５ａ＋８ｂ…
⑧８ａ＋13ｂ、⑨13ａ＋21ｂ、⑩21ａ＋44ｂ、⑪44ａ＋65ｂ、⑫65ａ＋109ｂ、⑬109ａ＋174ｂ
⑭174ａ＋283ｂ、⑮283ａ＋457ｂ、⑯457ａ＋740ｂ、⑰740ａ＋1217ｂ
⑰の十の位以上を除外すると７ｂとなる。
つまり、２番目の数を７倍した数の一の位が17番目の数に相当する。
なんでこんなの出したんだ(`д´)

②　2.1％!!
答案では求める過程も記述する。

前問より、16番目は７ｘの一の位。17番目は７×４＝28→８。
７ｘの一の位と８を足した数の一の位が18番目の１となる。

一の位が８から１に変わるということは、８＋３＝11→１
なぜなら、一の位は最大で９、８＋□が21以上になることはないから。
７ｘの一の位が３、言い換えれば、７の段で一の位が３なのは７×９＝63しかない。
ｘ＝９

大問５（空間図形）―10.9％

（１）　25.4％！

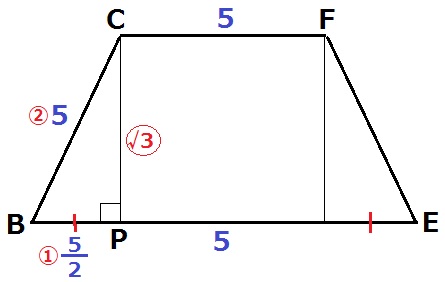
四角形ＣＢＥＦは等脚台形で左右対称。
ＢＰ＝（10－５）÷２＝５/２ｃｍ
△ＣＢＰの辺の比で三平方。
ＣＢ：ＢＰ＝②：①だから、三平方よりＣＰ＝〇√３
ＣＰ＝５/２×〇√３＝５√３/２ｃｍ

（２）　7.2％!!
答案では求める過程も記述する。

四角錘の底面積は５×10＝50ｃｍ²、高さがわかればいい。
Ｃから垂線をひき、ＡＤとの交点をＱ、面ＡＢＥＤとの交点をＨする。
△ＣＱＰは等辺が５√３/２ｃｍの二等辺三角形で、ＨはＱＰの中点である。
ＨＰ＝５÷２＝５/２ｃｍ

△ＣＨＰの辺の比で三平方をすると、①：〇√２：〇√３。
立体の高さＣＨ＝５/２×〇√２＝５√２/２ｃｍ
四角錘ＣーＡＢＥＤの体積は、50×５√２/２÷３＝125√２/３ｃｍ³

（３）　0.9％!!!
答案では求める過程も記述する。

↑公式解答より。やけにスッキリしている。。(･Д･)

立体Ｃ―ＡＢＦを面ＣＮＦで分割すると、
立体Ｃ―ＡＢＦ＝三角錘ＡーＣＮＦ＋三角錘Ｂ―ＣＮＦ

△ＡＢＣは正三角形、Ｎは底辺ＡＢの中点→ＡＢ⊥ＣＮ
△ＣＮＦを底面としたとき、高さの合計がＡＢ（５ｃｍ）の三角錐を求めれば良い。
５×５√２/２÷２×５÷３＝125√２/12ｃｍ³