2022年度　山口県公立高校入試問題過去問【数学】解説

平均24.5点（前年比；－1.2点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
８－（－５）
＝８＋５
＝13

（２）
２/５÷（－１/10）
＝２/５×（－10）
＝－４

（３）
（－４ａ）²×３ｂ
＝16ａ²×３ｂ
＝48ａ²ｂ

（４）
（６ｘ＋ｙ）－（９ｘ＋７ｙ）
＝６ｘ＋ｙ－９ｘ－７ｙ
＝－３ｘ－６ｙ

（５）
（ａ＋３）（ａ－３）
＝ａ²－９

大問２（小問集合）

（１）
水面の高さは最初（０分後）が７ｃｍ。ｘ分後には３ｘｃｍ増加する。
ｙ＝３ｘ＋７

（２）
19個の中央値（メジアン）は、（19＋１）÷２＝10番目の値。
これは200～300人の階級に含まれる。
イ

（３）
①【４より大きく５より小さい無理数】
４＝√16、５＝√25だから、該当する範囲は√17～√24。
②【２乗すると18より小さい整数となる】
√18より小さい。
したがって√17

（４）

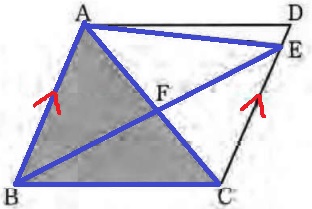
ＡＢ//ＤＣで等積変形。
△ＡＢＣと△ＡＢＥが等積である。
ウ

大問３（方程式）

（１）
静止画の合計が３ａＭＢ、動画の合計が80ｂＭＢ。
これらの和が500よりも小さかった。
３ａ＋80ｂ＜500

（２）
Ｓの結果で等式。
20ｘ＋10ｙ＝198　…①
Ｔの結果で等式。
５ｘ＋30ｙ＝66　…②

②×４－①をすると、110ｙ＝66
ｙ＝0.6
②に代入して、ｘ＝9.6
アプリＰ…9.6ＭＢ、アプリＱ…0.6ＭＢ

大問４（空間図形）

（１）
回転体は半径３ｃｍの球である。
球の体積Ｖ＝４/３πｒ³
４/３π×３³
＝36πｃｍ³

（２）

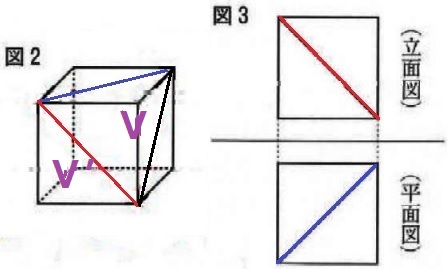
立面図は正面から、平面図は真上からみた図。
対応する線分に意識すると、切り取る立体は上図の三角錐である。
手前がＶで奥がＶ’。

三角錐Ｖ＝①としてさかのぼると、四角錘は高さが同じで底面積が２倍だから②。
〔錘⇒柱〕は３倍なので立方体の体積は⑥。残りのＶ’は⑤。
よって、Ｖ：Ｖ’＝１：５
ウ

大問５（規則）

（１）
買ってきた花の数は、５×70＝350個
ａ人が同じ数ずつ植えると、１人あたり350÷ａ＝350/ａ個植える。
*反比例

（２）
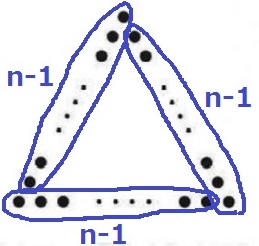
Ｂの考え方である３（ｎ－２）＋３の意味を図を用いて説明する。

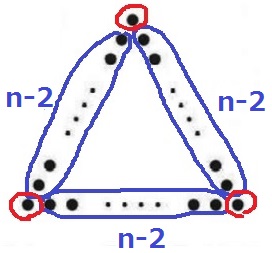
３（ｎ－２）の３は正三角形の辺の数。
正三角形の１辺のどこが（ｎ－２）にあたるか。
－２ということは両端を弾いている。
つまり、正三角形の１辺ｎの両端を除外したｎ－２を３つ掛け合わせ、
最後に頂点３つを足した。

＠余談＠

一番やりやすいのはこれです。

大問６（データの活用・確率）

（１）
ア：四分位範囲＝Ｑ3（第３四分位数）－Ｑ1（第１四分位数）
10回を前半と後半の５回ずつに分け、おのおのの真ん中がＱ3とＱ1である。
Ｑ3は上から３番目（下から７番目）で９。Ｑ1は下から３番目で６。
四分位範囲は、９－６＝３

イ：同様に、Ｂの四分位範囲を求める。
前半と後半の25回ずつの真ん中は、Ｑ3が上から13番目の９、Ｑ1が下から13番目の４。
Ｂの四分位範囲は、９－４＝５
四分位範囲が大きいＢの方が散らばりの度合いが大きい。
ア…３、イ…Ｂ

＠大数の法則＠
試行回数を増やしていくほど、ある事象が発生する割合が一定の値に近づいていく。
サイコロのある出目は、６回より6000回投げた方が確率１/６に近づく。

（２）
答案では過程も記述する。
和が６以上８以下を書き出すしかない。
●和が６…（１、５）（２、４）（３、３）（４、２）（５、１）
●和が７…（１、６）（２、５）（３、４）（４、３）（５、２）（６、１）
●和が８…（２、６）（３、５）（４、４）（５、３）（６、２）
計16通り
全体は６×６＝36通りだから、確率は16/36＝４/９

大問７（関数）

（１）
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ＝１なので、１（－３－１）＝－４

（２）

ｘの値を各グラフに代入して、Ａ（２、４）Ｂ（－３、９ａ）
ａの値を求めるには、ｙ＝ａｘ²上にあるＢ座標が必要である。
△ＯＡＢは面積８、幅５だから、高さは８×２÷５＝16/５
→ＡＢの切片は16/５である。
 
赤線の直角三角形は相似で、相似比は②：③。
Ａのｙ座標と切片の差は、４－16/５＝４/５
切片とＢのｙ座標の差は、４/５×③/②＝６/５
Ｂのｙ座標は、16/５－６/５＝２
９ａ＝２
ａ＝２/９

大問８（平面図形）

（１）

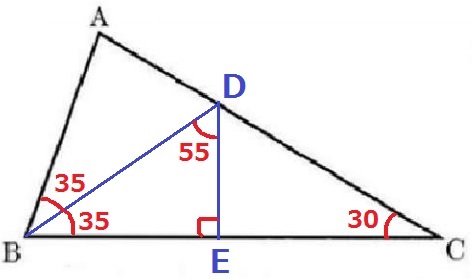
角度の情報が多いので、適当なＤとＥを描いて方針をさぐる。
△ＤＢＥの内角から、∠ＤＢＥ＝180－（90＋55）＝35°
ＢＤは∠ＡＢＣの二等分線である。

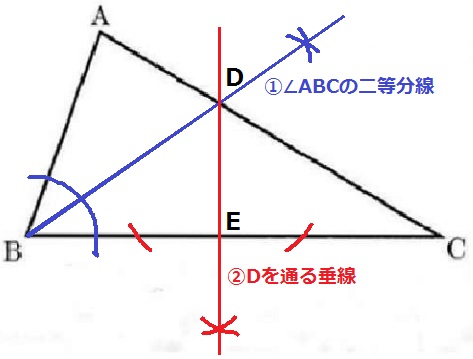
①∠ＡＢＣの二等分線。ＡＣとの交点がＤ。
②Ｄを通るＢＣの垂線を作図。交点がＥとなる。

（２）
ＢＡ：ＢＣ＝ＡＰ：ＣＰの証明。
対応する辺の相似を使う。ＣＰ＝ＣＱからＣＰをＣＱに置き換えてみる。

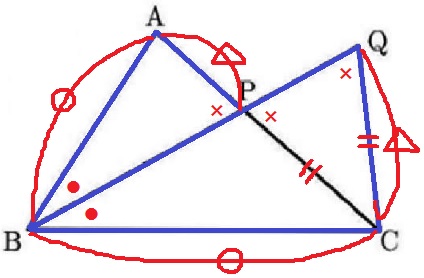
△ＡＢＰと△ＣＢＱに着目。
仮定（∠ＡＢＣの二等分線）から∠ＡＢＰ＝∠ＣＢＱ（●）
△ＰＣＱは二等辺三角形。底角を×とすると、対頂角で∠ＱＰＣ＝∠ＡＰＢ（×）
２角が等しいから、△ＡＢＰ∽△ＣＢＱ
対応する辺の比で、ＢＡ：ＢＣ＝ＡＰ：ＣＱ
ＣＰ＝ＣＱより、ＢＡ：ＢＣ＝ＡＰ：ＣＰ

＠別解＠

角の二等分線の定理を知っている人は、
『仮定の二等分線から角の二等分線の定理よりＢＡ：ＢＣ＝ＡＰ：ＣＰ』で良いと思う。

大問９（総合問題）

（１）
無作為に抽出した20個のうち、使える玉は15個だった。
⇒使える玉の割合は、15/20＝３/４
413×３/４＝309.7…≒310個

（２）

接点で半径を結ぶと直線になる。
小さい円の半径がｘｍ。どこかで三平方を使って方程式を立てる。
長方形の縦18ｍと横22ｍから両端のｘを引いた18－２ｘｍ、22－２ｘｍ、
斜辺を14＋２ｘｍとする直角三角形が見つかるが計算がしち面倒くさい(´Д｀)

中心Ｏに着目して、うえのように各辺を半分にすることができる。
（11－ｘ）²＋（９－ｘ）²＝（ｘ＋７）²
121－22ｘ＋ｘ²＋81－18ｘ＋ｘ²＝ｘ²＋14ｘ＋49
ｘ²－54ｘ＋153
＝（ｘ－３）（ｘ－51）＝０
小さい円は円Ｏより小さい。ｘ＜７より、ｘ＝３

（３）ア
答案では求める過程も記述する。

第１レーンも第４レーンも直線部分は同じ。差がつくのは曲線部分である。
曲線部分は内側の弧の長さを測る。第１レーンの半径はｒｍ、第４レーンの半径はｒ＋３ｍ。
赤線の弧と青線の弧の差が求めたい長さに相当する。
２π（ｒ＋３）－２πｒ＝６πｍ

イ
Ｂがある第４レーンだけを見る。

半径は、ｒ＋３＝21＋３＝24ｍ
半円の弧の長さは、24×２×π÷２＝24πｍ
中心角は弧の長さに比例するので、∠ＢＡＣ＝180°×６/24＝45°