2020年度　宮崎県公立高校入試問題過去問【数学】解説

合格者平均53.9点（前年比；＋3.4点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－82.2％

（１）　97.9％
－９＋（－８）
＝－17

（２）　91.3％
３/４÷（－５/６）
＝－９/10

（３）　90.0％
２（ａ＋４ｂ）－（－３ａ＋７ｂ）
＝２ａ＋８ｂ＋３ａ－７ｂ
＝５ａ＋ｂ

（４）　83.4％
√12×√２÷√６　←根号のまま約分
＝２

（５）　84.8％
２ｘ＋３ｙ＝20　…①
４ｙ＝ｘ＋１　…②

②より、ｘ＝４ｙ－１
①に代入。２（４ｙ－１）＋３ｙ＝20
11ｙ＝22
ｙ＝２

②に代入して、４×２＝ｘ＋１
ｘ＝７
ｘ＝７、ｙ＝２

（６）　71.7％
３ｘ²－ｘ－１＝０
因数分解ができないので解の公式。
ｘ＝（１±√13）/６

（７）　66.3％
和が８にならないよりなる場合のほうが少ない。
和が８→（２、６）（３、５）（４、４）（５、３）（６、２）
以上、５通り。
全体が６×６＝36通りで、和が８にならないのは36－５＝31通り
確率は、31/36。

（８）　72.0％

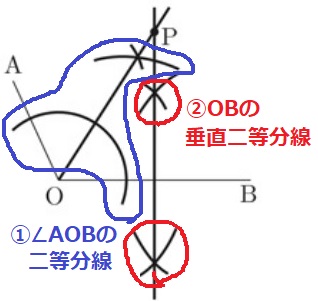
①∠ＡＯＢに二等分線
②ＯＢの垂直二等分線
これらの交点がＰとなる。

大問２（データの活用・規則）－58.4％

（１）①　98.4％
40－（４＋７＋11＋６＋２）
＝10

②　48.1％
完全解答。
ア：16冊以上はともに８人で等しい。〇
イ：最頻値（モード）は１年が14冊、２年が14冊で等しい。×
ウ：最大値の含まれる階級は20～24冊で等しい。〇
エ：30人の中央値（メジアン）は15番目と16番目の平均で14冊。
40人の中央値は20番目と21番目の平均で10冊。１年の方が大きい×
ア・ウ

③　57.6％
答案では説明を記述する。
相対度数を算出して比較すればいい。
１年生…10÷30＝0.333…≒0.33
２年生…11÷40＝0.275≒0.28
0.33＞0.28だから、12冊以上16冊未満の生徒の割合が大きいのは１年生。

（２）①　56.7％

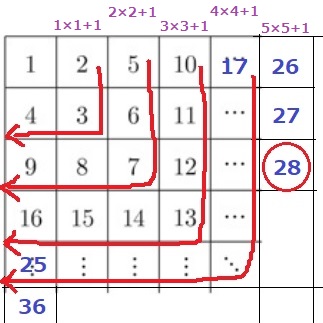
１行目の〔１、２、５、10、17、26…〕は
最初の１を除き、ｎ列目の〔ｎ－１の平方数＋１〕
１行目６列目は５×５＋１＝26
３行目６列目は26＋２＝28
１―28
*（３、６）と（６、３）を取り違えないように！
横行→縦列の順です。

右列は平方数が並ぶ。
31行目１列目は、31×31＝961
２—961

②　32.9％！

これも平方数から攻めた方がやりやすいと思う。
１²－０＝１
２²－１＝３
３²－２＝７
４²－３＝13
…ｎ²－（ｎ－１）
＝ｎ²－ｎ＋１

大問３（数量変化）－46.7％

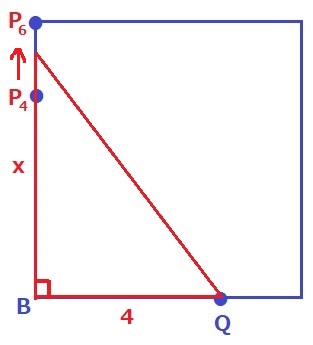
（１）　72.4％
△ＰＢＱは等辺が１ｃｍの直角三角形。
ｙ＝１×１÷２＝１/２

（２）　49.8％
４秒後までは底辺ＢＱと高さＰＢが１ｃｍずつ長くなる。
底辺と高さがともに伸びるので、ｙ＝ａｘ²で増えていく。
ｘ＝２のとき、ｙ＝２×２÷２＝２
ウ

（３）　43.5％
転換点に注意を払う。

４秒後～６秒後は高さＰＢが伸びる。
ｙ＝４×ｘ÷２＝２ｘ
①…６、②…２ｘ

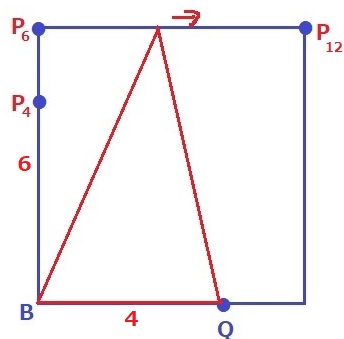
６秒後から12秒後までは等積変形で面積が一定。
ｙ＝４×６÷２＝12
③…12、④…12

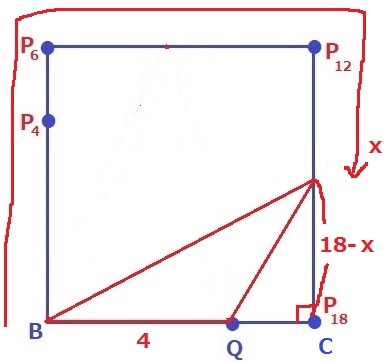
12秒後～18秒後の高さは、ＢからＣまでの距離18ｃｍから、
Ｐの移動距離ｘｃｍを引いて18－ｘｃｍ。
ｙ＝４×（18－ｘ）÷２＝－２ｘ＋36
⑤…－２ｘ＋36

（４）　21.9％！
ｙ＝６×６÷８＝９/２となるｘの値を求める。
ｘ＝４のとき、ｙ＝４×４÷２＝８だから、１つは０≦ｘ≦４

ｙ＝ａｘ²に（ｘ、ｙ）＝（４、８）を代入してａ＝１/２
ｙ＝１/２ｘ²
ｙ＝９/２を代入。
１/２ｘ²＝９/２
ｘ＞０、ｘ＝３

ｘ＝12のときｙ＝12だから、もう１つは12≦ｙ≦18
ｙ＝－２ｘ＋36にｙ＝９/２を代入して、ｘ＝63/４
ｘ＝３、63/４

大問４（平面図形）－38.0％

（１）　62.9％

半円の弧に対する円周角で、∠ＡＢＣ＝90°
∠ＥＢＣ＝90－24＝66°
△ＢＣＥで外角定理→∠ＡＣＢ＝100－66＝34°

（２）　51.4％
△ＦＢＤ∽△ＦＣＡの証明。

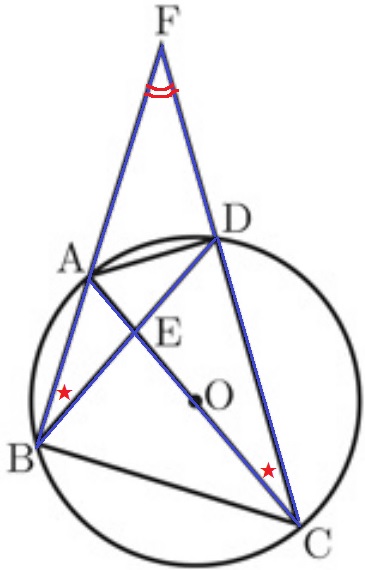
共通角で∠ＢＦＤ＝∠ＣＦＡ
弧ＡＤに対する円周角で∠ＦＢＤ＝∠ＦＣＡ
２角が等しく∽。

（３）　33.2％！
前問の相似を用いる。

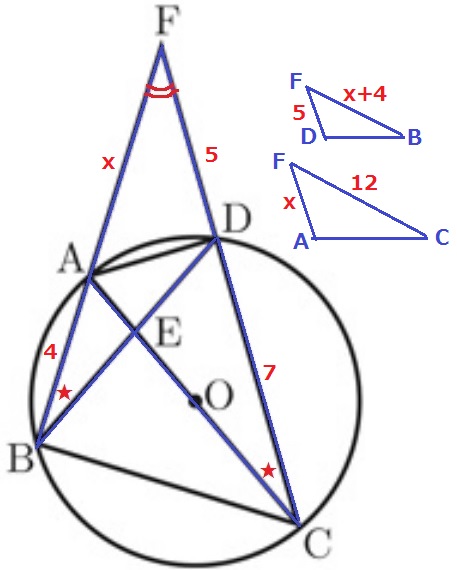
対応する辺がごちゃごちゃになったら、三角形を描いて整理してみよう。
ＦＤ：ＦＢ＝ＦＡ：ＦＣ
５：ｘ＋４＝ｘ：12
内項と外項の積より、ｘ（ｘ＋４）＝60
ｘ²＋４ｘ－60
＝（ｘ＋10）（ｘ－６）＝０
ｘ＞０、ｘ＝６
ＡＦの長さは６ｃｍ。

（４）　1.1％!!

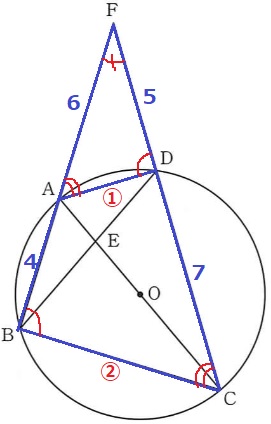
内接四角形の内角は、その対角の外角に等しい。
∠ＦＡＤ＝∠ＦＣＢ、∠ＦＤＡ＝∠ＦＢＣ
２角相等で△ＦＡＤ∽△ＦＣＢ。
ＡＤ：ＣＢ＝ＦＡ：ＦＣ＝６：12＝①：②

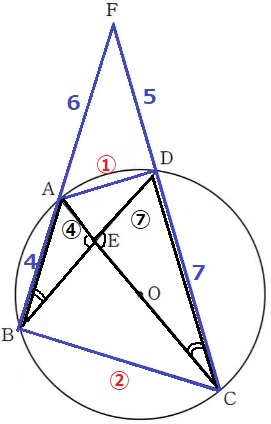
対頂角と円周角で△ＡＢＥ∽△ＤＣＥ。
対応する辺を誤らないように！
ＡＥ：ＤＥ＝ＡＢ：ＤＣ＝④：⑦

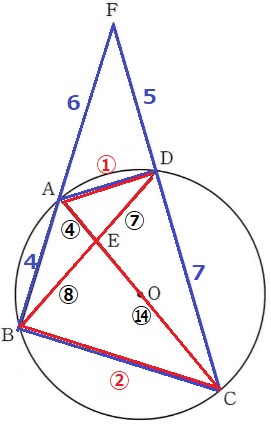
同様に、△ＡＤＥ∽ＢＣＥ。
△ＡＤＥと△ＢＣＥの辺の比は、ＡＤ：ＢＣ＝①：②
ということは、ＥＣ＝ＥＤ×２＝⑭

ＦＤ：ＤＣ＝５：７
△ＡＤＦの面積を【５】とおくと、△ＡＤＣの面積は【７】
ＡＥ：ＥＣ＝④：⑭＝２：７より、△ＡＤＥの面積は【７】×２/９＝【14/９】
△ＡＤＥ：△ＡＤＦ＝【５】：【14/９】＝45：14
△ＡＤＥは△ＡＤＦの14/45倍。

大問５（空間図形）－30.1％

（１）　85.2％
ネジレ→延長しても交わらない、かつ平行でない。
辺ＡＤとネジレにある辺は、辺ＢＦ、辺ＣＧ、辺ＥＦ、辺ＧＨ。
イ・ウ・オ。

（２）　30.5％！

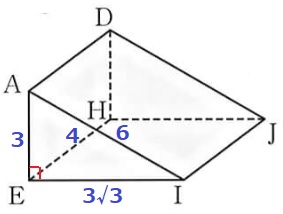
ＡＩ//ＤＪから立体①は三角柱。
△ＡＥＩで三平方→ＥＩ＝３√３ｃｍ
側面積は展開図をイメージし、３つの長方形を合わせて計算する。
３√３×３÷２×２＋（３＋６＋３√３）×４
＝36＋21√３ｃｍ²

（３）　4.3％!!
最短距離は展開図。

面ＪＩＡＤを左側へ折りかえす。
△ＪＣＦ∽△ＰＢＦより、ＰＢ＝14×３/７＝６ｃｍ

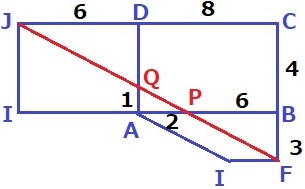
ＡＰ＝８－６＝２ｃｍ
△ＡＱＰ∽△ＦＢＰより、ＡＱ：ＡＰ＝ＢＦ：ＢＰ＝１：２でＡＱ＝１ｃｍ
△ＡＰＱで三平方→ＰＱ＝√５ｃｍ

（４）　0.5％!!!
面の軌跡。経験の差と時間をどれだけ残せたかで決着がつく。
奥行きは４ｃｍで一定なので、正面からみたときの辺ＡＥの軌跡から考える。

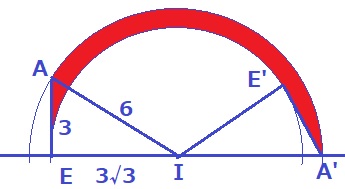
↑こんな感じになる。
とりあえず、中心角が欲しい。
直角三角形ＡＥＩの辺の比は、３：６：３√３＝１：２：√３なので、
内角は30°－60°－90°。

移植。
外径は６ｃｍ、内径は３√３ｃｍ、中心角は150°。
求めたいのは体積なので、最後に奥行き４ｃｍをかけるのを忘れないように！
（６×６×π×150/360－３√３×３√３×π×150/360）×４
＝（９π×５/12）×４
＝15/４π×４＝15πｃｍ³