2024年度　栃木県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）　97.2％
（－４）×（－３）
＝12

（２）　85.0％
√28＋√７
＝２√７＋√７
＝３√７

（３）　45.6％
絶対値…数直線上で原点０からの距離。
絶対値が３より小さい⇒－２、－１、０、１、２の５個。
（＊－３、３は含めない）

（４）　67.7％
ｘ²＋５ｘ＋６
＝（ｘ＋３）（ｘ＋２）＝０
ｘ＝－３、－２

（５）　80.9％
反比例はｘとｙの積が比例定数ａで一定。
ａ＝－３×２＝－６

（６）　45.4％
半径は２ｃｍで共通→中心角の比で考える。
円周：扇形の弧＝360°：40°＝９：１
扇形の弧の長さは、円周の長さの１/９倍。

（７）　46.1％
【球の体積Ｖ＝４/３πｒ³】
４/３π×６³＝288πｃｍ³

（８）　69.5％
度数が最も多い階級→85～100回の７人
７/20＝35/100＝0.35

大問２（小問集合２）

（１）　40.8％
小数第１位を四捨五入して29となる範囲を求める。
28.5から29になり、29.5から30になる。
28.5≦ａ＜29.5

（２）　52.0％（部分正答含む71.8％）
答案では走る距離をｘｍ、歩く距離をｙｍとして連立方程式をつくり、途中の計算も書く。
距離で等式。
ｘ＋ｙ＝400　…①
時間で等式。
ｘ/300＋ｙ/60＝２　…②

②を300倍して、ｘ＋５ｙ＝600　…③
③－①をすると、４ｙ＝200
ｙ＝50
①に代入、ｘ＋50＝400
ｘ＝350
走る距離…350ｍ、歩く距離…50ｍ

（３）　38.5％（部分正答含む60.4％）
いつも２になる→定数項２だけを残す。
—–
ｎ²＋（ｎ＋２）²－２（ｎ＋１）²
＝ｎ²＋ｎ²＋４ｎ＋４－２ｎ²－４ｎ－２
＝２
したがって、連続する３つの自然数で、最も小さい数の２乗と最も大きい数の２乗の和から、
中央の数の２乗の２倍をひくと、つねに２となる。

＠余談＠

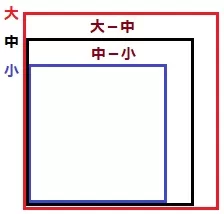
平方数を図形で描くと正方形。
連続する３つの自然数の平方数を小さい順に小・中・大の正方形で表す。
大＋小－中×２
＝（大－中）＋（小－中）
＝（大－中）－（中－小）
つまり、（大－中）のＬ字と（中－小）のＬ字の差が２になるはずである。

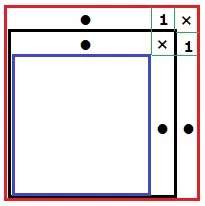
このように相殺すると２つのＬ字の差は２。

大問３（平面図形）

（１）　54.5％

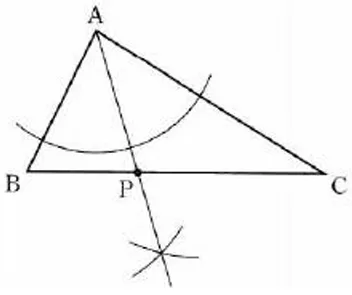
『２辺ＡＢ・ＡＣから等距離にある』→∠ＢＡＣの二等分線
これとＢＣとの交点がＰ。

（２）①　72.6％
△ＡＤＣは内角から直角二等辺三角形。
辺の比は１：１：√２→ＡＤ＝５√２ｃｍ

②　8.0％!!

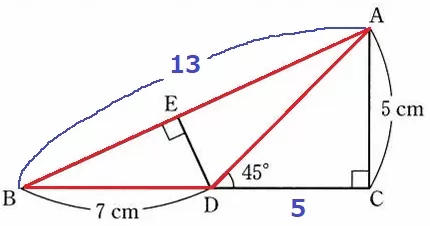
ＤＥは底辺をＡＢとみたときの△ＡＢＤの高さにあたる。
△ＡＢＣで三平方→ＡＢ＝13ｃｍ（辺の比が５：12：13の直角三角形）
△ＡＢＤの面積を２通りで示すと、
【ＢＤ×ＡＣ÷２＝ＡＢ×ＤＥ÷２】
７×５＝13×ＤＥ
ＤＥ＝７×５÷13＝35/13ｃｍ

（３）　5.0％!!（部分正答含む63.7％）
△ＡＢＣ≡△ＤＣＢの証明。

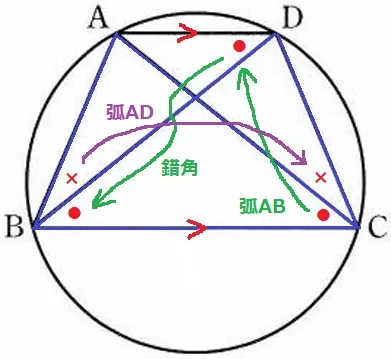
共通辺ＢＣ。
弧ＡＢの円周角→ＡＤ//ＢＣの錯角で、∠ＡＣＢ＝∠ＤＢＣ（●）
弧ＡＤの円周角で、∠ＡＢＤ＝∠ＡＣＤ（×）
よって、∠ＡＢＣ＝∠ＤＣＢ（●＋×）
１辺と両端角が等しいので合同。

大問４（データの活用・確率）

（１）①　35.1％
25～30分の階級値→27.5分

②　50.3％

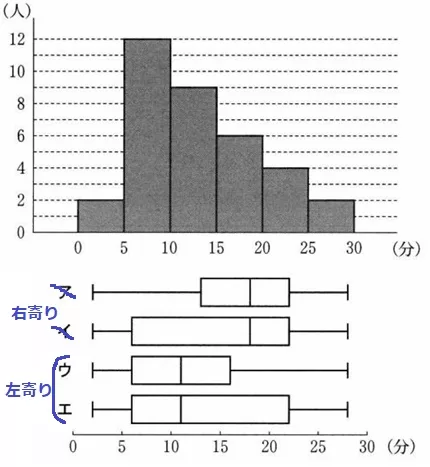
ヒストグラムを俯瞰すると、データが左に寄っている。
この時点で中央値が右に寄るア・イが消える。
残りのウ・エで異なる第３四分位数（Q3）に着目する。
35人の中央値は18番目。Q3は上位17人の真ん中、上から９番目。
15～20分の階級に含まれるのでウ。

（２）①　58.7％
Ａは５通り、Ｂは残りの４通り。
５×４＝20通り

②　37.8％
今度はＡが玉を戻すので、全体は５×５＝25通り
７以下より８以上の方が少ないので、余事象から攻める。
８以上の組合わせは（Ａ、Ｂ）＝（３、５）（４、４～５）（５、３～５）の６通り。
確率は、１－６/25＝19/25

大問５（関数・数量変化）

（１）①　56.6％
ｙ＝－ｘ²について、
ｘ＝０のとき、最大値ｙ＝０
ｘ＝－３のとき、最小値ｙ＝－９
－９≦ｙ≦０

②　12.8％！（部分正答含む74.4％）

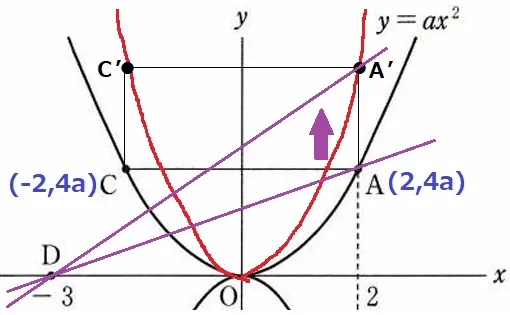
ｙ＝ａｘ²のａの絶対値を大きくすると、グラフの開きは小さくなる。
座標をａで示すと、Ａ（２、４ａ）Ｃ（－２、４ａ）
４ａの値が大きくなるから、Ａ座標は上にあがる。
ＡＤはより急になるので傾きは大きくなる。
しかし、ＡＣの長さは２－（－２）＝４で一定である。
①…ア、②…ウ

③　20.3％！（部分正答含む31.3％）
答案では途中の計算も書く。

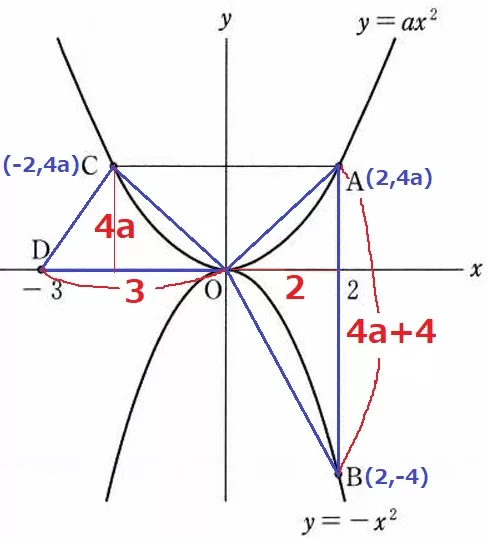
必要な長さは上図の通り。
△ＯＡＢの面積は、（４ａ＋４）×２÷２＝４ａ＋４
△ＯＣＤの面積は、３×４ａ÷２＝６ａ
これらが等積なので、４ａ＋４＝６ａ
ａ＝２

（２）①　41.9％（部分正答含む70.4％）

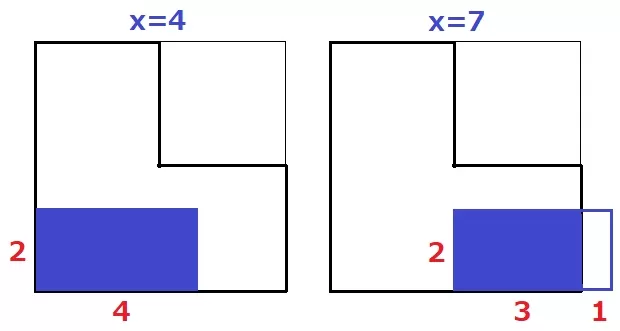
ｘ＝４のとき、ｙ＝２×４＝８
ｘ＝７のとき、ｙ＝２×３＝６
①…８、②…６

②　33.3％
長方形ＡＢＣＤが縦長になる。

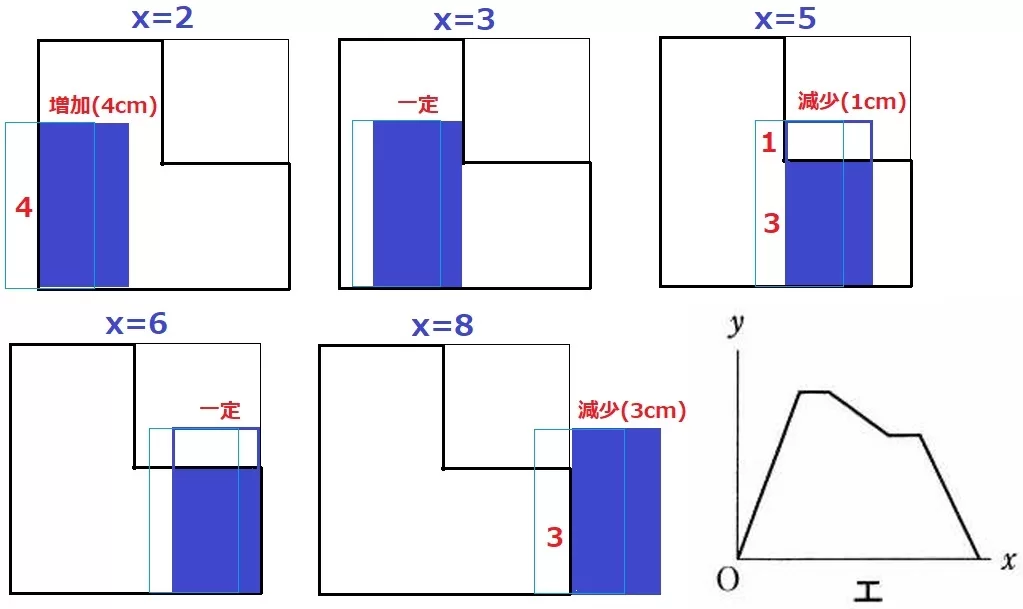
０≦ｘ≦２、高さ４ｃｍずつ中に入る。
２≦ｘ≦３、面積は一定。
３≦ｘ≦５、高さ１ｃｍずつ外に出る。
５≦ｘ≦６、一定
６≦ｘ≦８、高さ３ｃｍずつ外に出る。
一定が２ヵ所あるエ。

③　6.0％!!（部分正答含む12.1％）
答案では途中の計算も書く。

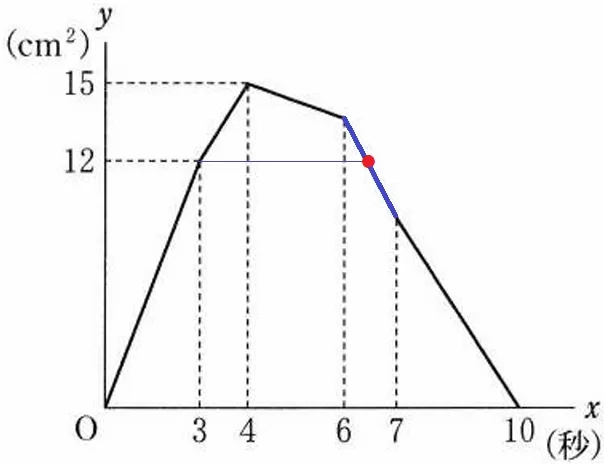
ｘ＝３のとき、グラフからｙ＝12とわかる。
再びｙ＝12になるのは６≦ｘ≦７のとき。
この直線の式を求め、ｙ＝12を代入すれば求めたいｘがでる。

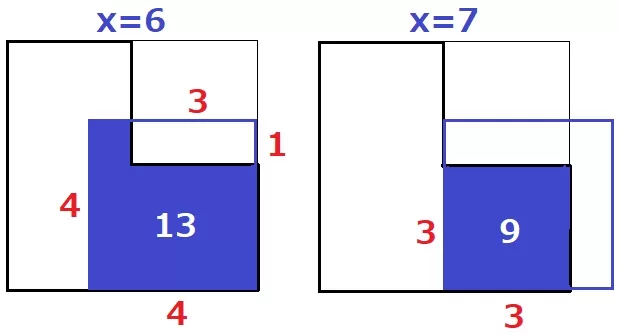
ｘ＝６のとき、ｙ＝４×４－３×１＝13
ｘ＝７のとき、ｙ＝３×３＝９
（６、13）→（７、９）
右に１、下に４だから、傾きは－４。
ｙ＝－４ｘ＋ｂに（７、９）を代入すると、
９＝－28＋ｂ
ｂ＝37

最後に、ｙ＝－４ｘ＋37にｙ＝12を代入。
12＝－４ｘ＋37
ｘ＝25/４
25/４秒後

＠余談＠

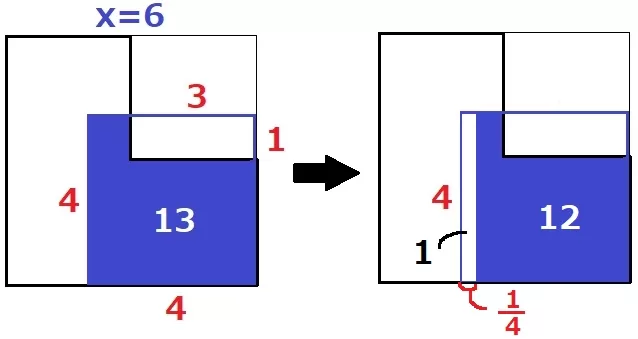
ｘ＝６のとき、ｙ＝13だったので、重なりをあと１ｃｍ²減らせばｙ＝12になる。
減少すべき長方形の横の長さは、１÷４＝１/４ｃｍ
よって、６＋１/４＝25/４秒後

大問６（文字式）

（１）　77.8％
92÷４＝18列…２人
余りの２人は次の列→19列

（２）　45.7％
●新幹線●
５×24＝120人
最後の列が５人フルで座って120人。
最後の列が１～４人欠ける場合もある→範囲は116～120人
（*115人だと23列になってしまう）
●タクシー●
４×29＝116人
最後のタクシーが１～３人欠ける場合もある→範囲は113～116人
（*112人だと28台になってしまう）
範囲が重複する116人。

（３）　0.1％!!!（部分正答含む8.6％）
新幹線の列をｎとする。
最終列はａ人（１～５の自然数）、それ以外のｎ－１列は５人ずつ座る。
生徒の人数は、５（ｎ－１）＋ａ人（①）

タクシーの台数はｎ＋10台。
タクシーの最後はｂ人（１～４の自然数）、それ以外の（ｎ＋10）－１＝ｎ＋９台は４人ずつ座る。
生徒の人数は、４（ｎ＋９）＋ｂ人
生徒の人数で等式を立て、ｎについて解く。
５（ｎ－１）＋ａ＝４（ｎ＋９）＋ｂ
５ｎ－５＋ａ＝４ｎ＋36＋ｂ
ｎ＝41－ａ＋ｂ（②）

いったん情報を整理。
新幹線の列がｎ、ａ＝１～５の自然数、ｂ＝１～４の自然数。
生徒の人数を最も少なくする→新幹線の列ｎが最も小さい。
ｎ＝41－ａ＋ｂの値が最も小さくなるのはａ＝５、ｂ＝１のとき。
ｎ＝41－５＋１＝37
生徒の人数は５（ｎ－１）＋ａにｎ＝37、ａ＝５を代入する。
５×（37－１）＋５＝185人（③）
（＊４（ｎ＋９）＋ｂにｎ＝37、ｂ＝１を代入してもいい）
①…５（ｎ－１）、②…41－ａ＋ｂ、③…185