2021年度　富山県公立高校入試問題過去問【数学】解説

平均47.0点（前年比；－0.1点）
問題はコチラ→ＰＤＦファイル
出題範囲の削減はなし。

大問１（小問集合）

（１）
７－２×８
＝７－16
＝－９

（２）
２ｙ²÷ｘｙ×５ｘ²ｙ
＝10ｘｙ²

（３）
√６×√２－√３
＝２√３－√３
＝√３

（４）
３（２ａ－３）－４（ａ－２）
＝６ａ－９－４ａ＋８
＝２ａ－１

（５）
反比例の比例定数ａは積ｘｙで一定。
ｙ＝６×４÷（－３）＝－８

（６）
ｘ²－11ｘ＋28
＝（ｘ－４）（ｘ－７）＝０
ｘ＝４、７

（７）
「ある数ｘを３倍した数」⇒３ｘ
「ある数ｙから４を引いて５倍した数」⇒５（ｙ－４）
（*引き算→掛け算の順）
３ｘ＜５（ｙ－４）

（８）
全体は、６×６＝36通り
和が３の倍数となる組み合わせを場合分けして調べる。
■和が３→（１、２）と逆を含めて２通り。
■和が６→（１、５）（２、４）とこれらの逆と（３、３）で５通り。
■和が９→（３、６）（４、５）とこれらの逆で４通り。
■和が12→（６、６）で１通り。
計12通り。
確率は12/36＝１/３

（９）

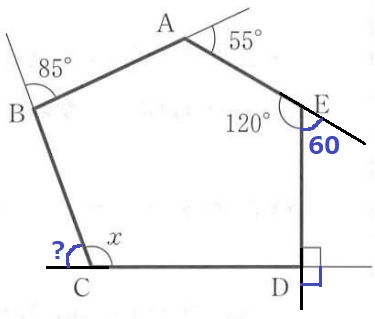
多角形の外角の和は360°
？＝360－（85＋55＋60＋90）＝70°
ｘ＝180－70＝110°

（10）
作図。
『２点Ａ、Ｂからの距離が等しい』→点ＰはＡＢの垂直二等分線上にある。
これと直線ℓとの交点がＰとなる。

大問２（関数）

（１）
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－４のとき、最大値ｙ＝８
０≦ｙ≦８

（２）

２本の赤線の範囲内にあれば、青いウネウネと交わる。
Ａ（－２、２）⇒Ｂ（４、８）
右に６、上に６だから、傾きは６/６＝１
Ａ（－２、２）⇒Ｃ（６、18）
右に８、上に16だから、傾きは16/８＝２
４≦ｘ≦６なので、ＢとＣも範囲に含まれる。
１≦ａ≦２

（３）

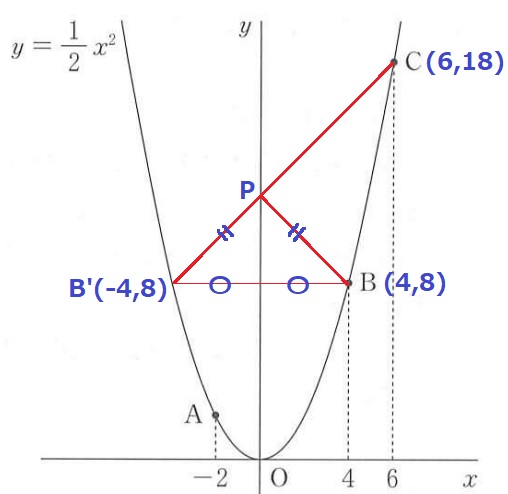
ＢＰ＋ＣＰが最小→直線にする→線対称。
Ｂをｙ軸について対称移動した点をＢ’とすると、ＢＰ＝Ｂ’ＰでＢ’Ｃが最短距離。
Ｂ’Ｃとｙ軸との交点がＰである。

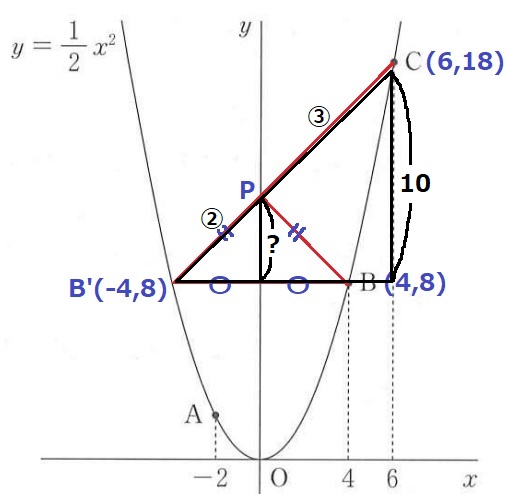
ｘ座標の差から、Ｂ’Ｐ：ＰＣ＝４：６＝②：③
Ｂ’とＣのｙ座標の差が10だから、∽を利用して？＝10×②/⑤＝４
Ｐのｙ座標は、８＋４＝12
Ｐ（０、12）

大問３（規則）

（１）
１段目→１枚＝１×１
２段目まで→１＋３＝４枚＝２×２
３段目まで→１＋３＋５＝９枚＝３×３
４段目まで→１＋３＋５＋７＝16枚＝４×４…
連続する奇数の和→最後の奇数が〇番目の奇数なら『〇の平方数』にあたる。
７段目の右端は７番目の奇数だから、７段目までの枚数は７×７＝49枚

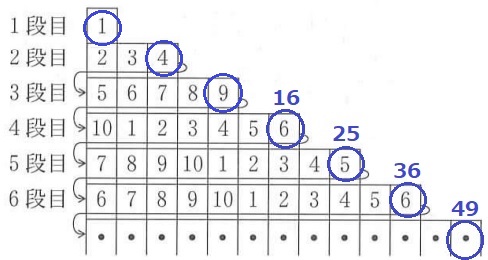
右端には平方数が連なり、４段目以降は平方数の一の位を抜き出している。
７段目の右端は７×７＝49なので、その一の位の９。
49枚、９

（２）
一の位が６となる平方数は、４×４か６×６のどちらか。
３回目は14×14＝196
よって、14段目。
*４回目は16×16、５回目は24×24…。
20×20までの平方数は覚えておきましょう。

（３）
先ほどの数値の一の位をみると、
〔１・４・９・６・５・６・９・４・１・０〕がループする。
ループに現れない２、３、７、８が答え。

大問４（データの活用）

（１）①
１つ目は人数で等式。
32－（０＋８＋２＋４）＝18人
ｘ＋ｙ＝18

２つ目はソフトボールの飛距離で等式。
全体の記録の合計は、30×32＝960ｍ
20～40ｍの階級値×度数の合計は、960－（０＋120＋90＋220）＝530ｍ
階級値は20～30ｍ→25ｍ、30～40ｍ→35ｍなので、
25ｘ＋35ｙ＝530
ｘ＋ｙ＝18、25ｘ＋35ｙ＝530

②
先の連立を解く。
ｘ＋ｙ＝18　…①
25ｘ＋35ｙ＝530　…②
②－①×25をすると、10ｙ＝80
ｙ＝８
①に代入して、ｘ＝10
ｘ＝10、ｙ＝８

（２）
ア：最頻値（モード）は最もあらわれている値。Ａは18分、Ｂは21分でＡの方が小さい。×
イ：Ｂより０分以上６分未満が５人、Ａより０分以上４分未満が４人。
　ということは、４分以上６分未満は５－４＝１人。〇
ウ：即答しづらい。

　数直線を使って調べてみる。〇が含まない、●が含む。
９～18分の範囲のうち、12～18分の７人は確定。
８～12分の２人が９～12分にいたら、９～18分の最大人数は２＋７＝９人〇
エ：Ａは３＋８＋６＝17人、Ｂは７＋10＝17人で同じだから相対度数の和も同じ。×
階級の幅が違っても、始めと終わりの範囲が等しければ人数も割合も等しい。
イ、ウ

大問５（空間図形）

（１）

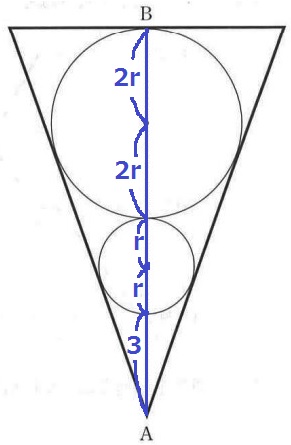
ＡＢ＝12ｃｍだから、
２ｒ＋２ｒ＋ｒ＋ｒ＋３＝６ｒ＋３＝12
ｒ＝３/２

（２）

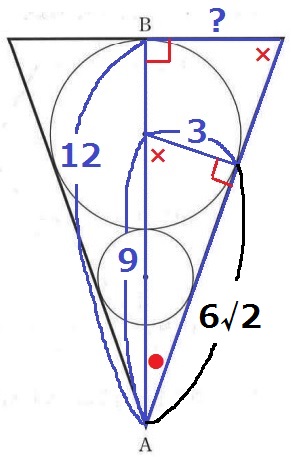
半径と接線は垂直に交わる。他県でも見かける相似である。
辺の長さが整数値である大きい球の半径３ｃｍを使う。
三平方の定理で、√（９²－３²）＝６√２ｃｍ
【３：６√２＝？：12】
？＝３×12÷６√２＝３√２ｃｍ

（３）

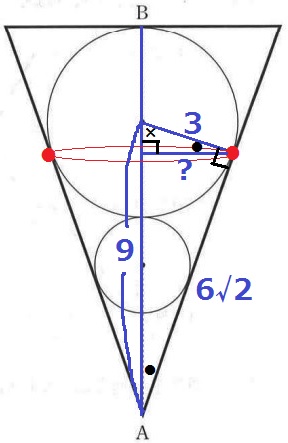
大きい球が容器の側面に接している部分が●で、これを通る円の円周を求める。
この円の半径が知りたい。
直角三角形の直角から対辺に垂線をひくと直角三角形の相似ができる（頻出！）
【９：６√２＝３：？】
？＝６√２×３÷９＝２√２ｃｍ
円周の長さは、２√２×２π＝４√２πｃｍ

大問６（数量変化）

（１）
普通列車はＡＢ間10ｋｍを10分で走る。
１時間（60分）では、10ｋｍ×60/10＝時速60ｋｍ

（２）
特急列車は時速80ｋｍ→60分で80ｋｍ進む。
ＡＣ間を30－12＝18分間で走るので、80ｋｍ×18/60＝24ｋｍ

（３）

ＢＣ間は24－10＝14ｋｍ
12分後から普通と特急は１時間当たり80＋60＝140ｋｍずつ近づいていく。
両者が出会う時間は、14÷140＝１/10時間
Ａ駅からの距離は、10＋60×１/10＝16ｋｍ

＠別解＠

こちらも中学受験の戦法です。
Ｂ駅での休憩２分をなくして、普通列車が２分後から走ったとします。
普通列車は時速60ｋｍの速さだから、24ｋｍでは24分後の26分にＣ駅へ着きます。
青線の三角形で相似を使います。14：28＝①：②
よって、24ｋｍ×②/③＝16ｋｍ

（４）

●のところで普通と特急が出会う。？が知りたい時間。

右上の部分だけで決着が着く。
ＢＣ間は14ｋｍで、普通は14/60時間、特急は14/80時間かかる。
これを分に直して、普通の休憩２分を足せばいい。
60×14/60＋60×14/80＋２
＝14＋10.5＋２＝26.5分＝26分30秒
午前９時40分から26分30秒後は午前10時６分30秒。

大問７（平面図形）

（１）
△ＡＢＣ≡△ＡＧＥの証明。

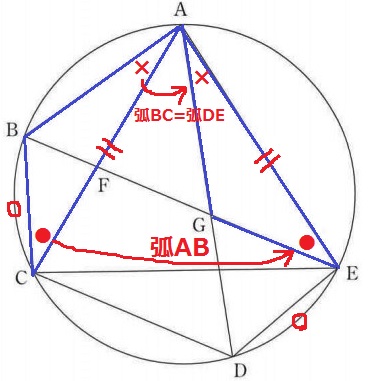
仮定より、ＡＣ＝ＡＥ
弧ＡＢに対する円周角で、∠ＡＣＢ＝∠ＡＥＧ（●）
弧ＢＣ＝弧ＤＥに対する円周角で、∠ＢＡＣ＝∠ＧＡＥ（×）
１辺と両端角が等しいから合同。

（２）①

（１）の合同から、ＡＧ＝ＡＢ＝４ｃｍ
ＡＦを１辺とする三角形と相似にあたる三角形を探す。
右側の数値がわかっている。△ＡＤＥが怪しい…。
弧ＡＥに対する円周角で、∠ＡＢＦ＝∠ＡＤＥ（●）
弧ＢＣ＝弧ＤＥより、∠ＢＡＦ＝∠ＤＡＥ（×）
２角相等で△ＡＢＦ∽△ＡＤＥ

ＡＢ：ＡＦ＝ＡＤ：ＡＥ
４：ＡＦ＝７：６
ＡＦ＝４×６÷７＝24/７ｃｍ

②

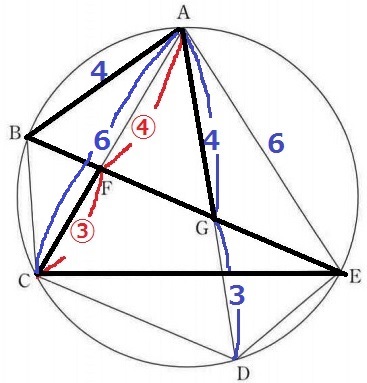
△ＡＢＧと△ＣＥＦは全然相似じゃない(;`ω´)
前問のＡＦ＝24/７ｃｍを利用する。
ＦＣ＝６－24/７＝18/７ｃｍ
ＡＦ：ＦＣ＝24/７：18/７＝④：③
ここからどうするか。。
ＡＣ：ＦＣ＝△ＡＣＥ：△ＣＥＦで、△ＡＣＥは△ＡＢＧと同じ二等辺三角形…。

弧ＡＥに対する円周角で、∠ＡＢＧ＝∠ＡＣＥ（●）
二等辺の底角が等しいので、△ＡＢＧ∽△ＡＣＥ
相似比は４：６＝２：３
面積比は相似比の２乗だから、△ＡＢＧ：△ＡＣＥ＝４：９
△ＡＣＥ：△ＣＥＦ＝⑦：③、△ＣＥＦ＝９×③/⑦＝27/７
よって、△ＡＢＧ：△ＣＥＦ＝４：27/７＝28：27