平均47.1点（前年比；－7.2点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
７＋４×（－２）
＝７－８
＝－１
（２）
ｘｙ3×６ｘ2ｙ÷３ｙ2
＝２ｘ3ｙ2
（３）
√24－√６
＝２√６－√６
＝√６
（４）
８ａ＋４ｂ－（５ａ－ｂ）
＝８ａ＋４ｂ－５ａ＋ｂ
＝３ａ＋５ｂ
（５）
２ｘ＋３ｙ＝４ …①
５ｘ＋４ｙ＝３ …②
①×５－②×２をすると、７ｙ＝14
ｙ＝２
①に代入、ｘ＝－１
ｘ＝－１、ｙ＝２
（６）
回転体は円柱になる。
３×３×π×10＝90πｃｍ3
（７）
ｙ＝ａｘ2において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（２＋６）＝12
８ａ＝12
ａ＝３/２
（８）
大人４人…４ａ円、子供３人…３ｂ円
これらの合計が7000円以下だから、４ａ＋３ｂ≦7000
（９）
５個から２個を取り出す→5Ｃ2＝10通り
余事象で攻める。２数の積が奇数なのは【奇数×奇数】の組み合わせしかない。
３個の奇数から２個を取り出す→選ばない１個を選ぶ→３通り
積が偶数となる確率は、１－３/10＝７/10
（10）
ＡＢをＡＣに重ねる→折り目ＡＰが対称の軸。
∠ＣＡＢの二等分線をひき、ＢＣとの交点がＰ。
大問２（方程式）
（１）
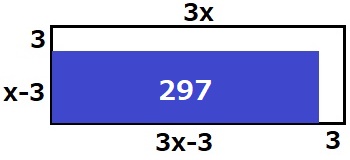
畑の面積で等式を立てる。畑を端に寄せる。
（ｘ－３）（３ｘ－３）＝297
①…ｘ－３、②…３ｘ－３
（２）
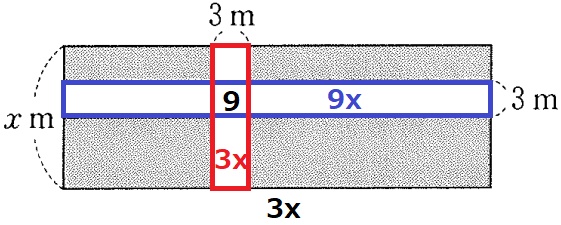
今度は道の面積で等式を立てる。
横の長方形が９ｘ、縦の長方形が３ｘ。重複する交差の９ｍ2をひく。
９ｘ＋３ｘ－９＝12ｘ－９＝３ｘ2－297
③…12ｘ－９
（３）
前問の方程式を解く。
12ｘ－９＝３ｘ2－297
３ｘ2－12ｘ－288＝０ ←÷３
ｘ2－４ｘ－96
＝（ｘ－12）（ｘ＋８）＝０
ｘ＞３だから、ｘ＝12
12ｍ
大問３（データの活用）
（１）
四分位範囲＝第３四分位数－第１四分位数
＝11－３
＝８問
（２）①
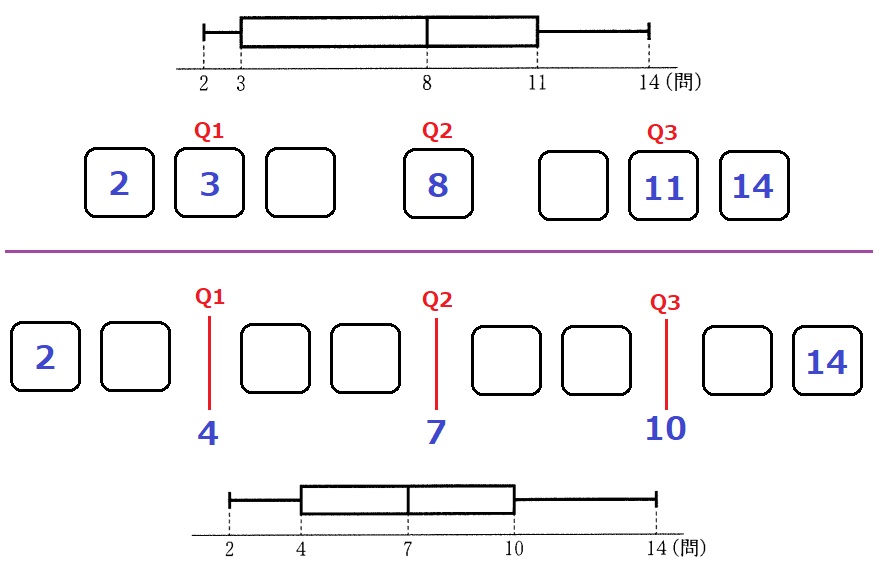
箱ひげ図をもとにマス目を書いてみる。
最初の７人のうち、５人は数値が判明する。
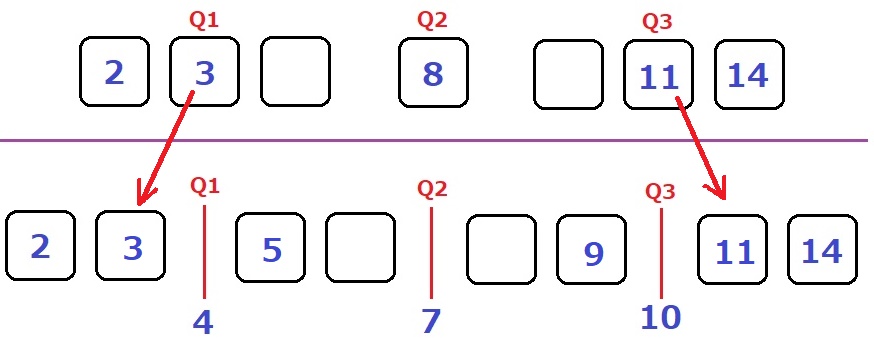
８人のQ1より２番目が３、Q3より７番目が11と確定。
同じくQ1より３番目は５、Q3より６番目は９と決まる。
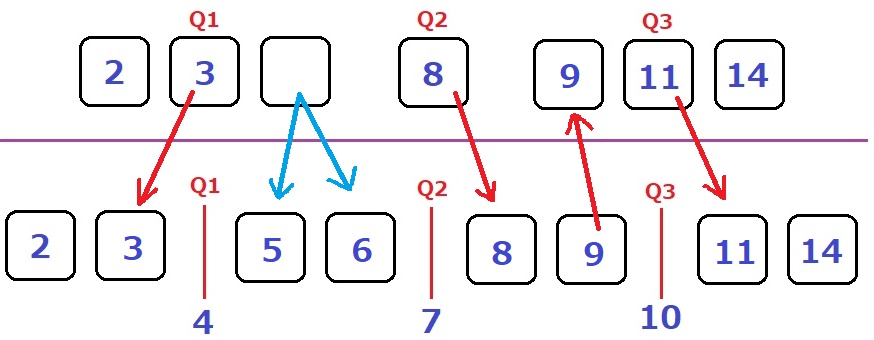
８人のQ2から５番目が８→４番目が６。
７人の５番目は９である。
７人の３番目が５or６が決まらない→みずきは５か６である。
５、６
②
各四分位数は隣同士の平均。
総和…（４＋７＋10）×２＋２＋14＝58
平均値は、58÷８＝7.25問
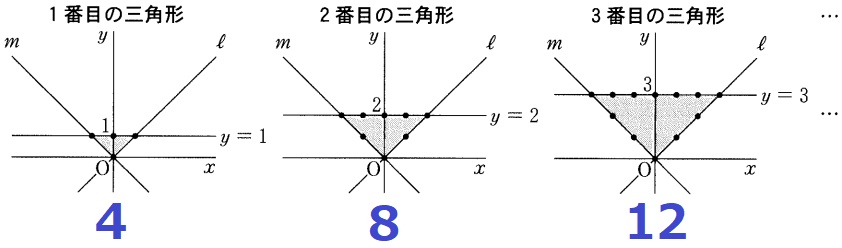
大問４（規則）
（１）①
４の倍数がつづく。
５番目は４×５＝20個
②
ｎ番目は４ｎ個
（２）
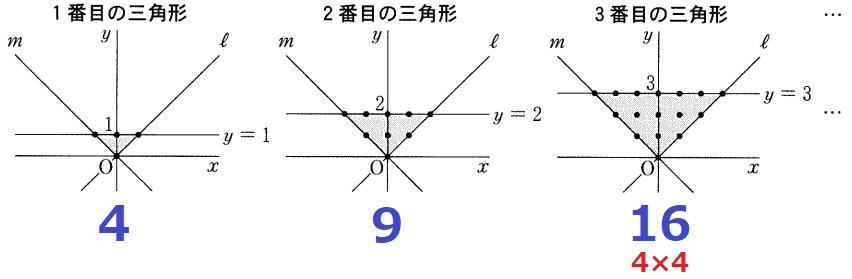
平方数が並ぶ。
３番目→４×４（〇番目＋１の平方数）である点に注意！
14×14＝196→13番目の三角形。
200を超えるのは14番目の三角形。
大問５（空間図形）
（１）
△ＡＣＭで三平方→ＡＭ＝√（７2－２2）＝３√５ｃｍ
（２）
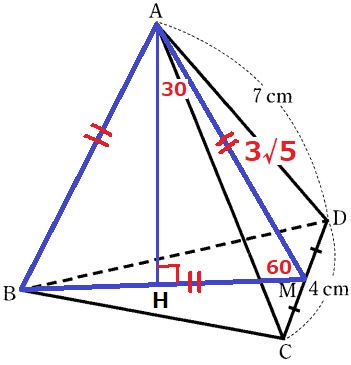
仮定より、△ＡＢＭは正三角形。
Ａから垂線をおろし、底面との交点をＨとする。
ＡＣ＝ＡＤ＝ＢＣ＝ＢＤ＝７ｃｍ
面ＡＢＭを対称面とおくと図形全体が左右対称→ＨはＢＭ上にある。
△ＡＭＨの辺の比は１：２：√３→ＡＨ＝３√５×√３/２＝３√15/２ｃｍ
底面は△ＢＣＤ＝△ＡＣＤ
三角錐の体積は、４×３√５÷２×３√15/２÷３＝15√３ｃｍ3
（３）
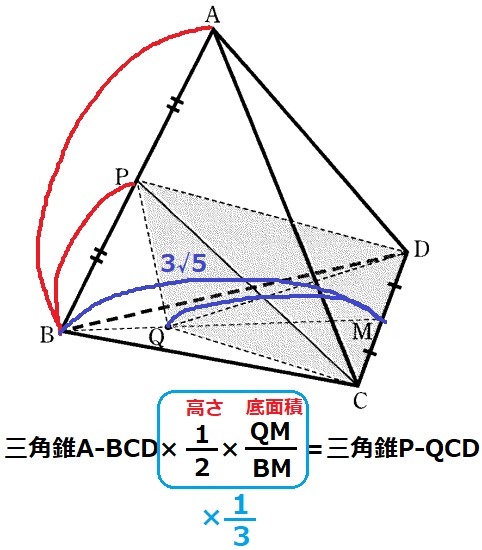
三角錐Ａ―ＢＣＤと三角錐Ｐ―ＱＣＤの高さの比は、ＡＢ：ＰＢ＝２：１
底面積の比は、△ＢＣＤ：△ＱＣＤ＝ＢＭ：ＱＭ（底辺ＣＤが共通→高さの比が面積比）
三角錐Ａ―ＢＣＤ（×１/２×ＱＭ/ＢＭ）＝三角錐Ｐ―ＱＣＤ
１/２×ＱＭ/ＢＭ＝１/３
ＱＭ/ＢＭ＝１/３÷１/２＝２/３→ＱＭ：ＢＭ＝②：③
ＢＭ＝３√５ｃｍなので、ＱＭ＝３√５×②/③＝２√５ｃｍ
大問６（数量変化）
（１）
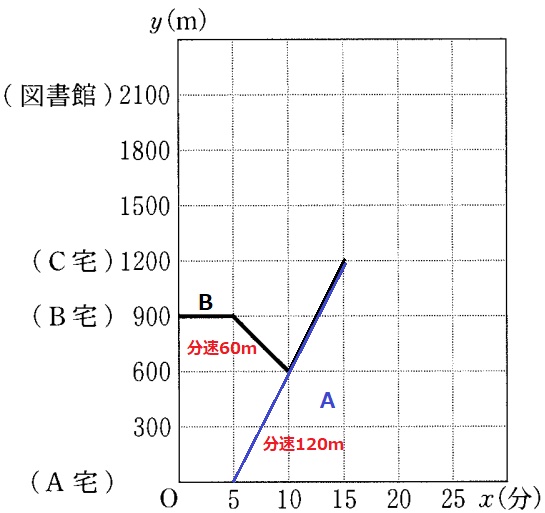
Ｂは５分待ったあと、Ａ宅に向かって５分歩いてＡと出会う。
分速60ｍが右１、下１→分速120ｍのＡは右１、上に２の傾き。
（10、600）の出会いから右１、上に２移動してＣ宅に着く。
図の黒線が答え。（Ａは５分後にＡ宅を出発したことになる）
（２）
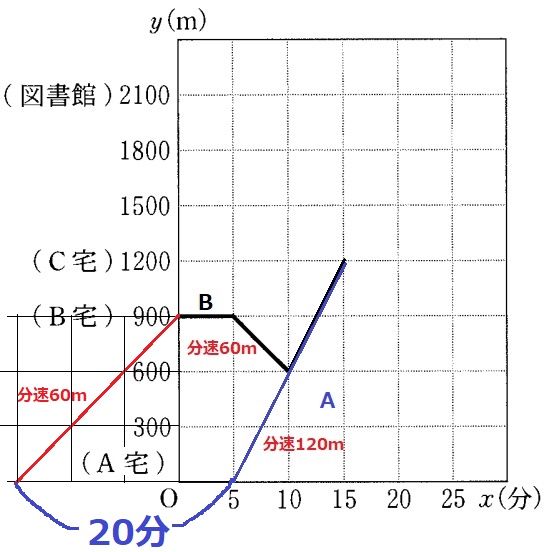
ＡがＢ宅に着く予定は（０、900）だった。
これを通る傾き１マス（分速60ｍ）の直線をひく。
Ａ宅の出発予定時刻は－15分、Ａが実際に出発した時刻は５分なので、
５－（－15）＝20分遅れた。
（３）
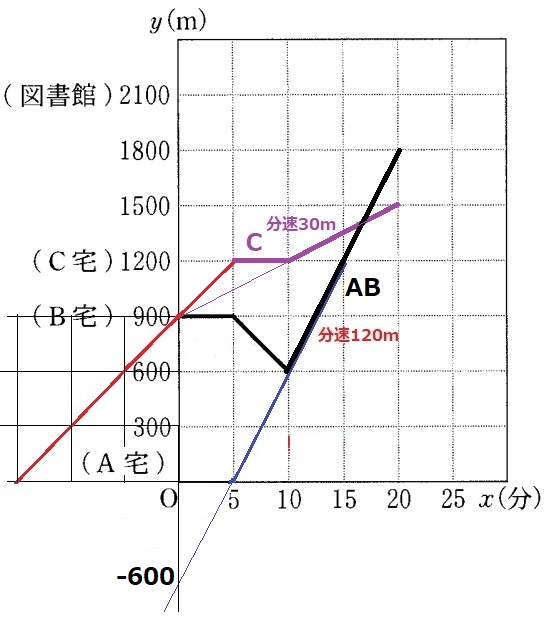
予定の直線を延長。ＡがＣ宅に着く予定は（５、1200）だった。
その５分後にＣが分速30ｍで出発する。
傾き30（左２マス、下１マス）をｙ軸に延長すると切片は900→ｙ＝30ｘ＋900
ＡＢの傾きは120、延長すると切片は－600→ｙ＝120ｘ－600
ＡＢがＣに追いつく交点を求める。
30ｘ＋900＝120ｘ－600
ｘ＝50/３
ｙ＝30ｘ＋900に代入して、
30×50/３＋900＝1400ｍ
（４）
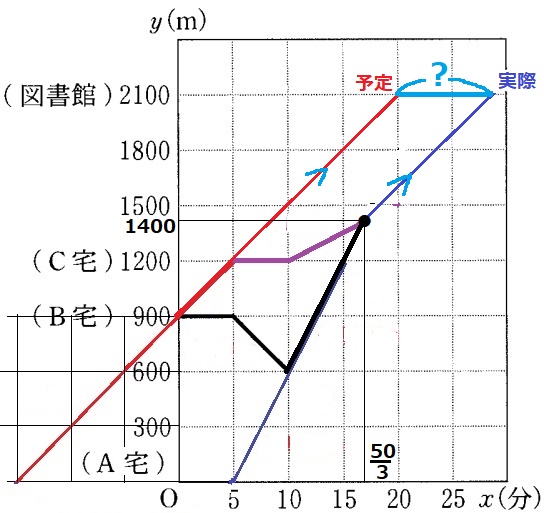
３人がそろった後は分速60ｍで図書館に向かう。
赤線と青線は平行。到着予定時刻との差は？の部分である。
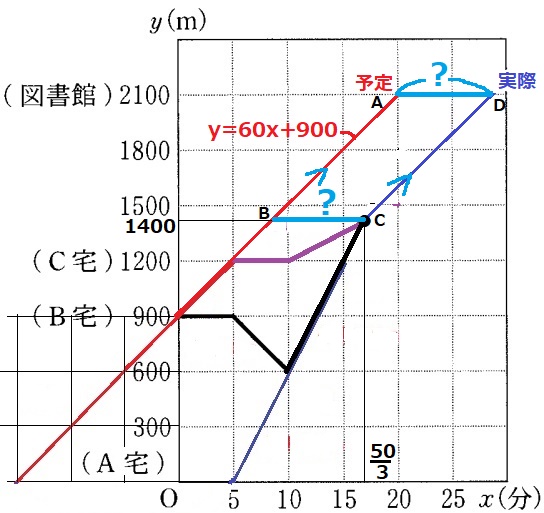
四角形ＡＢＣＤは２組の対辺が平行だから平行四辺形。
対辺は等しいので、ＢＣの長さを求めればいい。
赤線のｙ＝60ｘ＋900にｙ＝1400を代入→Ｂのｘ座標は25/３
ＢＣの長さは、50/３－25/３＝25/３＝８・１/３分＝８分20秒
大問７（平面図形）
（１）
△ＡＥＤ∽△ＡＢＧの証明。
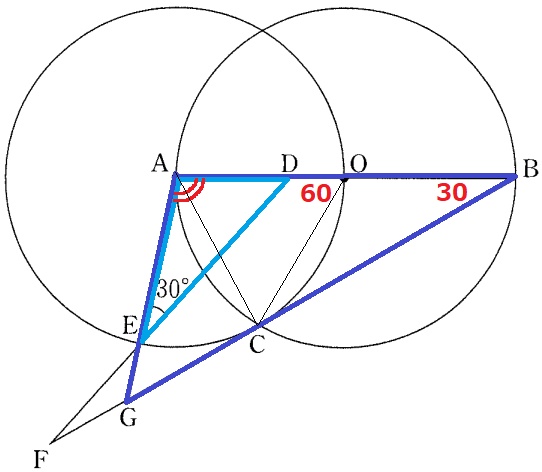
△ＯＡＣは正三角形と求めている。
弧ＡＣに対する円周角から、∠ＡＢＣ＝60÷２＝30°
∠ＡＥＤ＝∠ＡＢＧ＝30°
共通角で∠ＥＡＤ＝∠ＢＡＧ
２角が等しいので∽。
（２）①
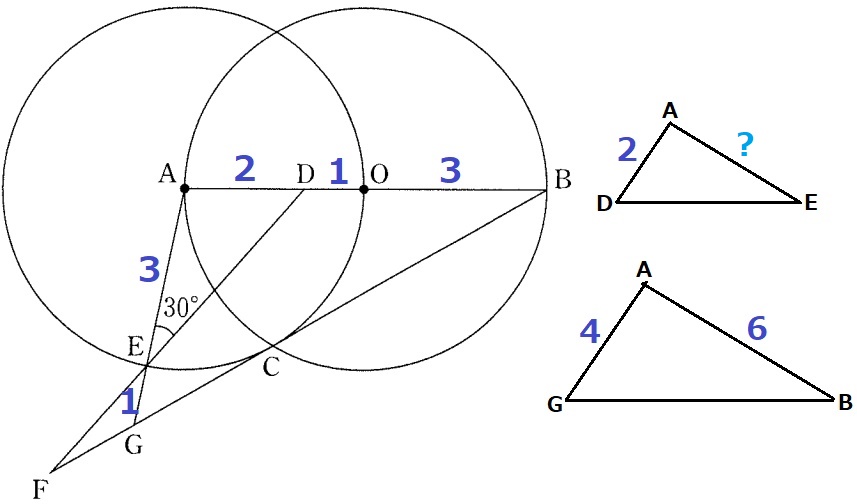
ＡＤ＝６÷３＝２ｃｍ
△ＡＥＤ∽△ＡＢＧより、ＡＥ＝６×２/４＝３ｃｍ
ＢＧに対応するＥＤの長さがわからない。
30°があるので、有名三角形の存在を疑う。
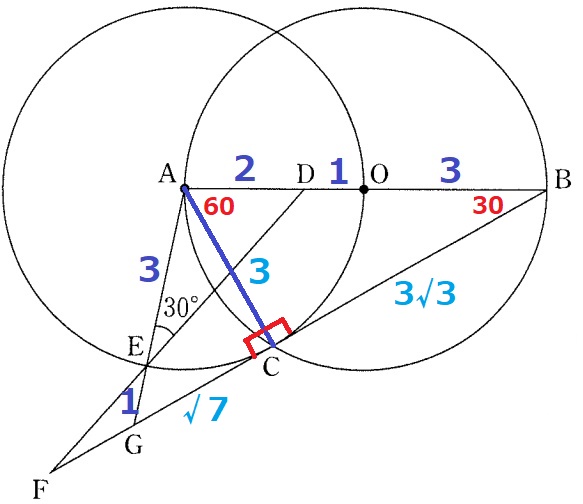
ＡＣに補助線。半円の弧に対する円周角ＡＣＢ＝90°
△ＡＢＣの辺の比は１：２：√３→ＡＣ＝３ｃｍ、ＣＢ＝３√３ｃｍ
△ＡＧＣで三平方→ＧＣ＝√７ｃｍ
ＢＧ＝３√３＋√７ｃｍ
②
△ＥＦＧは外側に出ているので、これと相似にあたる三角形を探す。
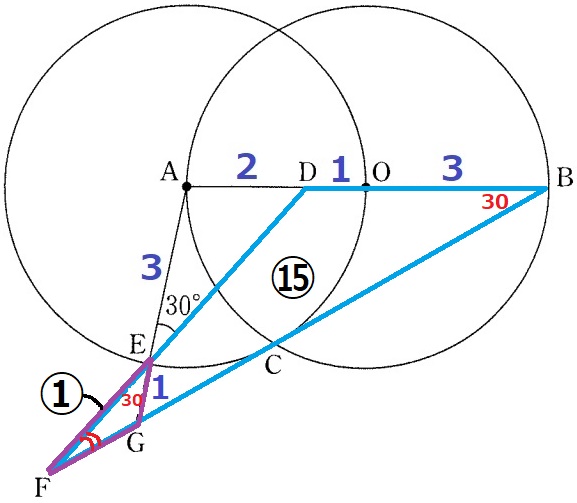
対頂角で30°を移すと、共通角と合わせて２角相等→△ＥＦＧ∽△ＢＦＤ
相似比は、ＥＧ：ＢＤ＝１：４
２乗して面積比は、△ＥＦＧ：△ＢＦＤ＝①：⑯（四角形ＢＤＥＧは⑮）
△ＡＥＤ∽△ＡＢＧの面積比を隣辺比から求める。
△ＡＥＤ：△ＡＢＧ
＝（ＡＥ×ＡＤ）：（ＡＧ×ＡＢ）
＝３×２：４×６
＝１：４
四角形ＢＤＥＧ（⑮）＝３だから、△ＡＢＧ＝⑮×４/３＝⑳
→△ＥＦＧの面積は△ＡＢＧの１/20倍。
（３√３＋√７）×３÷２×①/⑳＝（９√３＋３√７）/40ｃｍ2
大問１
後半に厳しい設問が見られるので、高得点を狙うには迅速に処理したい。
大問２
（２）類題をどこかで見かけた。
普通は端に寄せるが、道の場合は十字の面積を直接求める。
大問３
（２）①推論要素を含み、差がつきやすい。
マスを書いて情報整理、確実なものから埋めていく。
②前問が解けなくても、平均から総和が求まる。最大値と最小値だけ足す。
大問４
（２）比較的わかりやすい規則であった。
連続する奇数和は平方数になる。
大問５
（２）底面の二等辺ＢＣＤをＣＤを軸にして起き上がらせると△ＡＣＤ。
ＢＭ→ＡＭ、Ａからの垂線をおろした交点はＢＭ上にくる。
（３）技術力を要する。高さの比×底面積の比＝１/３で等式。
大問６
各々がどの場所からどっち方向にどれくらいの速さで移動するか。
条件の把握に時間をとられると間に合わなくなる。
前問の利用がつづくので、点差も開きやすい。
（１）Ａをつくる。
ＢがＡと出会う場所、傾き120から直線を決定。600≦ｙ≦1200まで描く。
（２）『ＢさんがＢ宅での待ち合わせ時刻』からｘ分。
Ａの出発予定時刻はＯの左側にある。
（３）予定の直線からＣの出発時刻がわかる。
（４）Ｄの時刻を求めてもいい。
ＣＤ間は2100－1400＝700ｍ、700÷60＝35/３分
Ｄの時刻は、50/３＋35/３＝85/３分
85/３－20＝25/３分→８分20秒
大問７
（２）①相似のあとで差が出る。
ＥＤがなかなか出ない。30°はどこかで垂直をつくると有名三角形になる。
ＡＣに補助線をひくと半円に対する弧が使えるので、ＢＧ＝ＢＣ＋ＣＧに分ける。
②離れている場所にある三角形は∽で回収する。
△ＡＢＧは前問の∽。２つの∽の共通部分である四角形ＢＤＥＧで比を統一する。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント