問題PDF
〔問1〕
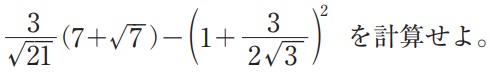
〔問3〕
a、bを1以上6以下の自然数とする。
4個の数a、b、2、6において、中央値と平均値が一致するa、bの組合せは全部で何通りあるか。
〔問4〕
1個のさいころを2回投げるとき、1回目に出た目の数をa、2回目に出た目の数をbとする。
自然数 N について、a、bがともに偶数またはともに奇数のときN=a+b、それ以外のときN=abとする。
Nが4の倍数となる確率を求めよ。ただし、さいころの目の出方は同様に確からしいものとする。
〔問5〕
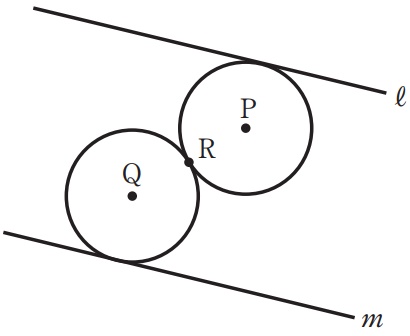
右の図で、直線ℓ、mは平行、直線ℓは円 P の接線である。
円Qは、円Pと半径が等しく、直線 m に接し、円P上の点Rにおける円 P の接線と、点Rで接する。
解答欄に示した図をもとにして、円Qの中心を 1 つ、定規とコンパスを用いて作図し、
中心の位置を示す文字Qも書け。ただし、作図に用いた線は消さないでおくこと。
@解説@
〔問1〕
![]()
=√21+√3-(1+√3+3/4)
=√21-7/4
〔問2〕
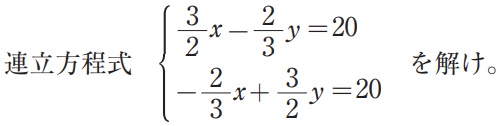
20で値が同じなので、
3/2x-2/3y=-2/3x+3/2y ←6倍
9x-4y=-4x+9y
13x=13y
x=y
上の式のyをxに変える。
3/2x-2/3x=5/6x=20
x=y=24
〔問3〕
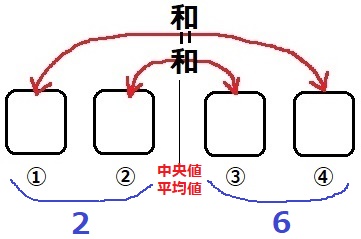
4つを均すと、2番目と3番目の平均である中央値と一致する。
→1番目と4番目を均しても中央値になる。
(1番目+4番目=2番目+3番目)
最大値6は平均以上。
(a、b)=1、1でも平均値は2.5なので、2は平均以下。
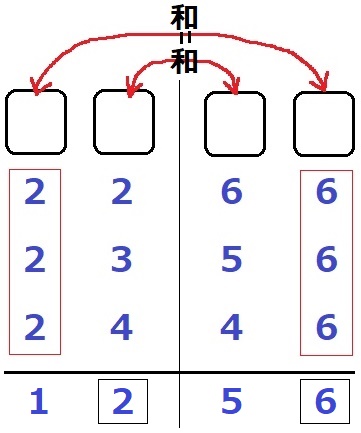
2・6をペアにして両端で固定すると、
(a、b)=(2、6)(6、2)(3、5)(5、3)(4、4)
もう1つは2・6のペアを外す。1+6=2+5しかない。
(a、b)=(1、5)(5、1)
7通り
〔問4〕
N=a+b(偶偶か奇奇)
●和が4→(1、3)(3、1)(2、2)
●和が8→(2、6)(6、2)(3、5)(5、3)(4、4)
●和が12→(6、6)
N=ab(偶奇)
素因数4がいるので偶=4
4×(奇数)の組み合わせである。
(1、4)(4、1)(3、4)(4、3)(4、5)(5、4)
計15通りだから、確率は15/36=5/12
〔問5〕

Rの位置がわかれば、半径のPR=QRからQも特定できる。
なんとなくRは2直線の真ん中にありそう。
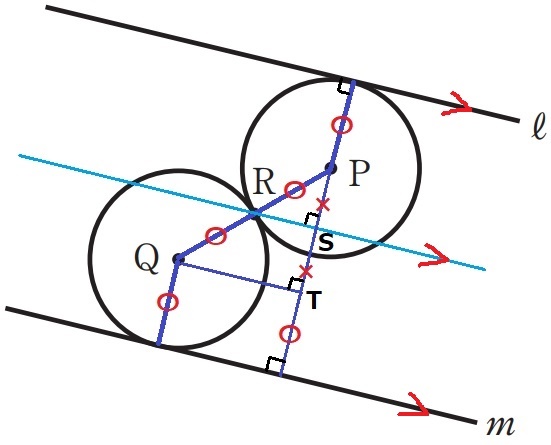
半径〇で中心点と接点を結ぶ。
Rを通る2直線に平行な線をひき、上図の交点をS、Tとすると、
△PRS∽△PQTより、PR:RQ=PS:ST=1:1
Rはℓとmから等距離(〇+×)にある。
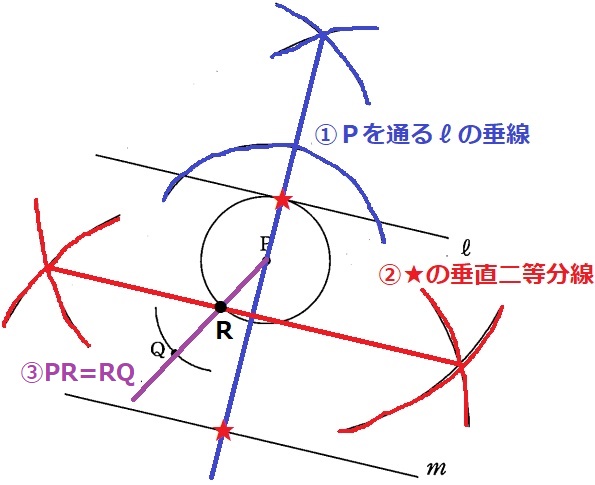
①Pを通る直線ℓの垂線。
②★と★の垂直二等分線が2直線の真ん中の線。円Pとの交点は2つあり、いずれかをRとする。
③直線PR上に半径PRの長さをとり、Qをつくる。


コメント