平均51.7点（前年比；－4.1点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
５ｘ－３ｘ
＝２ｘ
（２）
２×（－４）－１
＝－８－１
＝－９
（３）
６ｘ2ｙ×12ｙ÷４ｘ
＝18ｘｙ2
（４）
５ｘ－７＝６ｘ－３
ｘ＝－４
（５）
√12＋√３
＝２√３＋√３
＝３√３
（６）
ｘ2－ｘ－72
＝（ｘ－９）（ｘ＋８）
（７）
６ｘ－ｙ＝10 …①
４ｘ＋３ｙ＝－８ …②
①×３＋②をすると、22ｘ＝22
ｘ＝１
①に代入、６×１－ｙ＝10
ｙ＝－４
ｘ＝１、ｙ＝－４
（８）
２ｘ2＋７ｘ＋１＝０
解の公式を適用して、ｘ＝（－７±√41）/４
（９）
傾きが２だから、（－３、－２）から右に３、上に６移動して、
切片は－２＋６＝４
ｙ＝２ｘ＋４
（10）
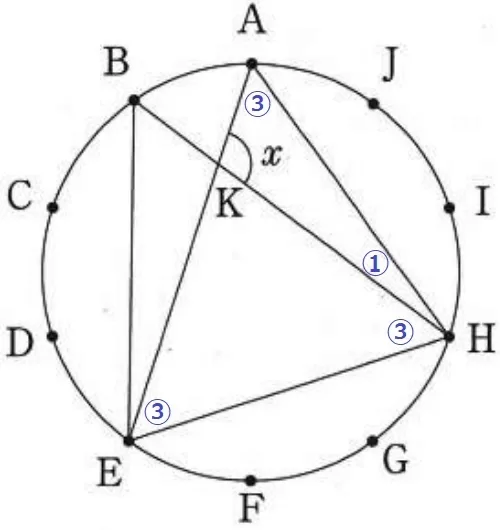
円周角の大きさは弧の長さに比例する。
弧ＡＢは弧１つ分。∠ＡＨＢ＝①とすると、
弧３つ分（弧ＢＥ＝弧ＥＨ＝弧ＨＡ）に対する円周角である、
∠ＢＨＥ＝∠ＥＡＨ＝∠ＨＥＡ＝③
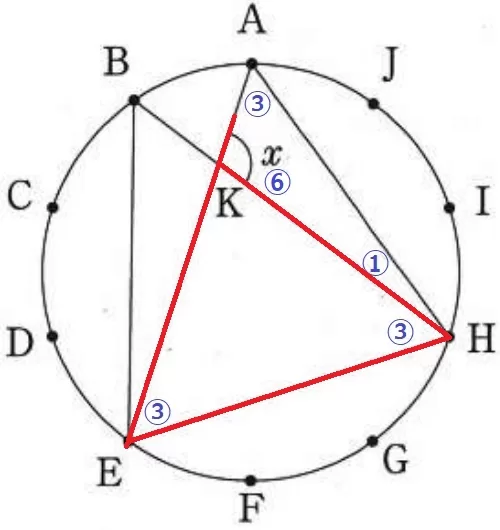
△ＫＥＨで外角定理→ｘ＝③＋③＝⑥
△ＡＢＨの内角より⑩＝180°だから、ｘ＝180×⑥/⑩＝108°
（11）
ＢＣとＥＦを延長、交点をＧとする。
△ＤＥＦの面積を①とする。
△ＤＥＦ∽ＣＧＦより、ＤＦ：ＣＦ＝１：１だから△ＣＧＦ＝①
ＢＣ：ＣＧ＝２：１より、△ＦＢＣ＝②
ＥＦ＝ＦＧより、△ＥＢＦ＝△ＦＢＧ＝③
△ＥＢＦの面積は△ＤＥＦの３倍。
（12）
ア：20人の中央値は10番目と11番目の平均。12～16冊の階級に含まれる。×
イ：８～12冊の度数が４。相対度数は、４/20＝0.20×
ウ：最頻値（モード）は最も現れている値で、12～16冊の階級値である14。×
エ：累積相対度数は、その階級以下の相対度数の合計。
【12～16冊の累積相対度数＝１－16～20冊の相対度数】
16～20冊の相対度数は、３/20＝0.15
12～16冊の累積相対度数は、１－0.15＝0.85〇
エ
（13）
全体は、６×６＝36通り
１～６を用いる２桁の整数で７の倍数は、【14、21、35、42、56、63】の６通り。
確率は、６/36＝１/６
（14）
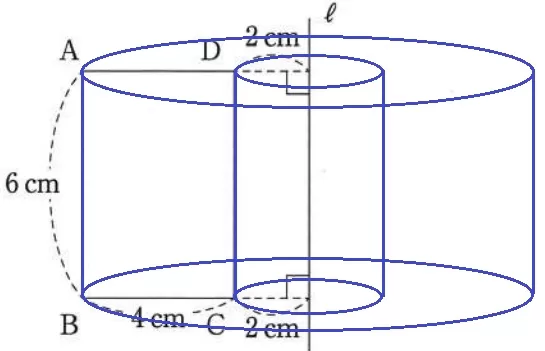
回転体はトイレットペーパーになる。
体積は、（６×６×π－２×２×π）×６＝192πｃｍ3
＠余談＠
回転体の体積には面白い定理がある。
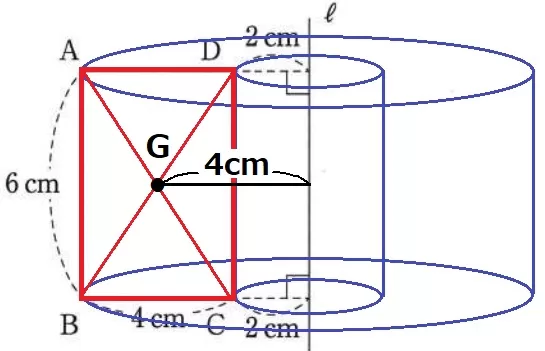
【パップス・ギュルダンの定理；回転体の体積＝断面積×重心の移動距離】
断面積は長方形ＡＢＣＤ。
その重心Ｇは対角線の交点で、軸との距離は４ｃｍである。
（４×６）×４×２×π＝192πｃｍ3
（15）
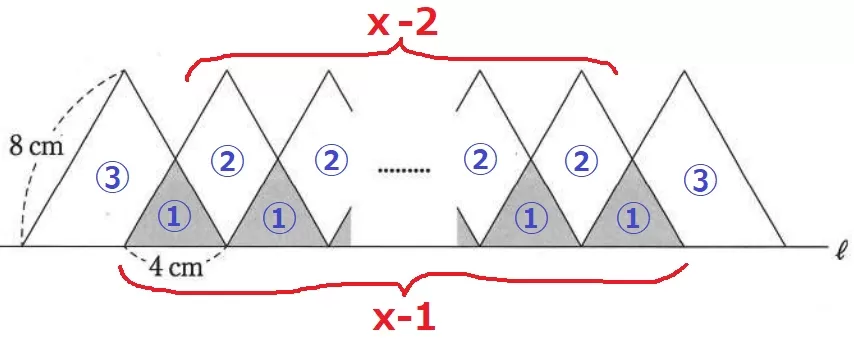
影１つの面積は正三角形の１/４。
影１つを①とすると、上図のようになる。
白…両サイドが③、あいだのｘ－２個が②→③×２＋②×（ｘ－２）＝２ｘ＋２
影…あいだのｘ－１個が①ずつ→ｘ－１
２ｘ＋２：ｘ－１＝５：２
内項と外項の積より、５（ｘ－１）＝２（２ｘ＋２）
５ｘ－５＝４ｘ＋４
ｘ＝９
（16）
最小値と最大値は同じなのに、期間①より期間②の方が開花日が早い理由を記述する。
端的に『第１四分位数（Q1）と第３四分位数（Q3）がともに期間②の方が早い』で良い。
箱の区間は全データの真ん中に集まる約50％で、全体的に期間②の方が早い。
大問２（平面図形）
（１）
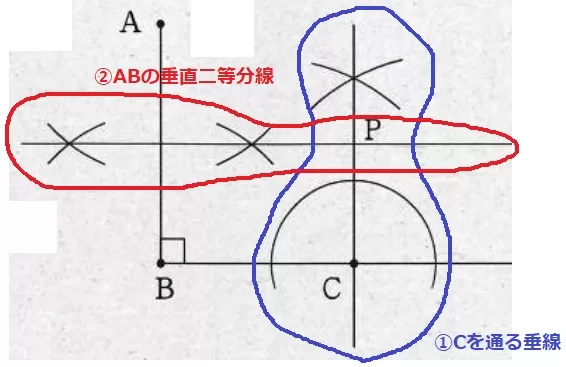
①ＡＢ//ＰＣ、∠ＡＢＣ＝90°から、ＰはＣを通る垂線上にある。
②ＡＢ：ＰＣ＝２：１から、ＰはＡＢの垂直二等分線上でもある。
①と②の交点がＰ。
（２）
△ＡＣＤ≡△ＡＧＢの証明。
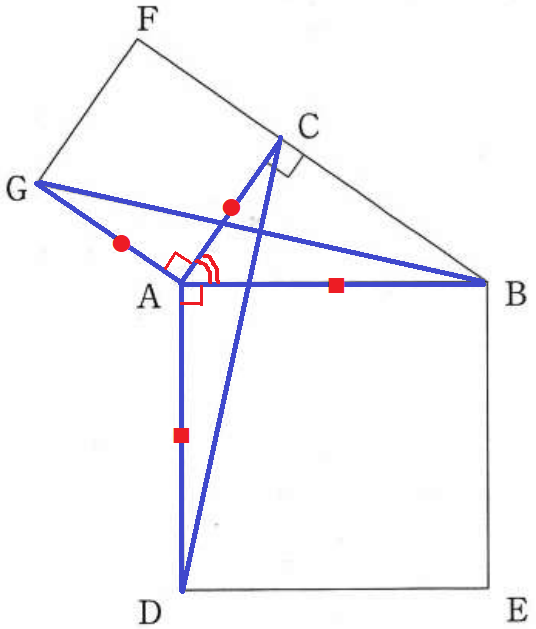
正方形の辺からＡＣ＝ＡＧ、ＡＤ＝ＡＢ
∠ＣＡＢ＝∠ＣＡＢ＋90°＝∠ＧＡＢ
２辺とあいだの角が等しいので合同。
大問３（関数）
（１）
ｙ＝ｘにｘ＝ｔを代入→Ｑのｙ座標はｔ
ｙ＝１/３ｘ2にｘ＝ｔを代入→Ｒのｙ座標は１/３ｔ2
ア…ｔ、イ…１/３ｔ2
（２）
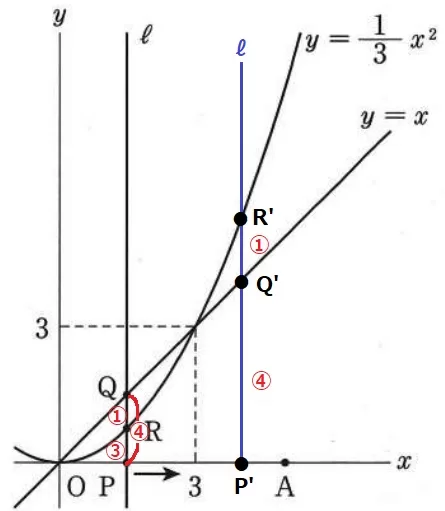
０＜ｔ＜３のときは上から順にＱ・Ｒ・Ｐだが、
３＜ｔ≦５のときはＲ・Ｑ・Ｐになる。
つまり、３を過ぎるとＱとＲが逆転してＰＲが最も長くなるので、
ＰＱ：ＰＲ＝４：３は成り立たない。
『Ｒのｙ座標がＱのｙ座標より大きくなるから』
（３）
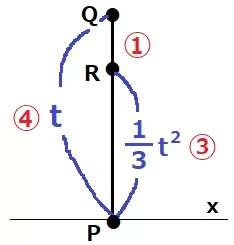
０＜ｔ＜３の場合、ｔ：１/３ｔ2＝４：３
内項と外項の積で、４/３ｔ2＝３ｔ
４ｔ2＝９ｔ
４ｔ2－９ｔ
＝ｔ（４ｔ－９）＝０
０＜ｔ＜３より、ｔ＝９/４
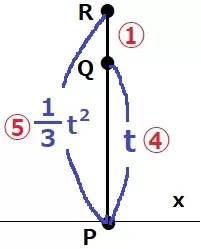
３＜ｔ≦５の場合、ｔ：１/３ｔ2＝４：５
内項と外項の積で、４/３ｔ2＝５ｔ
４ｔ2＝15ｔ
４ｔ2－15ｔ
ｔ（４ｔ－15）＝０
３＜ｔ≦５より、ｔ＝15/４
ｘ＝９/４、15/４
大問４（平面図形）
（１）
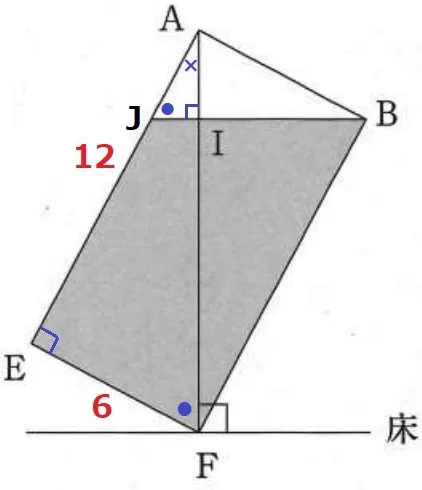
△ＡＥＦの内角において、∠ＡＦＥ＝●、∠ＦＡＥ＝×とする。
●＋×＝90°で、内角が●―×―90°であれば、ＡＥ：ＥＦ＝２：１の比が使える。
水面の左端をＪとする。
ＡＦ⊥ＪＢだから∠ＡＩＪ＝90°→△ＡＪＩにおいて、∠ＡＪＩ＝●
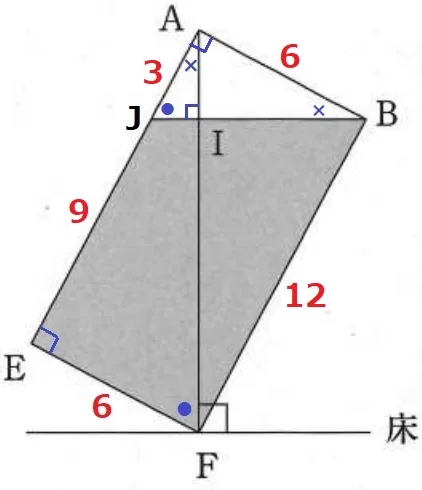
∠ＪＡＢ＝90°
△ＢＡＪは内角が●―×―90°なので、ＢＡ：ＡＪ＝２：１→ＡＪ＝６÷２＝３ｃｍ
ＥＪ＝12－３＝９ｃｍ
水の体積は、（９＋12）×６÷２×６＝378ｃｍ3
（２）
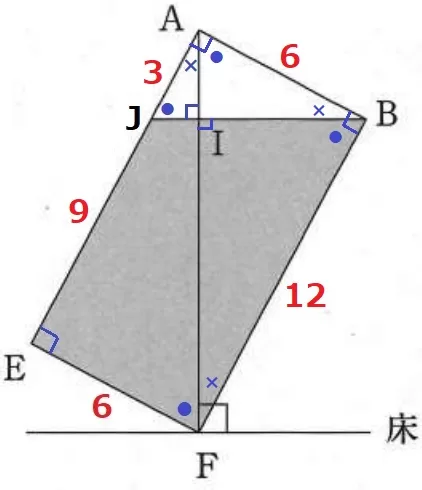
●×の角度調査を続ける。
∠ＡＢＦ＝90°だから∠ＩＢＦ＝●
求めたいＦＩを１辺とする△ＦＩＢも２：１が使える。
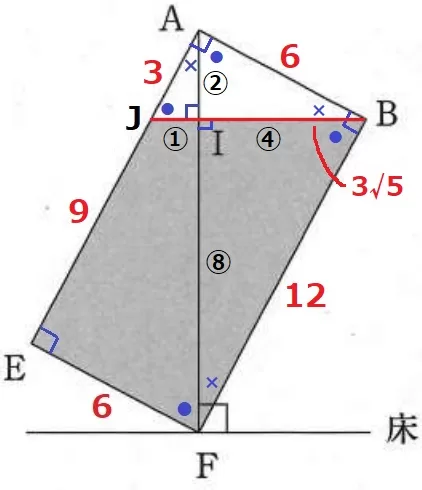
最も短いＪＩの長さを①とする。
△ＡＩＪの辺の比から、ＡＩ＝①×２＝②
△ＢＩＡで、ＢＩ＝②×２＝④
△ＦＩＢで、ＦＩ＝④×２＝⑧
△ＢＡＪで三平方→ＪＢ＝３√５ｃｍ
ＦＩ＝３√５×⑧/⑤＝24√５/５ｃｍ
大問１
ここだけで配点が65点！
（９）までは取る。36点get
（10）△ＡＥＨの内角は弧の長さの比で案分できる。
（11）外側延長で面積比を移していく。
隣辺比で△ＥＢＦの周りの３つの三角形を控除してもいい。
（12）終わりに近いので、余事象にように求める。
（15）差が出る。各々の面積比を出しておく。
影の部分は正三角形の－１個だが、あいだの白は－２個である点に注意。
（16）期間②の箱は期間①より左側にある。指定ワードをそのまま使う。
大問２
（１）先にどんな台形になるかイメージしよう。ＰはＣの真上、Ａの右側にある。
（２）問題集によくある形。Ａを中心に回転移動させると重なる。
大問３
（１）誘導に従う。
（２）ＰＱ：ＰＲ＝４：３はＰＱ＞ＰＲ。
３を超すとＱとＲの位置が変わり、ＰＱ＜ＰＲとなる。
（３）拡大図を書いて整理しておこう。内項外項の積で計算する。
大問４
（１）正面からみた図で、水の台形の面積を求める。
（２）辺の比が１：２の直角三角形を見つける。
２倍していくと、十字の部分をすべて比で表すことができる。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント