2024年度　高知県公立高校入試問題過去問【数学】解説

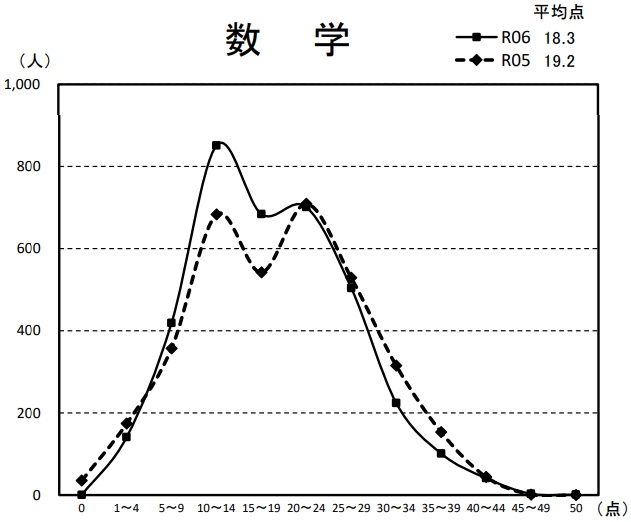
平均18.3点（前年比；－0.9点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　92.6％
－４＋（－６）－（－２）
＝－４－６＋２
＝－８

②　75.8％
（ｘ－ｙ）/２－（ｘ＋３ｙ）/５
＝｛５（ｘ－ｙ）－２（ｘ＋３ｙ）｝/10
＝（５ｘ－５ｙ－２ｘ－６ｙ）/10
＝（３ｘ－11ｙ）/10

③　66.7％
４ａｂ²÷（－６ａ³）×９ａ²ｂ
＝－６ｂ³

④　63.1％
√24÷√２－９/√27
＝√12－９/(３√３)
＝２√３－√３
＝√３

（２）　47.8％
ａ個のみかんを５ｂ個配ったら、余りは25個より多い。
ａ－５ｂ＞25
ア

（３）　31.3％！

歩いた距離が80ａｍ、走った距離が200ｂｍ、合計が1200ｍ。
80ａ＋200ｂ＝1200
200ｂ＝－80ａ＋1200　←÷200
ｂ＝－２/５ａ＋６

（４）　42.0％
ｘ²－８ｘ＋４＝０
解の公式を適用して、ｘ＝４±２√３

（５）　7.6％!!
一次関数ｙ＝－２ｘ－１の変化の割合→傾き－２
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（３＋９）＝－２
ａ＝－１/６

（６）　23.4％！

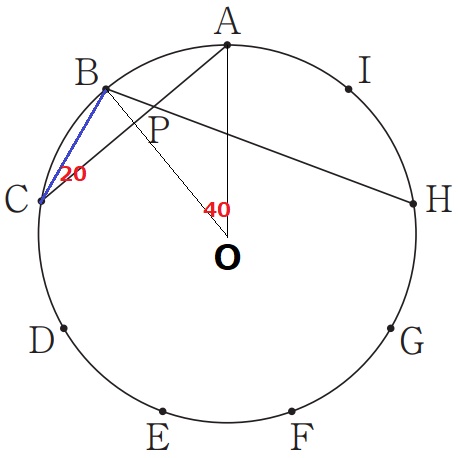
中心をＯとする。
弧ＡＢは円周の９分の１→弧ＡＢに対する中心角ＡＯＢ＝360÷９＝40°
弧ＡＢに対する円周角ＡＣＢ＝40÷２＝20°

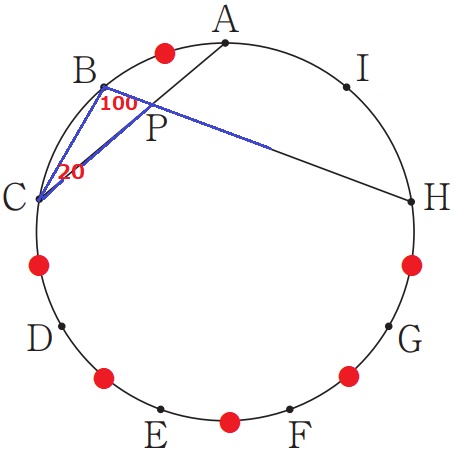
弧ＡＢ：弧ＣＨ＝∠ＡＣＢ：∠ＣＢＨ＝１：５
∠ＣＢＨ＝20×５＝100°
△ＢＣＰで外角定理→∠ＣＰＨ＝20＋100＝120°

（７）　41.5％
５枚から十の位・一の位と順番をつけて２枚とる→₅Ｐ₂＝20通り
３の倍数→12、15、21、24、42、45、51、54の８通り。
３の倍数でない確率は、１－８/20＝３/５

（８）出題ミスにより、受検者全員を正答扱い

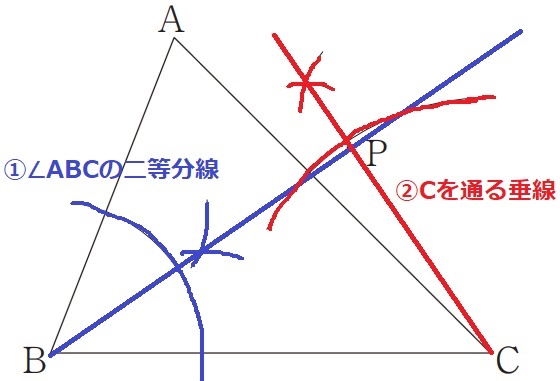
①２辺ＡＢ、ＢＣから等距離→∠ＡＢＣの二等分線
②Ｃから最短距離にある→Ｃを通る垂線。交点がＰ。

大問２（規則）

（１）　75.0％
左列は平方数が並ぶ。
６番目は６²＝36

（２）　15.5％！

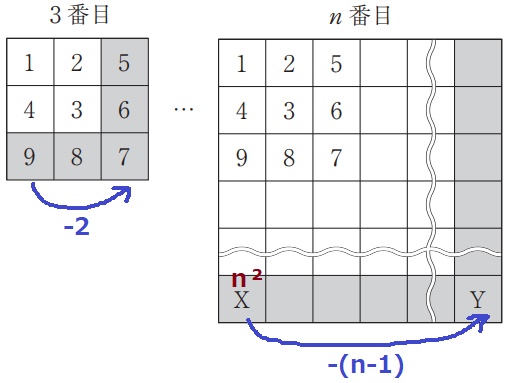
Ｘはｎ番目の平方数→ｎ²
ＸとＹの差→ｎ－１
Ｙの値は、ｎ²－（ｎ－１）＝ｎ²－ｎ＋１
ア…ｎ²、イ…ｎ－１、ウ…ｎ²－ｎ＋１

（３）　21.9％！
７²＝49、８²＝64
８番目のＬ字は50～64。個数は64－50＋１＝15個
等差数列の和の公式より、
（50＋64）×15÷２＝855

大問３（データの活用）

（１）　37.2％

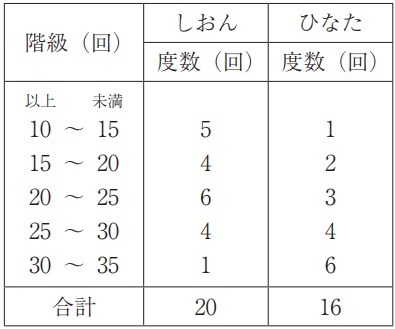
累積相対度数は、その階級までの相対度数の和。
（５＋４＋６）/20＝15/20＝３/４＝0.75

（２）　20.4％！
16個の第３四分位数は上位８個の真ん中、上から４番目と５番目の平均。
30～35回の階級の階級値である32.5回。

（３）　40.2％
ア：最頻値…最もあらわれている値。しおんでは20～25回の階級に含まれる。〇
イ：２人とも最小値は10～15回の階級に含まれるが、それ以上の詳細はわからない。×
ウ：20人の中央値は10番目と11番目の平均→20～25回の階級
16人の中央値は８番目と９番目の平均→25～30回の階級だから、しおんの方が小さい。〇

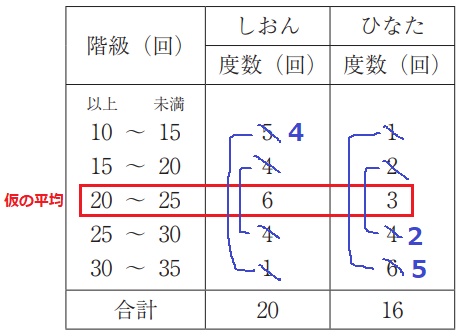
エ：度数分布表は各データの具体的な値はわからないが、
データに偏りがあれば平均値の大小関係がわかる場合もある。
しかし、本問は微妙である…。
１つのやり方としては、20～25の階級である階級値23.5を仮の平均として、
そこから等距離にある階級の度数を相殺していく。
すると、ひなたの方が平均値が大きくなりそうなので、しおんが大きいとは必ずしも言えない。×
ア・ウ

＠余談＠
しおんの平均値を大きく見積もると22回、ひなたの平均値を小さく見積もると23.75回。
ひなたの方が平均値は大きい。

大問４（数量変化）

（１）　5.1％!!

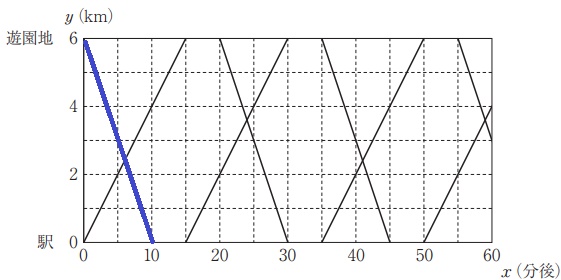
この直線の式を求める。
右に10、下に６だから、傾きは－６/10＝－３/５
切片は（０、６）
ｙ＝－３/５ｘ＋６

（２）　10.7％！

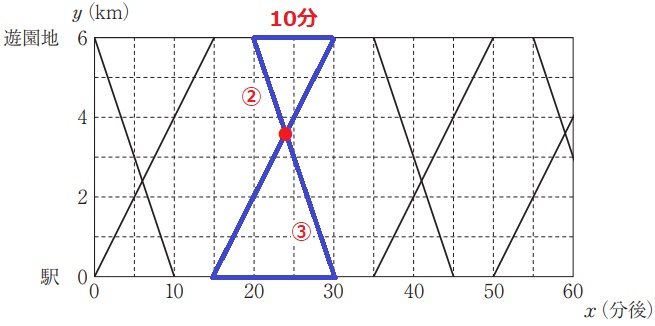
求めるべき交点は●。青線の∽を使う。
横線の時間をみると２マスと３マス→相似比は②：③
駅からの距離は、６×③/⑤＝3.6ｋｍ
時間は【10分＝⑤】なので、20＋10×②/⑤＝24分後
13時24分に、駅から3.6ｋｍの地点ですれ違う。

大問５（関数）

（１）　38.9％

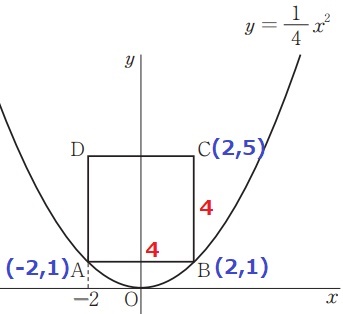
ｙ＝１/４ｘ²にｘ＝－２を代入→Ａ（－２、１）
Ｂはｙ軸についてＡと対称→Ｂ（２、１）
正方形の１辺であるＡＢ＝ＢＣ＝２－（－２）＝４
Ｂ座標から上に４→Ｃ（２、５）

（２）　3.3％!!

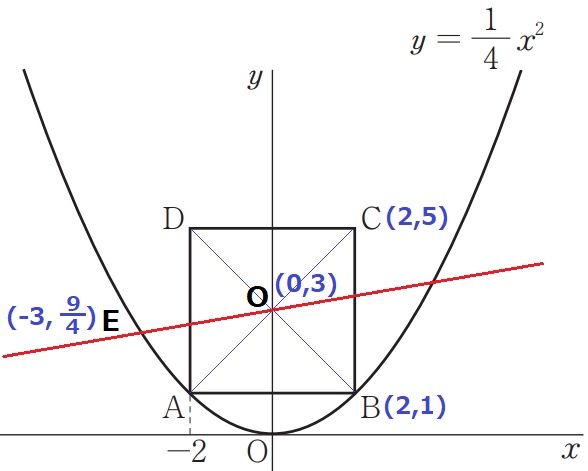
ｙ＝１/４ｘ²にｘ＝－３を代入→Ｅ（－３、９/４）
正方形の対角線はそれぞれの中心で交わり、その交点をOとする。
O（０、３）を通過する直線は正方形ＡＢＣＤを２等分する。
ＥＯを求めればいい。
Ｅ（－３、９/４）→Ｏ（０、３）
右に３、上に３－９/４＝３/４なので、傾きは３/４÷３＝１/４
切片はＯのｙ座標だから、ｙ＝１/４ｘ＋３

（３）　0.3％!!!

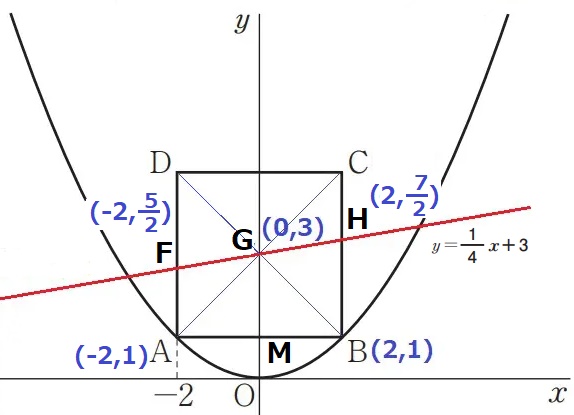
y=１/４ｘ＋３にｘ＝－２、２を代入→Ｆ（－２、５/２）Ｈ（２、７/２）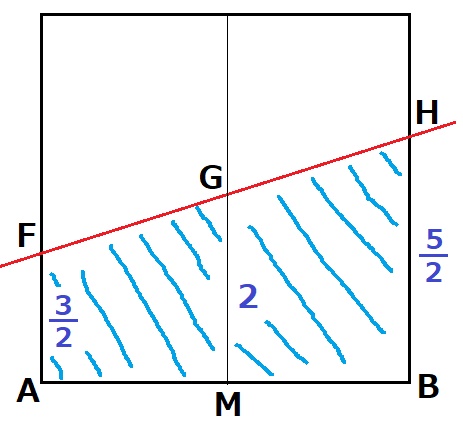
ＦＡ＝３/２、ＧＭ＝２、ＨＢ＝５/２
台形の面積比は上底と下底の和から求まる。
四角形ＡＭＧＦ：四角形ＭＢＨＧ
＝（３/２＋２）：（２＋５/２）
＝７/２：９/２
＝７：９

大問６（平面図形）

（１） 8.1%!!（部分点含む15.3％）
△ＡＢＤ≡△ＣＥＤの証明。

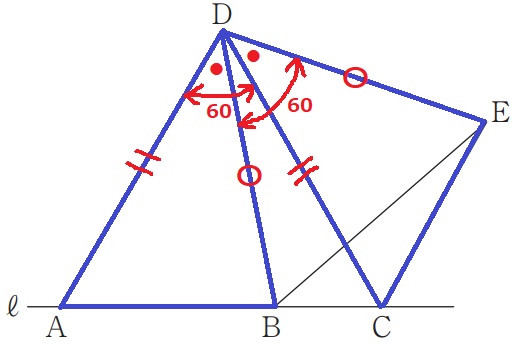
正三角形ＡＣＤより、ＤＡ＝ＤＣ
正三角形ＢＥＤより、ＤＢ＝ＤＥ
∠ＡＤＢ＝60－∠ＢＤＣ＝∠ＣＤＥ
２辺とあいだの角が等しいので合同。

（２） 1.5%!!

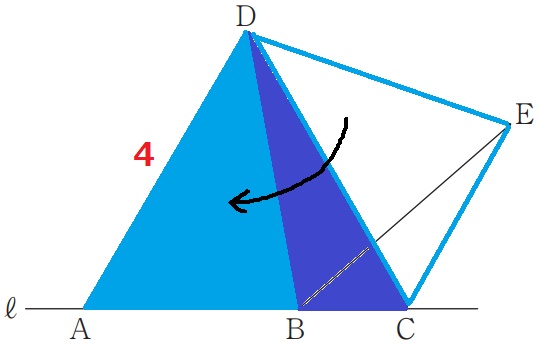
前問の合同から、△ＣＥＤを△ＡＢＤに移すと、
四角形ＢＣＥＤは△ＡＣＤに変形できる。
１辺４ｃｍの正三角形の高さは、４×√３/２＝２√３ｃｍ
４×２√３÷２＝４√３ｃｍ²
公立高校入試解説ページに戻る