2024年度　愛媛県公立高校入試問題過去問【数学】解説

平均27.7点（前年比；＋4.6点）

問題ＰＤＦ

大問１（計算）

（１）　98％
－３＋８
＝５

（２）　91％
（－９/２）÷（－３/４）
=６

（３）　85％
（－３ａ）²×２ａ
＝９ａ²×２ａ
＝18ａ³

（４）　80％
（√３＋１）²－９/√３
＝３＋２√３＋１－３√３
＝４－√３

（５）　81％
（ｘ＋４）（ｘ－４）＋（ｘ－５）（ｘ－１）
＝ｘ²－16＋（ｘ²－６ｘ＋５）
＝２ｘ²－６ｘ－11

大問２（小問集合）

（１）　77％
ｘ²－３ｘ－18
＝（ｘ＋３）（ｘ－６）

（２）　82％
確率なので、必ず何かが起こると断言はできない。
大数たいすうの法則…試行回数を増やしていくほど、ある事象が発生する割合が一定の値に近づいていく。
カードを取り出す回数を増やすと、確率は１/４に近づく。
ア

（３）　35％

上に凸のグラフのｃは負の数。下に凸のａ、ｂは正の数。
比例定数の絶対値が大きくなるほど、グラフの開きは小さくなる→ａ＜ｂ
ｃ＜ａ＜ｂ

（４）　53％
方陣算。

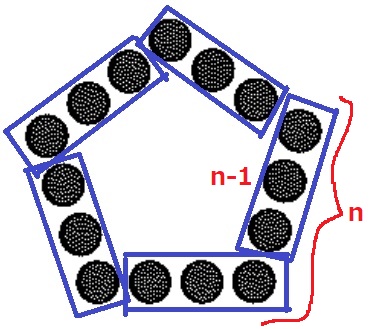
１辺をｎとすると、ｎ－１が５組あらわれる。
５（ｎ－１）＝５ｎ－５個

（５）　35％

60÷２＝30°
①ＢＣを１辺とする正三角形。
②角の二等分線。ＡＣとの交点がＰとなる。

（６）　49％

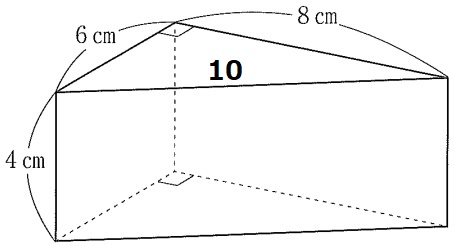
底面は３：４：５の直角三角形→斜辺は10ｃｍ
側面を広げると、縦４ｃｍ、横６＋８＋10＝24ｃｍの長方形。
表面積は、６×８÷２×２＋４×24＝144ｃｍ²

（７）　60％
答案では用いる文字が何かを示し、連立方程式を立てて過程も書く。
４人組をｘ組、５人組をｙ組とする。
組の合計で等式。
ｘ＋ｙ＝16　…①
人数の合計で等式。
４ｘ＋５ｙ＝73　…②

②－①×４をすると、ｙ＝７
①に代入、ｘ＝16－７＝９
４人組…７組、５人組…９組

大問３（総合問題）

（１）　67％
斜面に転がしたボールは等加速度運動をする。
ｙ＝ａｘ²に（ｘ、ｙ）＝（２、８）を代入。
８＝４ａ
ａ＝２
ｙ＝２ｘ²

（２）　61％
高さ1.5ｍ→影２ｍ
高さ□ｍ→影８ｍ
□＝1.5×８/２＝６

（３）　34％

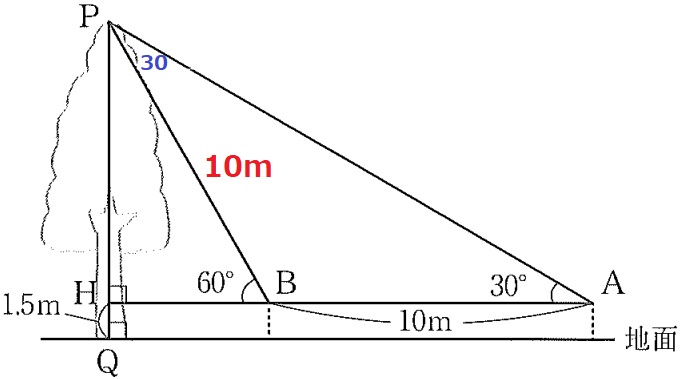
△ＡＢＰで外角定理→∠ＡＰＢ＝60－30＝30°
△ＡＢＰは２つの底角が等しいから二等辺三角形。
ＰＢ＝10ｍ
△ＰＢＨの辺の比は１：２：√３→ＰＨ＝10×√３/２＝５√３ｍ

（４）　７％!!

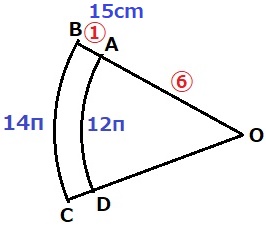
扇形ＯＡＤと扇形ＯＢＣは中心角が同じ。
→弧の長さの比＝円周の長さの比＝直径の比＝半径の比
（*円周の長さℓ＝２πｒだから、円周ℓの比は直径２ｒ、半径ｒの比と同じ）
ＢＯ：ＡＯ＝14π：12π＝⑦：⑥
→ＢＡ：ＡＯ＝①：⑥（①＝15ｃｍ）
求めたいのは内側の円の直径だから、15×⑥×２＝180ｃｍ

大問４（関数）

（１）　63％
ｙ＝ａｘ²においてｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１/４（４＋８）＝３

（２）　50％
ｙ＝１/４ｘ²にそれぞれのｘ座標を代入。
Ａ（－４、４）→Ｂ（８、16）
右に12、上に12だから、傾きは12/12＝１
Ａから右に４、上に４移動して、切片は４＋４＝８
ｙ＝ｘ＋８

＠余談＠
前問のように変化の割合（傾き）を求めると、
１/４｛（－４）＋８｝＝１

（３）①　27％！

Ｑはｙ＝ｘ＋８上の点→Ｑ（ｔ、ｔ＋８）
Ｓのｙ座標はＱと同じだから、ｔ＋８

②　３％!!
各座標を示すと上図のようになる。
四角形ＰＱＳＲが正方形→ＰＱ＝ＱＳ
ＰＱ＝（ｔ＋８）－１/４ｔ²＝－１/４ｔ²＋ｔ＋８
ＱＳ＝０－ｔ＝－ｔ

－１/４ｔ²＋ｔ＋８＝－ｔ
１/４ｔ²－２ｔ－８＝０　←４倍
ｔ²－８ｔ－32＝０
解の公式を適用。－４＜ｔ＜０だから、ｔ＝４－４√３

大問５（平面図形）

（１）①　30％！
△ＣＡＥ≡△ＣＤＢの証明。

正三角形ＣＡＤ→ＣＡ＝ＣＤ
正三角形ＢＣＥ→ＣＥ＝ＣＢ
∠ＡＣＥ＝60＋∠ＤＣＥ＝∠ＤＣＢ
２辺とあいだの角度が等しいから合同。

②　67％

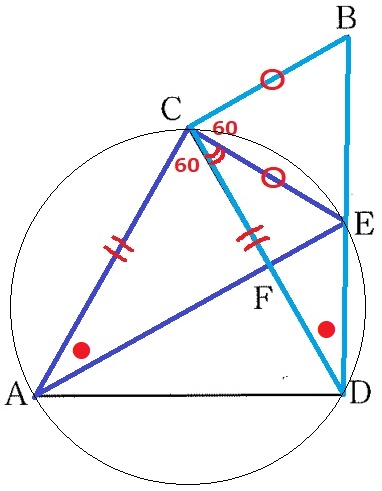
前問の合同から、対応する角で∠ＣＡＥ＝∠ＣＤＢ（●）
Ａ、Ｄが線分ＣＥについて同じ側にあり、∠ＣＡＥ＝∠ＣＤＥだから、
円周角の定理の逆より４点Ａ、Ｃ、Ｄ、Ｅは同一円周上にある。
ウ

（２）　11％！

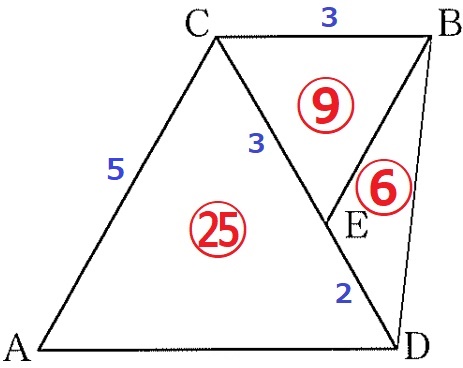
正三角形ＣＡＤ：正三角形ＢＣＥの相似比は５：３→面積比は２乗して㉕：⑨
ＥＤ＝ＣＤ－ＣＥ＝５－３＝２
ＣＥ：ＥＤ＝△ＢＣＥ：△ＢＥＤ＝３：２だから、
△ＢＥＤ＝⑨×２/３＝⑥
したがって、四角形ＡＤＢＣの面積は△ＢＥＤの㊵÷⑥＝20/３倍