平均22.4点(前年比;-1.8点)
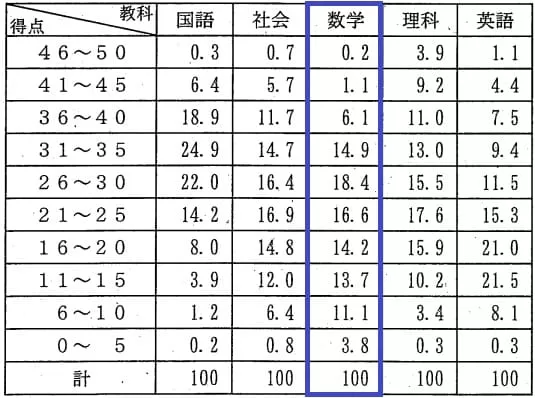
問題はこちら→リセマムさん
大問1(計算)
(1)① 99.3%
(-21)÷7
=-3
② 91.8%(部分正答0.5%)
-3/4+5/6
=1/12
③ 81.2%
(-3a)×(-2b)3
=-3a×(-8b3)
=24ab3
④ 89.7%(部分正答0.2%)
√8-√18
=2√2-3√2
=-√2
(2) 42.7%
【球の体積V=4/3πr3】
半径rの3乗がでてくる→球の体積比は半径の比の3乗。
半径を2倍すると、体積は23=8倍になる。
大問2(小問集合)
(1) 64.2%(部分正答1.1%)
31%⇒31/100
31/100amL
(2) 62.1%(部分正答0.7%)
3x+2y-4=0
2y=-3x+4
y=-3/2x+2
(3) 36.9%(部分正答3.0%)
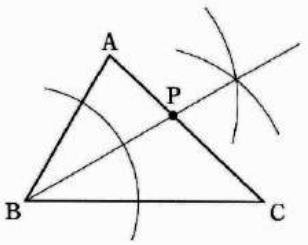
『辺AB、BCまでの距離が等しい』→∠ABCの二等分線を作図する。
ACとの交点がP。
(4) 69.3%
y=ax2において、xの値がp→qに増加したときの変化の割合はa(p+q)
1×(1+4)=5
(5) 33.0%!
最小値は2~4回→ア×
30人の中央値は15番目と16番目の平均で8~10回→イ×
第1四分位数は下位15人の真ん中、下から8番目で6~8回→ウ×
エ
大問3(確率・整数)
(1)① 81.2%(部分正答0.5%)
全体の取り出し方は、3×3=9通り
A>Bとなるのは、(2、1)(3、1)(3、2)の3通り。
確率は3/9=1/3
@別解@
ルール(ア)はAの玉を戻すから、数が等しい”あいこ”が起こる。
じゃんけんと同様で、勝ちか負けかあいこが同じ確率で起こる→1/3
② 50.4%(部分正答8.5%)
前問より、ルール(ア)でAが景品をもらえない確率は1-1/3=2/3
ルール(イ)でAが景品をもらえない確率を計算する。
全体は、3×2=6通り
A<Bとなるのは、(1、2)(1、3)(2、3)の3通り。
確率は3/6=1/2
2/3>1/2だから、ルール(ア)の方がAが景品をもらえない確率が大きい。
ルール…ア、確率…2/3
@余談@
ルール(イ)はあいこが起こらないので、結果は勝ちか負けの1/2。
あいこでは景品をもらえないため、あいこの可能性を含むルール(ア)の方がもらえにくい。
(2)① 66.8%
「常に同じになる」とあるので、左上の4マスで試せば良い。
a=1、b=2、c=8、d=9
ad-bc
=1×9-2×8
=-7
② 5.5%!!(部分正答14.9%)
答案では理由も説明する。
nは1段に並べる整数の個数→1個下の数は+nになる。
b、c、dをa、nで表すと、
b=a+1、c=a+n、d=a+n+1
ad-bc
=a(a+n+1)-(a+1)(a+n)
=a2+an+a-a2-an-a-n
=-n
大問4(方程式)
49.8%(部分正答24.6%)
4人グループをx組、5人グループをy組とする。
生徒の合計で等式。
4x+5y=200 …①
配ったゴミ袋の数で等式。
生徒1人に1枚ずつ配るので200枚は必ず配る。
これにグループごとの予備の枚数を加える。
200+2x+3y=314
2x+3y=114 …②
①、②の連立を解くと、x=15、y=28
4人グループ…15組、5人グループ…28組
大問5(平面図形)
(1) 30.7%!(部分正答22.0%)
△EDO∽△EBDの証明。
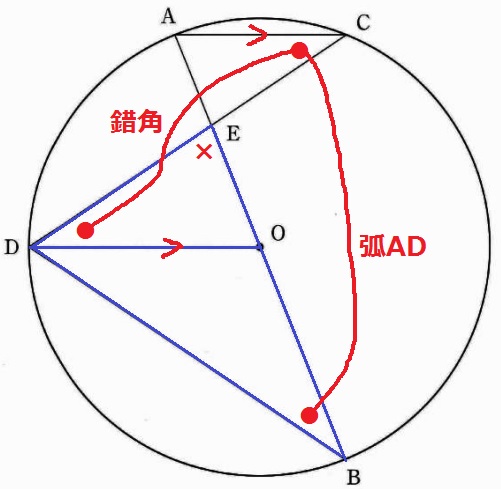
共通角(×)、AC//DOの錯角と弧ADに対する円周角(●)
2角相等で∽。
(2) 2.1%!!(部分正答0.5%)
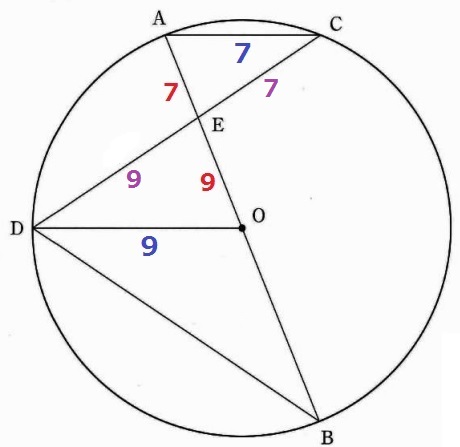
△EDO∽△ECAの相似比は9:7。
△EDO∽△EBDの相似比を求めるには対応する辺の比が欲しいが、
なかなか出てこない…(´д`)
面積比から攻めてみる。
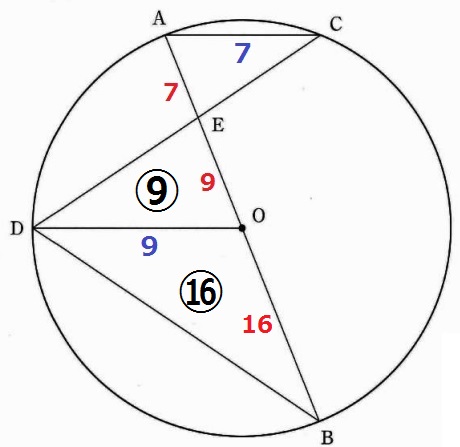
B側の情報を得るために、円の半径を使う。
OB=OA=16
△EDO:△EBD=EO:EB=9:(9+16)=⑨:㉕
よって、相似比は△EDO:△EBD=3:5
大問6(関数)
(1) 53.4%
y=1/x、y=xにx=2を代入すると、
Bのy座標は1/2、Cのy座標は2。
BC=2-1/2=3/2
(2) 22.2%!
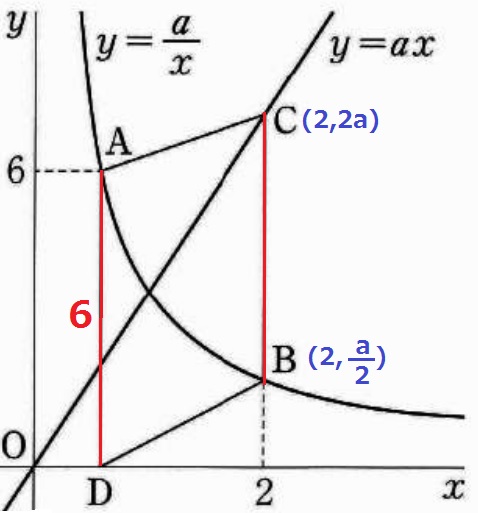
四角形ADBCが平行四辺形になるとき、対辺が等しくなる。
AD=CB=6
BとCのy座標をaで表すと上図になる。
CB=2a-a/2=3/2a=6
a=4
(3) 3.7%!!

a=1のときの四角形ADBCの面積を求める。
(1)よりBC=3/2、Aのx座標は1/6なので、
(6+3/2)×(2-1/6)÷2=55/8

四角形ADBCの面積をaで表す。
BC=3/2a、高さは2-a/6、面積は55/8だから、
1/2(6+3/2a)(2-a/6)
=1/2(12-a+3a-a2/4)
=-a2/8+a+6=55/8 ←両辺を8倍して整理
a2-8a+7
=(a-1)(a-7)=0
0<a<12なので、a=7
@余談@
a=4のとき、四角形ADBCは平行四辺形であった。
-a2/8+a+6にa=4を代入すると面積は8である。
他のaを計算してみると、
a=3、5は63/8で等積。
a=2、6は15/2で等積。
a=1、7は55/8で等積であった。
0<a<12でa=0だとグラフが無くなってしまうが、
a=0、8では値が6で等しくなり、
a=-1、9では値が39/8で等しくなる…。
すなわち、平均が4(和が8)となる組み合わせで等積になる。
試しに、-a2/8+a+6のaを(8-a)に置き換えてみると、
-(8-a)2/8+(8-a)+6
=-a2/8+a+6…と同じ値が出てくる|-`)
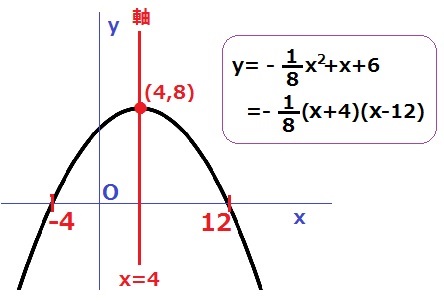
この理由なのですが、高校で習う2次関数を使います。
先ほどのaを変数xに置き換え、四角形ADBCの面積をyとし、
xの値を変えていくと、四角形ADBCの面積がどのように変化するかをグラフで表します。
y=-1/8x2+x+6
=-1/8(x2-8x-48)
=-1/8(x+4)(x-12)=0
x=-4、12のとき、面積yが0になる。
→グラフはx軸と(-4、0)(12、0)で交わる。
問題文で『0<a<12』とあるのは、a=12で面積が0になるからです。
放物線は左右対称で、対称軸を軸といいます。
a<0から上に凸のグラフ、軸の方程式は-4と12の真ん中のx=4
代入するとy=8だから、頂点の座標は(4、8)
つまり、x=4のとき、四角形ADBCの面積は8で最大になります。
そして、対称性から頂点から等距離にあるx座標の組み合わせは、
yの値が等しいので面積が等しいことになります。
(たとえば、x=3.9と4.1をあてはめると、いずれも面積は7.99875で等積になる)
ちなみに、頂点の座標は平方完成でも求めることができます。
y=a(x-p)2+qの標準形に変形すると、頂点の座標は(p、q)
y=-1/8x2+x+6
=-1/8(x2-8x)+6
=-1/8(x-4)2+8 →頂点(4、8)
大問7(空間図形)
(1) 52.3%
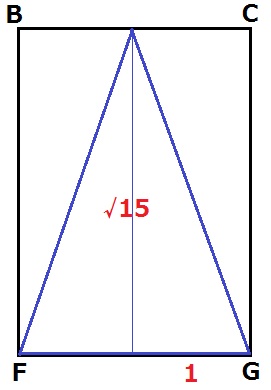
正面からみると、円錐は二等辺三角形。
三平方の定理より、円錐の母線は4cm。
(2) 19.0%!(部分正答0.2%)
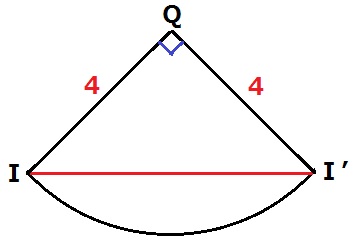
最短距離なので、展開図を作成する。
側面の扇形の中心角は、360×半径/母線=360×1/4=90°
ヒモを展開図に描くと上図のII’になる。
△OII’は直角二等辺三角形で辺の比は1:1:√2だから、
II’=4√2cm
(3) 2.8%!!

四角錐P―ABCDの高さが知りたい。まずはPの位置を確認する。
四角錐P―ABCDの体積が最小となる⇒Pは面ABCDに最も近い場所。
前問の展開図がヒントになる。
立体図でPは面EFGH上にあるIから最も遠くにあり、展開図でいえばPはII’の中点である。
直角三角形QIPより、QP=4×1/√2=2√2cm

Pから面ABCDに垂線をひき、足をRとする。
PRが求めるべき四角錐の高さにあたる。
正面から見た図で△QPR∽△QGCより、RP=√15×2√2/4=√30/2cm
よって、四角錐P―ABCDの体積は、2×2×√30/2÷3=2√30/3cm3
●講評●
6(3)と7(3)は時間を要する。
高得点を狙うには時間配分に注意したい。
大問1
ここだけで全体の5分の1にあたる配点がある。
大問2
(5)箱ひげ図も判断しやすかった。
ここもすべて取っておきたい。
大問3
(1)じゃんけんに置き換えると捉えやすかった。
(2)①で試行して②で証明する。
nをどう使うか。4つの整数の下段でnを用いる。
大問4
練習問題に良い。
袋の枚数は6x+8y=314でも解けるが、
〔1人ずつに配る200枚〕と〔グループごとの予備の袋〕に分けると少し楽。
大問5
(2)円が出てきたら半径を見る癖をつけたい。
大問6
(2)AD=6は固定。CBの長さをaで表す。
(3)やり方は文字に置き換えて方程式を立てるという高校受験の王道だが、
処理がやや複雑で時間を要する。後回しで良い。
大問7
(2)円錐の側面積である扇形の中心角や面積はすばやく出せるようにしたい。
(3)まずはPの位置をおさえること!
立体図からIから最も遠い場所→扇形の展開図でIから遠いのはQの真下。
立体の立面図から相似で高さを算出する。



コメント