平均50.3点（前年比；－9.6点）
問題はコチラ→ＰＤＦファイル
Ａ問題の解説はコチラ。
大問１（小問集合）
（１）
（√２－１）2－√50＋14/√２
＝２－２√２＋１－５√２＋７√２
＝３
（２）
Ａ問題の（５）
３ａ+４ｂ＜3000
*『より』なので3000円は含まない。
（３）
（ｘ+ｙ）2+７（ｘ＋ｙ）＋12 ←（ｘ＋ｙ）をＸに置き換える
＝Ｘ2＋７Ｘ＋12
＝（Ｘ＋３）（Ｘ＋４） ←Ｘを（ｘ＋ｙ）に戻す
＝（ｘ＋ｙ＋３）（ｘ＋ｙ＋４）
（４）
（ｘ－２）（ｘ＋３）＝－２ｘ
ｘ2＋３ｘ－６＝０
因数分解ができないので解の公式を適用。
ｘ＝（－３±√33）/２
（５）
無作為に抽出した20個のうち、白：赤＝４個：16個＝１：４
この割合は母集団も変わらないものとみなす。
白は100個だから、赤は400個。
（６）
【2020＝２×２×５×101】
2020/ｎが偶数となるには、素因数２を１つ残さなくてはならない。
残りの【２or５or101】はあってもなくてもいい。
２があるかないか、５があるかないか、101があるかないか→２×２×２＝８個
*具体的にいうと、ｎ＝１、２、５、101、２×５、２×101、５×101、２×５×101
ｎ＝１が抜けやすいと思われる。2020÷１＝2020で偶数。
（７）
Ａ問題の（８）
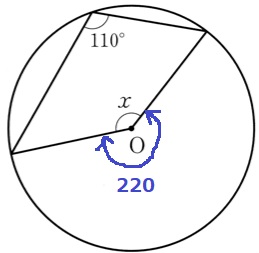
中心角はｘの下。
ｘ＝360－220＝140°
（８）
円の中心は２点の垂直二等分線上にある！
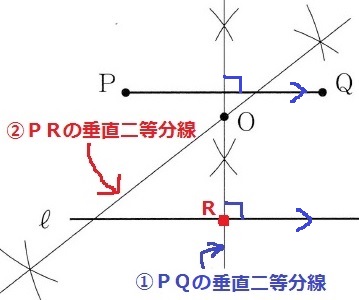
①ＰＱの垂直二等分線。この線上に中心Ｏがある。
ℓとの交点をＲとすると、円はＲで接する。
（半径ＯＲは接点Ｒでℓと直交するところ、平行線→同位角で90°）
②Ｒも円周上の点。ＰＲで垂直二等分線。交点がＯとなる。
（ＱＲの垂直二等分線でもＯＫ）
大問２（小問集合２）
（１）①
同じ目が出るパターンは（１、１）～（６、６）の６通り。
６/36＝１/６
②ア
２点以上が同じ点にあると３点にならないから三角形にならない。
（Ａ、Ａ）（Ｂ、Ｂ）（Ｃ、Ｃ）（Ｄ、Ｄ）（Ｅ、Ｅ）（Ｆ、Ｆ）→６通り
（Ａ、□）で□がＢ～Ｆで５通り、さらに（□、Ａ）の逆パターンで５通り。
計16通り。
16/36＝４/９
イ
正六角形の６つの頂点は同一円周上を通る。
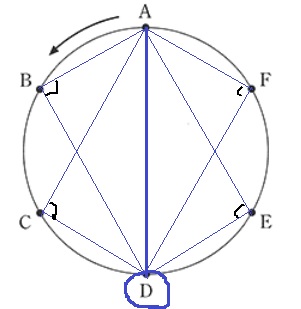
半円の弧に対する円周角は直角。
（Ｂ、Ｄ）（Ｃ、Ｄ）（Ｄ、Ｅ）（Ｄ、Ｆ）
これらの逆を含めて８通り。
今度はＡに直角を集める。
（Ｂ、Ｅ）（Ｃ、Ｆ）これらの逆を含めて４通り。
計12通り。
12/36＝１/３
2019年度千葉後期・大問２（４）で類題が出ています。
（２）①
Ａ問題と同じ。
80/500＝16/100＝0.16
*相対度数は小数で表す。
②最頻値（モード）が120円だから。
*モードは最もあらわれている値。
120円のおにぎりが最も売れている。
（３）
ここもＡ問題と同じ。
小さい奇数を２ｎ－１とおくと、大きい奇数は２ｎ＋１となる。
（２ｎ＋１）2－（２ｎ－１）2 ←平方の差
＝（２ｎ＋１＋２ｎ－１）（２ｎ＋１－２ｎ＋１）
＝４ｎ×２＝８ｎ
ｎは整数だから８ｎは８の倍数。
したがって、２つの続いた奇数では、
大きい奇数の平方から小さい奇数の平方を引いた差は８の倍数となる。
*最後のシメも忘れずに！
大問３（関数）
（１）
ｙ＝ｘ2に代入して、Ａ（２、４）Ｂ（－１、１）
Ｂ→Ａの座標移動で右に３、上に３だから、傾きは１。
Ｂから右に１、上に１移動して切片は２。
ｙ＝ｘ＋２
（２）
Ａ問題（３）と一緒。
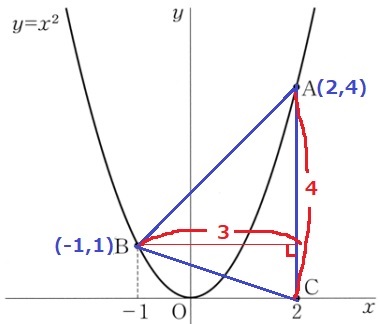
座標を確定できればいけるかと。
４×３÷２＝６
（３）①
△ＯＰＱは直角二等辺で、ｙ軸に対して左右対称。
ＰＱとｘ軸は平行。角度を調べていくと、ＯＰは赤い正方形の対角線。
45度線→傾きが－１→ＯＰ；ｙ＝－ｘ
Ｐはｙ＝－１/２ｘ2とｙ＝－ｘの交点。
－１/２ｘ2＝－ｘ
ｘ2＝２ｘ
ｘ2－２ｘ
＝ｘ（ｘ－２）＝０
Ｐのｘ座標は正なのでｘ＞０より、ｘ＝２
ｙ＝－１/２×２2＝－２
Ｐ（２、－２）
②
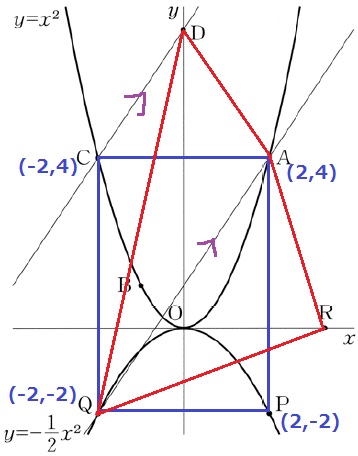
座標を確認すると、四角形ＡＣＱＰは長方形。
これと四角形ＡＤＱＲの面積が等しい。
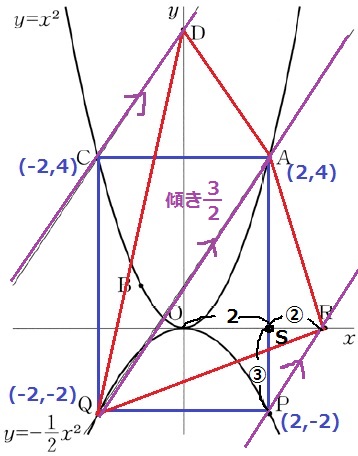
ポイントはＡＱで分割すること。
ＣＤ//ＱＡから等積変形で△ＡＣＱと△ＡＤＱの面積が一緒。
ということは、残りの△ＡＰＱと△ＡＲＱの面積が等しくなるので、
等面変形が成り立ち、ＱＡ//ＰＲとなる。
Ｑ→Ａは右に４、上に６だから、ＱＡの傾きは６/４＝３/２
平行よりＰＲの傾きも３/２
ＡＰとｘ軸との交点をＳとする。
ＰＲの傾きから、ＳＲ＝②、ＳＰ＝③（＝２）
ＳＲ＝２×②/③＝４/３
Ｒのｘ座標は、２＋４/３＝10/３
大問４（空間図形）
すべてＡ問題と同様。
（１）
正四面体の展開図。
③
（２）
底面積×高さ÷３
６×６×３√６÷３＝36√６ｃｍ3
（３）
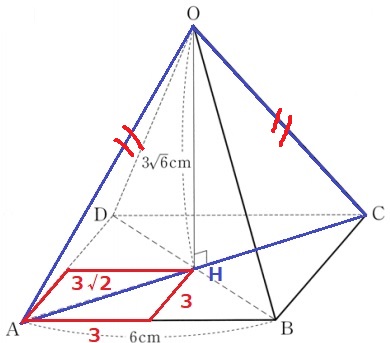
『正四面体ＯＡＢＣＤ』だからＯＡ＝ＯＣは確定。
ＡＣの長さはＯＡ・ＯＣに等しいか。
Ｏの足をＨとする。
赤い正方形は１辺３ｃｍの正方形で、ＡＨ＝３√２
もし、△ＡＯＣが正三角形であれば、∠ＡＯＨ＝30°でなければならない。
すなわち、△ＡＯＨの内角は30°－60°－90°の直角三角形となり、
辺の比は１：２：√３でＡＨ：ＨＯ＝１：√３となる。
ＡＨ：ＨＯ＝３√２：３√６＝１：√３
よって、△ＯＡＣは正三角形。（④）
（４）①
前問の解答を利用する。
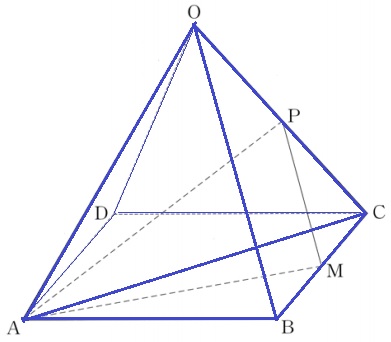
（２）より、正四角錘Ｏ－ＡＢＣＤの体積は36√６ｃｍ3であった。
三角錐Ｏ－ＡＢＣは底面が半分だから体積も半分。
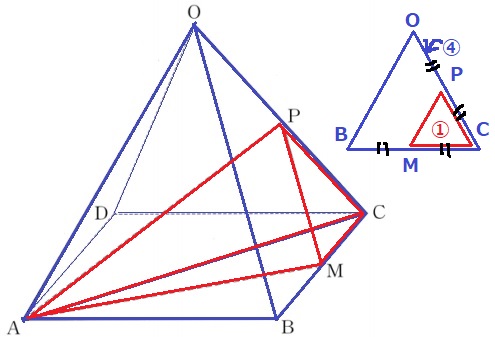
三角錐Ｏ－ＡＢＣを今度は△ＯＢＣを底面として捉える。
△ＯＢＣ：△ＰＭＣの面積比は４：１なので、
三角錐Ａ－ＯＢＣと三角錘Ａ－ＰＭＣの体積比も４：１。
したがって、三角錐Ａ－ＰＭＣの体積は、36√６×１/２×１/４＝９√６/２ｃｍ3
②
体積がわかったので、底面となる△ＡＰＣの面積を求めたい。
正三角形ＯＡＣに注目。
ＡＨ＝３√２ｃｍだったので、ＡＣ＝６√２ｃｍ
ＯＰ：ＰＣ＝１：１で、△ＯＡＣと△ＰＡＣの高さの比は２：１
→△ＰＡＣの面積は正三角形ＯＡＣの半分。
△ＰＡＣ…６√２×３√６÷２÷２＝９√３ｃｍ2
したがって、９√６/２×３÷９√３＝３√２/２ｃｍ
大問５（平面図形）
（１）①
ＢＥ＝ＡＢ－ＡＥ＝８－ｘｃｍ
②
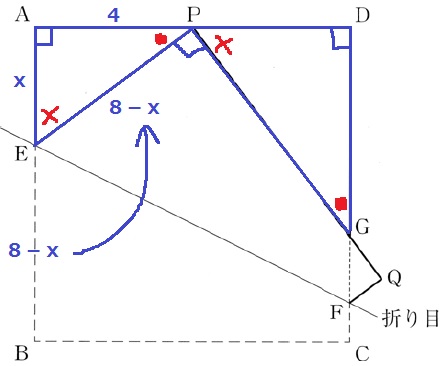
△ＡＥＰで三平方。
ｘ2＋４2＝（８－ｘ）2
ｘ2＋16＝64－16ｘ＋ｘ2
16ｘ＝48
ｘ＝３
（２）
△ＡＰＥ∽△ＤＧＰの証明。
方針は思いつきやすい。●＋×＝90°で調査して２角が等しい→∽
あとはきちんと記述できるかどうか。
（３）
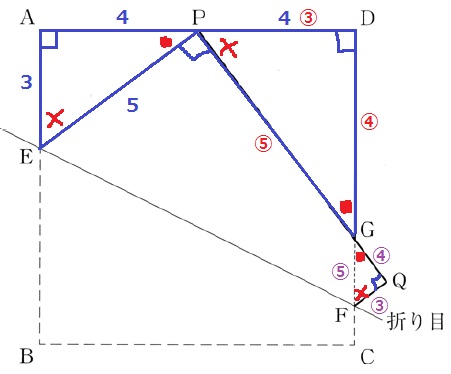
△ＱＧＦの内角も●－×－90°で、△ＱＧＦも相似。
△ＡＰＥの辺の比が３：４：５だから、△ＤＧＰも△ＱＧＦも辺の比は３：４：５。
ＰＧ＝４×⑤/③＝20/３
ＧＱ＝８－20/３＝４/３
ＦＱ＝４/３×③/④＝１ｃｍ
（４）
ＦＣ＝ＦＱ＝１ｃｍ
ＦＣを底辺としたときの△ＣＦＱの高さがわかればいい。
△ＣＦＱ付近をピックアップ。
ＱからＧＣに向けて垂線をひき、交点をＨとする。
△ＧＨＱと△ＱＨＦの内角を調べると●－×－90°…
すべて同じ相似図形で辺の比は３：４：５！
△ＱＨＦより、ＱＨ＝１×④/⑤＝４/５ｃｍ
△ＣＦＱの面積は、１×４/５÷２＝２/５ｃｍ2
大問６（数量変化）
すべてＡ問題と同じ。
（１）
昇の休憩は４～６分後→２分間
（２）
桜は2000ｍを一定の速さで16分間走る。
2000÷16＝分速125ｍ
（３）
６分後に注目。
昇は800ｍ地点で休憩をしている。
桜は125×６＝750m地点を走っている。
両者の差は800－750＝50ｍ
ここから昇は分速100ｍ、桜は分速125ｍで走るので１分間に25ｍずつ差が縮まる。
50÷25＝２分
よって、桜が昇に追いつくのは６＋２＝８分後
（４）①
千代のグラフを記入する。
千代は反対方向に走るので右下のライン。
分速100ｍだから400ｍを４分で走る。（４分後ごとに右下ライン）
交点の★がハイタッチする地点。
昇の４分後は下上に交点ができるがダブルカウントしないこと！
16回
②
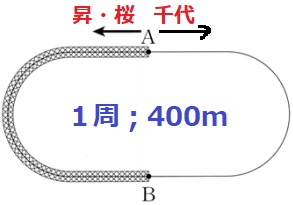
ＡＢは昇＆桜が出発する方向の半周にあたる。
ということは、先ほどのグラフの下半分がＡＢの区間に相当する。
★の数は９回。（昇の４分後は下でカウントすること！）
Ａ問題とそこそこ内容がかぶっている。
大問１
（６）正答率が悪そう。ｎ＝１を抜かさないように！
他は全部とりたい。
大問２
（１）②イ千葉では３人に１人しか正解者がいなかった。
円周角定理を使って過不足なくパターンを見つける。
大問３
（２）②問題文でわざわざＡＱに焦点をあてているので、
長方形ＡＣＱＰを対角線ＡＱの左上と右下に分ける発想に飛ばしたい。
大問４
Ａ問題に同じ。（３）二等辺じゃないよ！
（４）②空間図形は視点をうまく切り替える。
大問５
問題集でよくあるパターン。
特色があったのは（４）。△ＣＦＱの高さとなる線分を１辺とする三角形の∽を探る。
大問６
Ａに同じ。情報整理ができれば計算処理は少なかった。
公立高校入試解説ページに戻る
コメント