2018年度　栃木県公立高校入試【数学】解説

記述式が５題。
基本～標準問題が多いです。
最後の正方形はぬかりなく調査できるかどうか。
問題はコチラから→ＰＤＦファイル

大問１（計算）

（１）　98.7％
（－１２）÷３＝－４

（２）　85.8％
１/４xy³×８ｙ＝２xy⁴

（３）　93.4％
√２＋√１８
＝√２＋３√２
＝４√２

（４）　92.7％
（ｘ＋4）²
＝ｘ²＋８ｘ＋１６

（５）　81.5％
５ａ＋２ｂ＝７ｃ
５ａ＝－２ｂ＋７ｃ
ａ＝（－２ｂ＋７ｃ）/５

（６）　77.5％
不等式で表す。「より軽い」→未満。
６ｘ＋7＜900

（７）　80.9％
内項と外項の積は一緒。
５：（9－ｘ）＝２：３
２（９－ｘ）＝５×３
１８－２ｘ＝１５
２ｘ＝３
ｘ＝３/２

（８）　70.9％
錘の体積：底面積×高さ×１/３
５π×７×１/３＝３５/３πｃｍ³

（９）　85.1％
連立方程式
代入法でも加減法でもＯＫ。
ｘ＝２　ｙ＝－３

（１０）　79.9％
ｘ²－６ｘ－７＝０
（ｘ－７）（ｘ＋１）＝０
ｘ＝－１、７

（１１）　58.5％
１つの内角が１５０°ということは、その外角は３０°
多角形の外角の和は常に３６０°で、
本問は正多角形だから、どの外角も３０°
よって、３６０÷３０＝１２　→　正十二多角形

（１２）　94.3％
３本目の平行線をひく。

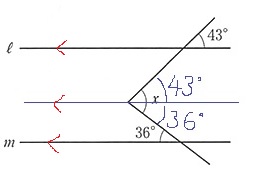
同位角と錯角を駆使して、、
ｘ＝４３＋３６＝７９°

（１３）　71.0％
最も度数が多い階級＝モード
モードは130～150の階級で１２人。
１２/４０＝3/10＝０．３

（１４）　63.5％
傾き＝（ｙの増加量）/（ｘの増加量）
ｙ＝{－４²－（－１²）}/（４－１）＝－１５/３＝－５

大問２（小問集合）

（１）作図　43.7％
Ａから最も遠い円周上のＰ→Ａを通る直径でＡ側にない円周上の点。
適当な垂直二等分線の交点から円の中心点を求めてもよいし、
公式解答のようにＡから円周にむけてピョコピョコ→２つの交点の二等分線でもＯＫ

（２）確率　56.5％
素数は組み合わせは、
（１．３）（２．３）（３．１）（４．１）（４．３）の５通り
（*１１も素数だけど、１は２回選べない！）
２枚選ぶ組み合わせは、４×３＝１２通り
よって、５/１２

（３）関数　50.4％
Ｂのｘ座標は２。ｙ＝－５/４ｘへ放り込み。
ｙ＝－５/４・２＝－５/２
Ｂのｙ座標が－５/２。
Ａのｙ座標は、
６－│－５/２│　　←距離なので絶対値計算
＝６－５/２＝７/２
Ａ（２、７/２）
これをｙ＝ａ/ｘへ代入。
７/２＝ａ/２　　ａ＝７

大問３（式の証明）

記述式解答。詳細は公式解答にて。
（１）整数の証明。　18.2％！　部分正答含－40.2％
５円硬貨の枚数をｂとして、等式をたてる。
４倍の証明なので、最終形態は４（　～～～　）の形。
（　～～～　）内が整数である指摘して、４（　～～～ ）が４の倍数と示す。

（２）２次方程式　28.6％！　部分正答含－61.6％
等式を立てて解く。長さはｘ＞０なので、ｘ＝３となる。

大問４（平面図形）

（１）合同図形の証明　42.6％　部分正答含－88.7％
等しい辺・角度に記号をふる。
二等辺三角形の底角が等しいので、
ここから１辺とその間の角が等しいことを指摘する。

（２）①　20.6％！
都立の大問４にも似たような設問がある。
∠ＡＣＢは直径ＡＢに対する円周角で９０°
∠ＡＤＯ＝∠ＡＣＢ＝９０°
同位角が等しいので、ＤＯ//ＣＢ
同位角から∠ＥＯＤ＝∠ＯＢＣとなるので、
∠ＥＯＤをａで表せればいい。
△ＯＥＤは半径からＯＥ＝ＯＤの二等辺三角形で、
∠ＯＤＥ＝ａ
∠ＥＯＤ＝180－２ａ　　よって、∠ＯＢＣ＝180－２ａ°

②　18.7％！
ドーナッツ型の面積を求める。
外側と内側の円の半径が知りたいところ。
外側の半径は、△ＡＣＢが直角三角形なので三平方から、
ＡＢ＝√（１２²＋４²）＝√１６０＝４√１０
よって、外側の半径は２√１０ｃｍ
内側の円の半径はＤＯ。
前問の通り、ＤＯ//ＣＢ→２角の等しさから△ＡＤＯ∽△ＡＣＢ
ＡＯ：ＡＢ＝１：２なので、ＤＯ：ＣＢ＝１：２
ＤＯ＝２ｃｍ
ドーナッツの面積は、
２√１０×２√１０×π－２×２×π
＝４０π－４π＝３６πｃｍ²

大問５（数量変化）

的確に情報整理！
Ｐ；Ａ→Ｂ→Ｃ　３ｃｍ/ｓ
Ｑ；Ａ→Ｃ→Ｂ　５ｃｍ/ｓ
（１）①　62.0％
グラフをもとに答える。
ｙ＝ａｘ²
（１０、６００）の点を通るので、
６００＝１０²ａ
ａ＝６
（*１０秒後にＰはＢ、ＱはＣに同時について、
△ＡＰＱは△ＡＢＣの面積と等しくなります）

②記述式。　37.1％　部分正答含－50.7％
直線の式を求める。
傾きは、右に５、下に６００だから、
－６００/５＝－１２０
（１５、０）の点を通るので、
ｙ＝ａｘ＋ｂに代入して切片を求める。

（２）①　67.6％
数量変化の意味を読み取る。
１０秒後にＰはＢ、ＱはＣ→面積は△ＡＢＣ
１５秒後にＰとＱが辺ＢＣ上で出会い、△ＡＰＱはゼロ。
１８秒後は【ＱがＢにつく】。
なぜなら、１０秒後はＰ・Ｑともにゴールまで残り４０ｃｍなので、
Ｑの方が速いから、Ｑが先に着きます。　→　ウ
（*Ａ－Ｃ―Ｂ間が９０ｃｍだから、９０÷５＝１８秒）

②　37.7％
１８秒以降は、辺ＢＣ上のＰがＣに向かう途中。
１５～１８秒間はＰとＱが互いに離れていくので、
△ＡＰＱの底辺ＰＱは毎秒８ｃｍ伸びていく。
１８秒以降はＱが止まり、Ｐだけが動くので、
底辺ＰＱは毎秒３ｃｍしか伸びない。
変化の割合は、１５～１８秒より１８～秒の方が小さくなる。
傾きの緩いⅠが正しい。　→　ア

（３）　2.7％!!
Ⅰのグラフで500ｃｍ³あたりのところに横線をひいてみよう。
３度目に５００ｃｍ³となるのは、１８秒以降。
底辺をＡＢとすると、高さはＰＢ。
ＰＢ＝５００×２÷３０＝１００/３
Ｐが動く距離は、
３０＋１００/３＝１９０/３ｃｍ
Ｐは秒速３ｃｍなので、、
１９０/３÷３＝１９０/９秒後

大問６（条件文）

栃木数学の個性(p_-)
（１）　51.3％
ルールを理解しているかチェック！
〔４×４〕の正方形が１つ。
〔２×２〕の正方形が２つできます。
よって、２ｃｎ

（２）　10.0％！
縦がｎ、横が３ｎ＋１

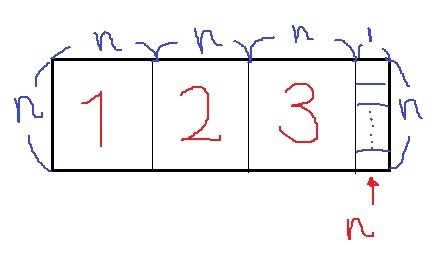
〔ｎ×ｎ〕が３つ。〔１×１〕がｎ個できる。
よって、ｎ＋３個

（３）　3.5％!!　部分正答含－6.7％！
ここも記述式。
これがイメージできれば一発↓

赤いところで2つの等式が得られる。ここから連立を組む。

（４）　0.5％!!!　部分正答含－1.4％！
満点をとらせない問題。
横が５６ｃｍ。３種類の正方形が５つできた。
サイズを大・中・小として、小の１辺をｘとおいてみよう。
↑この３つしかないはず。
大は必ず左に１つ。
大が３つ連ねると、残りが中・中となり、小が作れない。
だから、大の枚数は１～２枚。
あとは、小の１辺をｘとおいて、横の長さで５６を割り切れるよう、
正方形を縦や横にあっちこっち配置して、自力で探す。
長方形の縦の長さは、２１・３２・４０ｃｍとなる。
公立高校入試解説ページに戻る