2022年度　北海道公立高校入試問題過去問【数学】解説

受検者平均48.1点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　98.0％
８×（－４）
＝－32

②　90.0％
（－５）²－９÷３
＝25－３
＝22

③　89.2％
４√５＋√20
＝４√５＋２√５
＝６√５

（２）　84.3％
ａ²＋２ａｂ
＝７²＋２×７×（－３）
＝49－42
＝７

＠別解＠
ａ²＋２ａｂ
＝（ａ＋ｂ）²－ｂ²
＝（７－３）²－（－３）²
＝16－９＝７
大して時間は変わりません。

（３）　72.2％
ｙ＝－２ｘ＋８にｙ＝０を代入。
－２ｘ＋８＝０
ｘ＝４
Ａ（４、０）

（４）　69.4％
３ｘ－２ｙ＝－ｘ＋４ｙ＝５
３ｘ－２ｙ＝５　…①
－ｘ＋４ｙ＝５　…②
①×２＋②をすると、５ｘ＝15
ｘ＝３
②に代入、ｙ＝２
ｘ＝３、ｙ＝２

（５）　60.4％
『以下』だからｘ≦10

（６）　50.7％

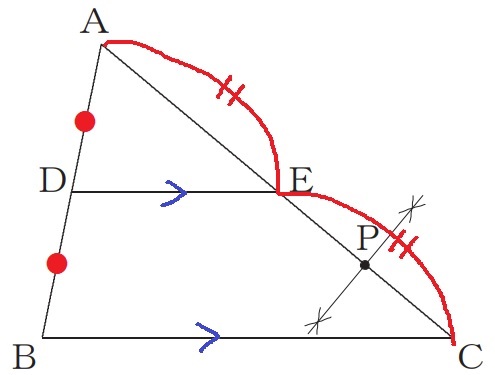
ＤＥ//ＢＣだから、ＡＤ：ＤＢ＝ＡＥ：ＥＣ＝１：１
ＥＣの中点がＰであれば、ＡＰ：ＰＣ＝３：１になる。
ＥＣの垂直二等分線をひき、ＡＣとの交点がＰ。

大問２（データの活用）

（１）①　66.3％

Ｂの第３四分位数（Ｑ3）は8.6秒。

②　74.3％
ア：範囲（レンジ）＝最大値－最小値。同じである。×
イ：四分位範囲＝第３四分位数（Ｑ3）－第１四分位数（Ｑ1）、Ａの方が大きい。〇
ウ：平均値は×印などで示されるが、本問の箱ひげ図には記載がない。×
エ：最大値はＢの方が大きい。×
イ

（２）　21.4％！
ア：15人の中央値は８番目の値。
８番目が7.4秒だから、7.5秒より速い人は少なくとも８人いる。
イ：８番目が7.6秒なので、7.5秒より速い人は最も多くて７人。
ウ：Ｂ組の方が7.5秒より速い人が多い。
ア…８、イ…７、ウ…Ｂ組

大問３（関数）

（１）　83.7％
ｙ＝ａｘ²に（ｘ、ｙ）＝（２、12）を代入。
12＝４ａ
ａ＝３

（２）①　15.4％！

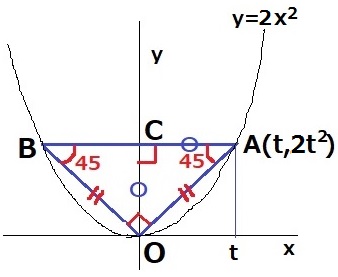
ａ＝２で試してみると、Ａ（ｔ、２ｔ²）
ＡＢはｘ軸に平行だから、ｙ軸を対称の軸として△ＯＡＢは左右対称→直角二等辺三角形。
ＡＢの中点をＣとすると、△ＯＣＡも直角二等辺→ＣＡ＝ＣＯでＡのｘ座標とｙ座標は等しい。
２ｔ²＝ｔ
ｔ＞０だから両辺をｔで割って、
２ｔ＝１
ｔ＝１/２

ａ＝１のとき、ｔ＝１
ａ＝２のとき、ｔ＝１/２
ａｔの積は１で一定である。
Ｘ…１/２、Ｙ…ウ、Ｚ…１

②　5.2％!!
説明問題。
この形式は他県でも見かけるが、説明で出されると書きづらい(´～`)

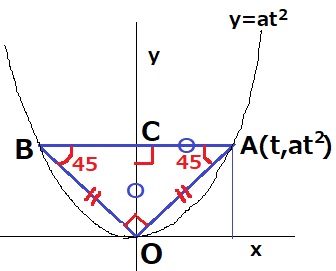
前問の処理をａで行う。
公式解答では△ＯＡＢと△ＯＡＣは直角二等辺であるとサラリと指摘して、
Ａ（ｔ、ａｔ²）より方程式を立てる→ａｔ＝１を導き、結論を記述している。

ａｔ²＝ｔの両辺をｔで割るときは、ｔ＞０の条件はつけておきたい。
方程式を文字で割るとき、ｔ＝０のときは割れないが（割る数が０はダメ）、
問題文では「ｔ＞０」とあるのでｔで割ることが許される。

大問４（平面図形）

（１）　70.0％

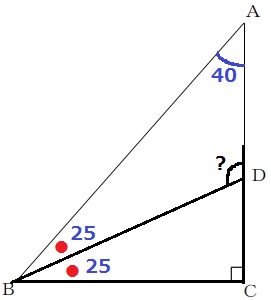
∠ＡＢＣ＝180－（40＋90）＝50°
∠ＤＢＣ＝50÷２＝25°
△ＢＣＤで外角定理→∠ＡＤＢ＝25＋90＝115°

（２）①　42.0％

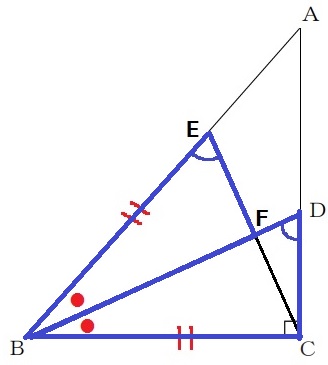
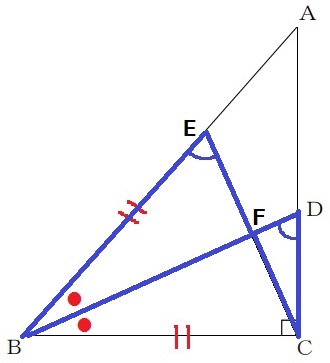
４点の同一円周上といえば、円周角定理の逆。
直線ＢＣについて同じ側にある∠ＢＥＣ＝∠ＢＤＣを指摘すればいい。
この２つの角が対応する三角形の相似を見つける。
∠ＥＢＦ＝∠ＤＢＣがわかっているので、△ＢＦＥ∽△ＢＣＤがやりやすい。
ア…ＢＤＣ、イ…ＢＦＥ、ウ…ＢＣＤ

＠余談＠

やや面倒ですけど…△ＢＦＥ∽△ＣＦＤでもいける。

②　8.5％!!
△ＢＦＥ∽△ＢＣＤ経由で、４点Ｂ、Ｃ、Ｄ、Ｅが同一円周上にあることを証明する。

ポイントは二等辺三角形。
二等辺三角形の頂角を２等分する直線は、底辺を垂直に２等分する。
これを指摘するだけで、∠ＢＦＥ＝90°が導ける。
仮定の∠ＥＢＦ＝∠ＤＢＣ、∠ＢＦＥ＝∠ＢＣＤの２角相等で△ＢＦＥ∽△ＢＣＤ

対応する角は等しいから、∠ＢＥＦ＝∠ＢＤＣ
２点Ｄ、Ｅが直線ＢＣについて同じ側にあり、∠ＢＥＣ＝∠ＢＤＣだから、
円周角定理の逆で４点Ｂ、Ｃ、Ｄ、Ｅは同一円周上にある。

大問５（平面図形・整数）

（１）①　65.5％
△ＣＡＯで三平方→４√３ｃｍ

②　11.8％！
ここも説明問題(´°ω°`;)
公式解答に即して解説する。

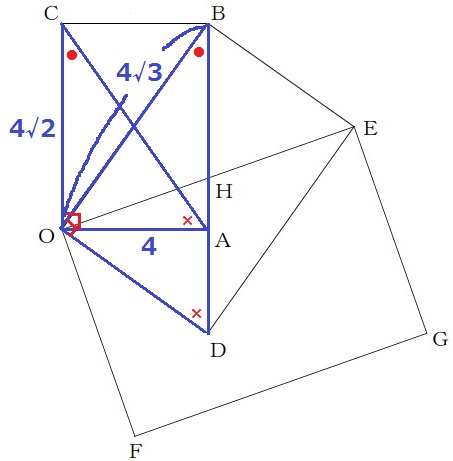
【ＯＤ：ＯＢ＝ＯＡ：ＯＣ】は、△ＯＢＤ∽△ＯＣＡから導ける。
長方形が相似なので、それらを対角線で２等分した２つの直角三角形も相似。
ＯＤ＝４√３×４/４√２＝２√６ｃｍ
△ＯＢＤで三平方→ＢＤ＝６√２ｃｍ

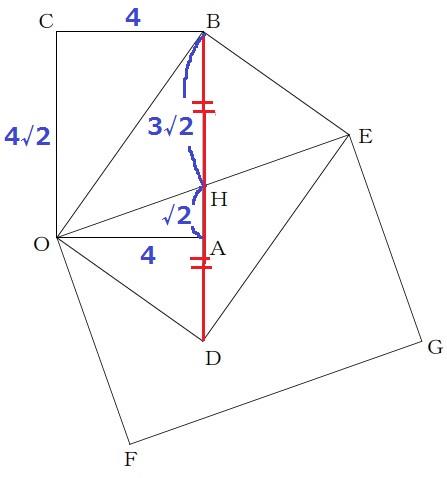
長方形の対角線はおのおのの中点で交わるので、ＢＨ＝６√２÷２＝３√２ｃｍ
ＡＨ＝ＡＢ－ＢＨ＝４√２－３√２＝√２ｃｍ
よって、△ＯＡＨの面積は、４×√２÷２＝２√２ｃｍ²

＠別解＠
他に抜け道がないか探ってみました。

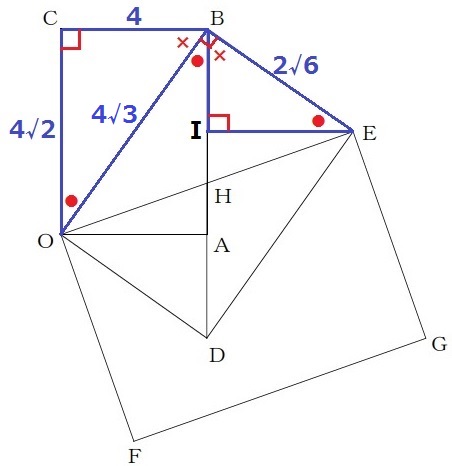
先のようにＢＥ＝２√６ｃｍまでは出す。
Ｅから垂線、足をＩとする。
●＋×＝90°の角度調査で、△ＢＣＯ∽△ＢＩＥ
△ＢＣＯの辺の比は、４：４√２：４√３＝１：√２：√３
ＢＩ＝２√２ｃｍ、ＩＥ＝４ｃｍ

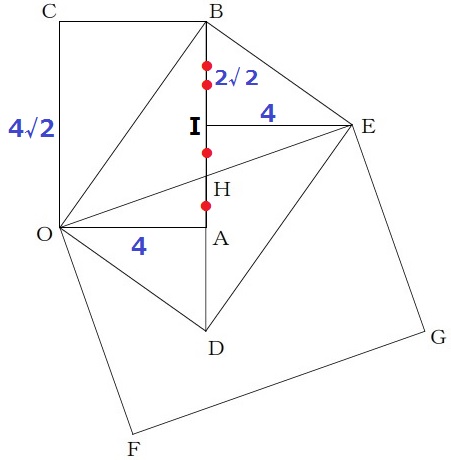
ＡＢ＝４√２ｃｍだから、ＩはＡＢの中点である。
△ＩＥＨ∽△ＡＯＨでＩＥ：ＡＯ＝１：１→ＨはＩＡの中点。
ＢＨ：ＨＡ＝３：１なので、△ＯＡＨの面積は、４×４√２×１/２×１/４＝２√２ｃｍ²

（２）① 4.0%!!
ここも答案に説明が要求される。
102を素因数分解すると、102＝２×３×17
根号の中が平方数になれば、根号の外のａの部分が作れる。
しかし、すべてを平方数にすると√ｂが作れない。
もっとも、２つのサイコロの出目の合計は最大でも12だから、
17は必ず根号の中に残る→２か３の素因数を持つ数がｎとなる。
ｎ＝２、３、４、６、８、９、10、12

②　6.3％!!
余事象の方が早い。
ｎ＝１→無し。
ｎ＝５→（１、４）（２、３）と逆
ｎ＝７→（１、６）（２、５）（３、４）と逆
ｎ＝11→（５、６）と逆
計12通り。
全体は６×６＝36通りだから、36－12＝24通り
確率は24/36＝２/３