2020年度　法政大学第二高校過去問【数学】大問５解説

問題ＰＤＦ
下の図のように長方形ＡＢＣＤと正方形ＡＢＦＥがある。円Ｏは正方形ＡＢＦＥに内接している。辺ＡＢ、辺ＤＣの中点をそれぞれＬ、Ｍとし、ＬＭとＥＦの交点をＮとする。円Ｏの周上に点Ｐをとり、直線ＬＰと辺ＥＤとの交点をＱとすると、ＰＮ//ＱＭとなった。ＡＥ＝４ｃｍ、ＥＤ＝２ｃｍであるとき、次の各問に答えなさい。

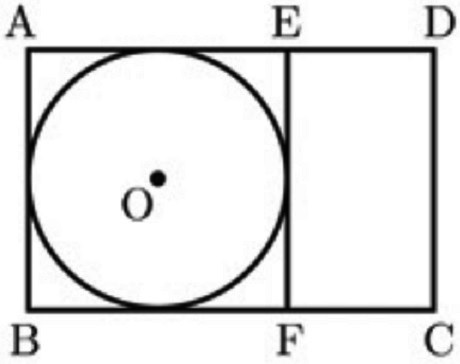
（１）
∠ＬＱＭの大きさを求めなさい。

（２）
面積比△ＬＱＭ：△ＭＤＱ：△ＱＡＬを分数を含まない形で表しなさい。

＠解説＠
（１）

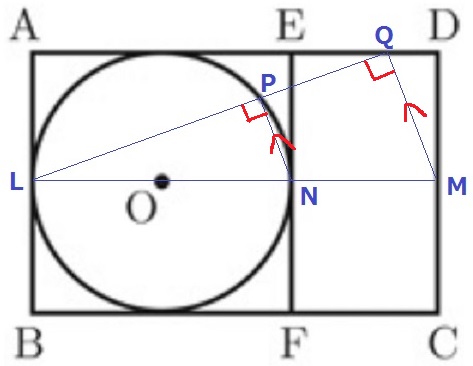
点の位置を図に記す。
半円の弧に対する円周角は直角→∠ＬＰＮ＝90°
ＰＮ//ＱＭから同位角が等しい→∠ＬＱＭ＝90°

（２）

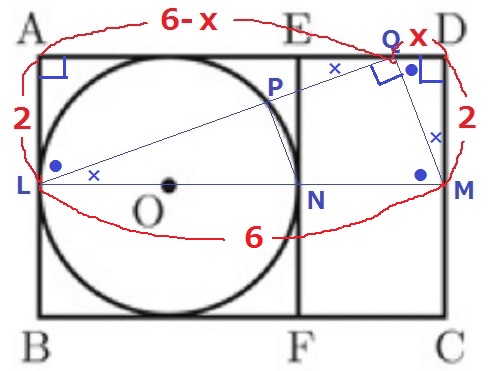
●＋×＝90°で角度を調べると、２角相等で△ＬＱＭ∽△ＭＤＱ∽△ＱＡＬ
ＱＤ＝ｘとおくと、ＡＱ＝６－ｘ
△ＭＤＱ：△ＱＡＬより、ＭＤ：ＤＱ＝ＱＡ：ＡＬ
２：ｘ＝６－ｘ：２
内項と外項の積で、６ｘ－ｘ²＝４
ｘ²－６ｘ＋４＝０
解の公式を適用。ｘの係数が偶数なのでｂ＝２ｂ’が使える。
ｘ＝３±√５
ＥＤ＝２ｃｍでＱは辺ＥＤ上の点だから０＜ｘ＜２→ｘ＝３－√５
ＡＱ＝６－（３－√５）＝３＋√５

△ＬＱＭと△ＭＤＱと△ＱＡＬは高さ２ｃｍで一定なので、底辺の比がそのまま面積比になる。
△ＬＱＭ：△ＭＤＱ：△ＱＡＬ＝ＬＭ：ＱＤ：ＡＱ＝６：３－√５：３＋√５
国私立高校入試解説ページに戻る