問題ＰＤＦ
ｎを１より大きい整数とし、１からｎまでの整数を１つずつ書いたｎ枚のカードがある。これらｎ枚のカードをよく混ぜて、左から順に横一列に並べてできるｎ桁の数をＡとする。このＡについて、以下の【操作】を行う。次の図１から図３は、ｎ＝４でＡが3421の場合について、それぞれの【操作】１から３を表している。
今、Ａに【操作】を繰り返し行い、一番左に書かれた数が１になったところで【操作】を終了する。また【操作】が終わるまでの回数をＮ（Ａ）とする。ただし、Ａの一番左の数が１であるときは【操作】を行わず、Ｎ（Ａ）＝０とする。
例えば、ｎ＝４として、Ａが3421の場合、【操作】を繰り返し行うと3421→2431→4231→1324となり、Ｎ（3421）＝３である。
次の各問に答えよ。
〔問１〕
Ｎ（31452）の値を求めよ。
〔問２〕
ｎ＝４とする。ａ、ｂ、ｃ、ｄは互いに異なる整数で１、２、３、４のいずれかとする。
以下の等式①、②、③が同時に成り立つとき、ａ、ｂ、ｃ、ｄの値を求めよ。
ただし、答えだけでなく、答えを求める過程が分かるように、途中の式や考え方なども書け。
①Ｎ（ａｂｃｄ）＋Ｎ（ｂｃｄａ）＝Ｎ（ａｂｃｄ）
②Ｎ（ａｂｃｄ）×Ｎ（ｃａｄｂ）＝Ｎ（ａｂｃｄ）
③Ｎ（ａｂｃｄ）＝４
〔問３〕
ｎ＝５でＮ（Ａ）≧１とする。
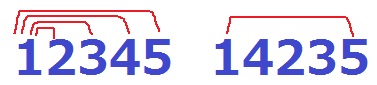
Ａに行った【操作】が終了したときの数を調べたところ、12345や14235などは存在した。しかしどんなＡで【操作】を行っても、【操作】が終了したときの数で、例えば、13254は存在しなかった。全てのＡについて【操作】が終了したときに存在しなかった数を調べたところ、13254も含めて全部で９個の数があることが分かった。
これら９個の数の中で３番目に大きい数を求めよ。
＠解説＠
問１
操作を確認する。
一番左に書かれてある数の枚数分、左から取り出して順番を左右入れ替える。
31452→（左３桁を入れ替える）→41352→（左４桁を入れ替える）→53142…
→24135→42135→31245→21345→12345
操作は７回だから、Ｎ（31452）＝７
問２
西らしい変化球のある問題( ;ﾟ∀ﾟ)
分かってしまえば単純なので、臆することなく挑みたい。
①Ｎ（ａｂｃｄ）＋Ｎ（ｂｃｄａ）＝Ｎ（ａｂｃｄ）
両辺からＮ（ａｂｃｄ）を引く。
Ｎ（ｂｃｄａ）＝０
値が０ということは操作をしないので、左端のｂは１である。
②Ｎ（ａｂｃｄ）×Ｎ（ｃａｄｂ）＝Ｎ（ａｂｃｄ）
両辺をＮ（ａｂｃｄ）で割る。
Ｎ（ｃａｄｂ）＝１
ｃａｄ１から操作１回で終了するので、ｃ＝４が確定。
③Ｎ（ａｂｃｄ）＝４
操作回数は４回。
ａ１４ｄでａ＝２だと操作が１回で終わってしまうから不適。
ａ＝３、ｄ＝２
3142→4132→2314→3214→1234◎
ａ＝３、ｂ＝１、ｃ＝４、ｄ＝２
＠＠
書き方は公式解答を倣ってください。
問３
操作終了時にありえない数字が９個あり、そのうち３番目に大きい数を求める。
手順を逆にして、操作終了直前の数字を考える。
12345は12をひっくり返して21345、123をひっくり返して32145。
同様に左４桁を逆にして43215、左５桁（全部）を逆にして54321が可能性として挙げられる。
14235は53241でありうる。
左端からの距離と番号が一致すると、その数は存在する。
最も大きい15432はありえない。〇
次点の15423もありえない。〇
15342は左３桁と左４桁がありえる。×
15324は左３桁で×。15243は左４桁で×。
15234はありえない。〇
３番目に大きいのは15234。
国私立高校入試解説ページに戻る
コメント