2020年度　市川高校過去問【数学】大問３解説

問題ＰＤＦ
１辺の長さが１の立方体を積み重ねて直方体を作り、
この直方体に含まれる様々な大きさの立方体の個数について考える。

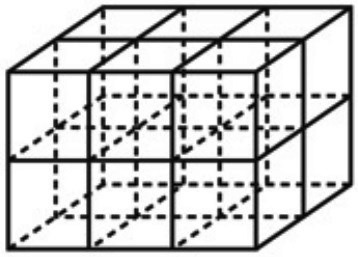
例えば、上の図のような、３辺の長さがそれぞれ２、３、２の直方体に含まれる立方体の個数は、１辺の長さが１の立方体が12個、１辺の長さが２の立方体が２個、１辺の長さが３以上の立方体が０個であるから、全部で14個である。
（１）
３辺の長さがそれぞれｎ、ｎ、４の直方体について、次の問いに答えよ。
ただし、ｎは４以上の自然数とする。
①この直方体に含まれる１辺の長さが２の立方体の個数をｎを用いて表せ。
②この直方体に含まれる様々な大きさの立方体の個数が全部で500個であるとき、ｎの値を求めよ。

（２）
一般に、ｎが自然数のとき、

が成り立つことが分かっている。
例えば、ｎ＝５のとき、
である。
ここで、３辺の長さがそれぞれｎ、ｎ、ｎの立方体について、この立方体に含まれる様々な大きさの立方体の個数が全部で44100個であるとき、ｎの値を求めよ。

＠解説＠
（１）①

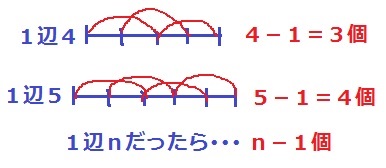
１辺が４のとき、隣り合う２つのペアは３個。
式で書けば、４－１＝３個

②
直方体の１辺の長さが４ということは、立方体の１辺の長さは１～４の範囲。
◆立方体の１辺が１
立方体の個数は、ｎ×ｎ×４＝４ｎ²個

◆立方体の１辺が２
前問より、３（ｎ－１）²個

◆立方体の１辺が３
前問と同様に考える。

今度は－１ではなく、－２になる！
（ｎ－２）×（ｎ－２）×２＝2（ｎ－２）²個

◆立方体の１辺が４
今までの流れから－３。
（ｎ－３）×（ｎ－３）×１＝（ｎ－３）²個

４ｎ²＋３（ｎ－１）²＋２（ｎ－２）²＋（ｎ－３）²
＝４ｎ²＋３ｎ²－６ｎ＋３＋２ｎ²－８ｎ＋８＋ｎ²－６ｎ＋９
＝10ｎ²－20ｎ＋20＝500
10ｎ²－20ｎ－480＝０　_{←すべてを÷10}
ｎ²－２ｎ－48＝（ｎ－８）（ｎ＋６）＝０
ｎ＞０ゆえ、ｎ＝８
８個

（２）
今度はどの辺の長さもｎである立方体。
今までの規則を利用しよう(ﾉ)`ω´(ヾ)

１辺が１→ｎ³
１辺が２→（ｎ－１）³
１辺が３→（ｎ－２）³
…
１辺がｎ－２→３³
１辺がｎ－１→２³
１辺がｎ→１³
１³＋２³＋３³･･･＋（ｎ－２）³＋（ｎ－１）³＋ｎ³＝44100

ここで問題文で提供された公式にあてはめる。
｛１/２×ｎ×（ｎ＋１）｝²＝44100＝441×100＝21²×10²＝210²
１/２ｎ（ｎ＋１）＝210　_{←両辺２倍}
ｎ²＋ｎ＝ｎ（ｎ＋１）＝420
連続する２数の積が420→20×21＝420
ｎ＝20

＠総和を求める公式＠
１乗和の公式（１＋２＋･･･ｎ）＝ｎ（ｎ＋１）/２
２乗和の公式（１×１＋２×２･･･ｎ×ｎ）＝ｎ（ｎ＋１）（２ｎ＋１）/６

２乗和は高校数学で習いますが、浅野中学で求め方が出題されたのでそちらを参照してください。

2019年度　浅野中学過去問【算数】大問２解説

問題ＰＤＦ 次の文章を読み、〔　ア　〕～〔　オ　〕にあてはまる数をそれぞれ答えなさい。 　Ａ君は、〔図３〕のような２枚の長方形の紙を利用して、１から20までの和を求めたところ、１＋２＋３＋･･･＋20＝〔　ア　〕となりました。 さらにＡ君は...

sabotensabo.com

2019.04.18

３乗和の公式（1×1×1＋2×2×2＋ｎ×ｎ×ｎ）＝{ｎ（ｎ＋１）/２}²
３乗和は１乗和の値を２回かけるだけで出せてしまう。
（ex.１～20までの３乗和の場合。１～20の１乗和が210だから、３乗和は210×210＝44100）
３乗和でも幾何的な発想で公式を導くことができます。
詳しくはコチラ→ロボット・ＩＴ雑食日記

３乗和が１乗和の２乗。
２乗ということは正方形の面積で考える。
１×１×１が青の正方形。
２×２×２は２×２の正方形が２つあり、１つを半分にわけてくっつけると、
青＋緑の正方形の面積となる。
３×３×３は３×３の正方形を３つくっつける（オレンジ）。
４×４×４は４×４の正方形が４つあり、１つを半分にわけてくっつける（赤）。

全体の正方形をみると、１辺が１の正方形、１＋２の正方形、１＋２＋３の正方形、１＋２＋３＋４の正方形…と広がっていくので、３乗和は１乗和の２乗となる。
国私立高校入試解説ページに戻る