問題ＰＤＦ
図のように、△ＡＢＣの内接円の中心をＯとし、
円Ｏと辺ＡＢ、ＢＣ、ＣＡとの接点をそれぞれＤ、Ｅ、Ｆとする。
３点Ｅ、Ｏ、Ｄを通る円をＰとする。
（１）
円Ｐは点Ｂを通ることを証明せよ。
同様に、３点Ｅ、Ｏ、Ｆを通る円とＱとすると、円Ｑは点Ｃを通る。
図のように、直線ＦＤと円Ｐの交点をＧ、直線ＧＥと円Ｑの交点をＨ、
直線ＨＦと円Ｏの交点をＩとする。
（２）
∠ＢＥＧ＝∠ＦＩＤを示し、△ＦＤＩは二等辺三角形であることを証明せよ。
＠解説＠
（１）
円Ｏと円Ｐだけを見る。Ｇの情報も不要。
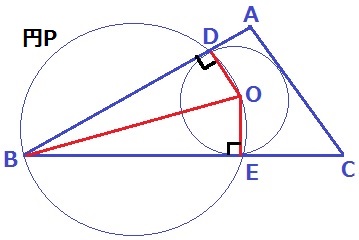
↑内接円といえばこの形。
半径ＯＤ、ＯＥはそれぞれ接線ＢＡ、ＢＣに対して垂直に交わる。
∠ＯＤＢ＋∠ＯＥＢ＝180°だから、四角形ＢＥＯＤは円に内接するので、
４点Ｂ、Ｅ、Ｏ、Ｄは同一円周上にある。
したがって、円Ｐは点Ｂを通る。
＠４点が同一円周上にある証明＠
①円周角定理の逆
公立高校入試でも頻出。
同じ円であれば、同じ弧に対する円周角が等しい。
⇒同じ弧に対する円周角が等しければ、同じ円。
『直線〇〇に対して同じ側にある２点〇、〇について、
∠〇〇〇＝∠〇〇〇が成り立つとき、４点〇〇〇〇は同一円周上にある』
この言い回しは証明で書けるようにしておきたい。
②内接四角形の性質
・対角の和が180°である。
・外角はそれと隣り合う内角の対角に等しい。
どちらかを指摘すれｂば、同一円周上の点にあるといえる。
③方べきの定理の逆
受験の月より。
方べきの定理から、ＰＡ・ＰＢ＝ＰＣ・ＰＤが成り立つ。
逆にＰＡ・ＰＢ＝ＰＣ・ＰＤが成り立てば、４点は同一円周上にある。
（２）
Ｉが厄介な位置にある。
弧ＤＦ、弧ＦＩの円周角が使えにくい。
円ＯはＤでＡＢと接している⇒接弦定理に思考を変える。
∠ＢＥＧから出発して時計回りに移動していくと、、
∠ＢＥＧ⇒弧ＢＧに対する円周角⇒対頂角⇒接弦定理⇒∠ＦＩＤ
∠ＢＥＧ＝∠ＦＩＤ …①
後半も同様。円ＯはＦでＡＣと接している。
今度は反時計回りに進んで、、
∠ＢＥＧ⇒対頂角⇒弧ＨＣに対する円周角⇒接弦定理⇒∠ＦＤＩ
∠ＢＥＧ＝∠ＦＤＩ …②
①、②より∠ＦＩＤ＝∠ＦＤＩ
△ＦＤＩは２つの底角が等しく、二等辺三角形である。
国私立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント